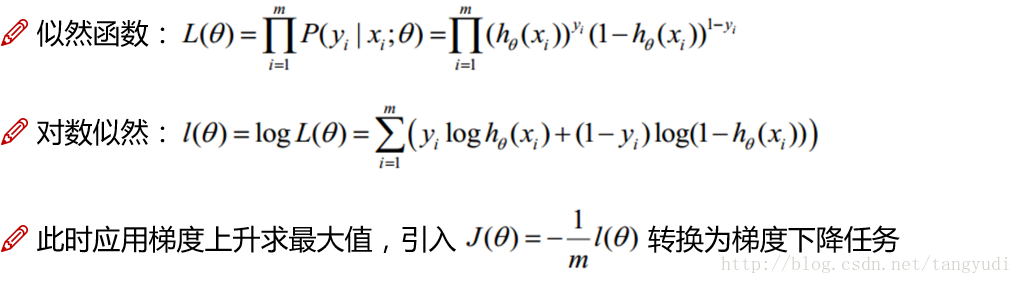一. 线性回归 VS 逻辑回归
线性回归,一般处理因变量是数值型区间变量(连续),用来拟合因变量和自变量之间的线性关系,但是因变量和自变量都是连续区间,常见的线性模型:
而在分析实际问题时,所研究问题变量不仅有区间变量(连续变量),也有属性变量(分类变量 or 顺序变量),如二项分布问题,通过分析患者的年龄、性别、体质指数、平均血压、疾病指数等指标,判断一个人是否有糖尿病,Y = 0表未患病,Y = 1表患病,这里的响应变量(分类变量)是一个两点(0-1)分布变量,它不能用h函数处理因变量是连续变量的问题,若因变量是定性(分类)问题,线性回归model就不能解决这个问题了,需要采用逻辑回归来解决定性(分类)问题。
逻辑回归,用来处理因变量为分类变量的回归问题,因为与回归问题非常相似,仅仅是输出不一样,所以称为逻辑回归(逻辑回归用了和回归类似的方法来解决了分类问题),常见的是二分类问题,它也能处理多分类问题,逻辑回归实质是一种分类问题。
In short: 输出变量类型是连续时,为线性回归(目标函数 均方误差和),输出变量类型是离散时,为逻辑回归(分类),目标函数(通常有正则项)
二. 逻辑回归 逻辑回归是一个非线性二分类(多分类)问题
对于一个逻辑回归问题(二分类问题),针对一个具体样本,我们不仅仅想知道这个样本属于哪一类,同时还想知道属于概率的概率是多大。对于线性回归和非线性回归的分类问题都不能回答这个问题,因为线性回归和非线性回归的为题,都是假设其分类函数如下: Y = W * X + b,因为Y的取值范围是(负无穷大,正无穷大),Y不能很好的给出属于某一类的概率(概率的取值范围[ 0 , 1 ]),所以我们需要一个更好的映射函数,不仅可以将分类结果很好的映射到 [ 0, 1 ]之间的概率,同时这个函数也应该有很好的可微分性;这个映射函数为逻辑斯谛函数(又称 sigmoid函数),其表达式如下:
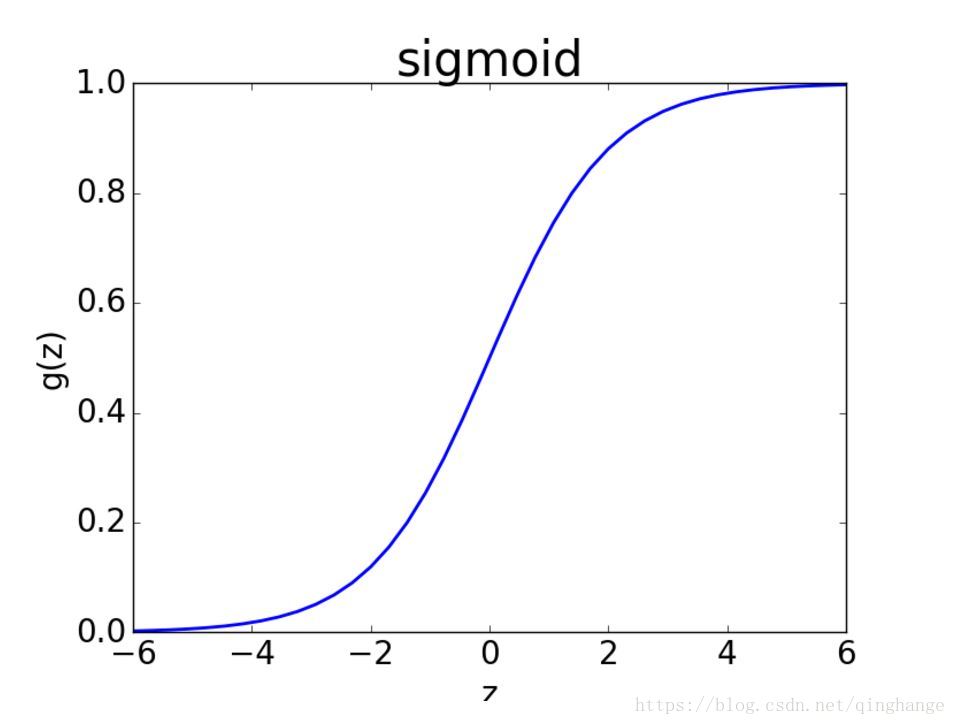
Sigmoid函数图像如下:
sigmoid函数完美的解决了上述需求,同时sigmoid函数连续可微
作用:将任意的输入映射到[ 0, 1 ]区间,线性回归中得到一个预测值,then通过sigmoid函数映射到[ 0, 1],实现值到分类概率的转化
假设数据离散二类可分,分为0类和1类;当z值大于0的时候,sigmoid的概率大于1/2,表明偏向于类别1;反之则偏向于类别0。
阈值的选择:
在没有任何先验条件的情况下,这里的阈值一般选择0.5。但当我们有进一步明确需求的时候,阈值也是可以调整的,例如我们希望对正例样本有更高的准确率要求,则可以把阈值适当地调高,例如调高到0.6;相反,假如我们希望对正例样本的召回率要求更高,则可以把阈值适当地降低,例如降低到0.4;
3. 参数估计---损失函数(Loss Function)和成本函数(Cost Function)
在二类分类中,假设sigmoid输出结果表示属于第 1 类的概率值,用的是均方损失函数
φ(z(i))表示sigmoid对第i个值的预测结果,我们将sigmoid函数带入上述成本函数中,绘制其图像,发现这个成本函数的函数图像是一个非凸函数,如下图所示,这个函数里面有很多极小值,如果采用梯度下降法,则会导致陷入局部最优解中,有没有一个凸函数的成本函数呢?

假设sigmoid函数φ(z)表示属于1类的概率,于是做出如下的定义:

将两个式子综合来,可以改写为下式:

上式将分类为0和分类和1的概率计算公式合二为一。假设分类器分类足够准确,此时对于一个样本,如果它是属于1类,分类器求出的属于1类的概率应该尽可能大,即p(y=1lx)尽可能接近1;如果它是0类,分类器求出的属于0类的概率应该尽可能大,即p(y=0lx)尽可能接近1。
4. 参数估计---极大似然法求解逻辑回归
借助极大似然法估计参数w和b,对数似然函数并整理:
对于逻辑回归的求解,已然沿用我们上次跟大家讨论的梯度下降算法。给出似然函数,转换对数似然(跟线性回归一致),但是我们现在的优化目标却跟之前不太一样了,线性回归的时候我们要求解的是最小值(最小二乘法),但是现在我们想得到的却是使得该事件发生得最大值,为了沿用梯度下降来求解,可以做一个简单的转换添加一个负号以及一个常数很简单的两步就可以把原始问题依然转换成梯度下降可以求解的问题。

逻辑回归是一个二分类算法,那如果我的实际问题是一个多分类该怎么办呢?这个时候就需要Softmax啦,引入了归一化机制,来将得分值映射成概率值。
reference:
第一段参考及调参: https://blog.csdn.net/liulina603/article/details/78676723
代码及扩展: https://blog.csdn.net/lc013/article/details/55002463
LR流程解析及推导: https://blog.csdn.net/tangyudi/article/details/80131307
LR思路及推导: https://blog.csdn.net/zjuPeco/article/details/77165974
手推LR : https://blog.csdn.net/hzw19920329/article/details/77281986