LMS自适应滤波的FPGA实现(一)
真的是准备电赛到不知道还要准备什么了 著
可以选择文末点个赞

本文较长,建议使用电脑端+简书目录配置使用
原理-最优估计技术
这一部分是建议大家看完后面的在跳回来.
术语/模型定义和基本假设
在立论之前,我们先定义一下相关信号量和系统模型,这次的系统大概是这个样子的:
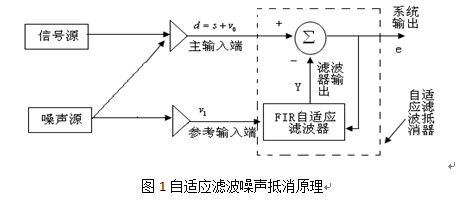
有几个会反复提及到的参量:
x=自适应系统的输入
y=自适应系统 的输出
d=(自适应系统的)期望响应
e=d-y=估计误差
而且我们在这里还需要对信号的特性进行假设,我们假设信号是满足广义稳态(Wide Sense Stationary)的.并不需要严格平稳或者是各态历经.也就是说信号具有一下特性:
对均值有:
η=Ex=N→∞limN1N=0∑N−1x[n]
对方差有:
σ2=E(x−n)2=N1N=0∑N−1(x[n]−η)2
对自相关函数:
r[τ]=Ex[t1]x[t2]=Ex[t+τ]x[t]=N→∞limN1N=0∑N−1x[n]x[n+τ]
特别地:
r[0]=Ex[t]x[t]=E{∣x[t]∣2}
代价函数
这个又是现在机器学习er喜见乐闻的定义了,
我们在这里定义误差函数为: $ e[n]=d[n]-y[n] $
其中d[n]是要估计的随机变量,y[n]是通过自适应滤波计算的估计点
我们在里用最小均方(也称最小二乘法)(也称平方误差代价函数)来定义代价函数:
J=E{e2[n]}=(d[n]−y[n])2
最优维纳估计
这里推导的目的在于如何从理论上得到最佳的h[k] (下称
fk)
假设我们使用FIR滤波器来解决问题,则输出的响应为:
y[n]=k=0∑L−1fkx[n−k]
不妨使用向量来表达上式:
y[n]=xT
[n]f
=fTx
[n]
所以我们可以更新e[n]:
e[n]=d[n]−y[n]=d[n]−fTx
[n]
进着,我们可以求解代价函数:
J=E{e2[n]}=E{d[n]−y[n]}2=E{d[n]−fTx
[n]}2=E{(d[n]−fTx
[n])(d[n]−fxT
[n])}=E{d[n]2−2d[n]fTx
[n]+fT
x[n]xT[n]f
}
在latex写向量是在太麻烦了,下省
大家可以回想一下梯度下降法,后面才会真正介绍,这里想进一步减少代价函数的话,只要对
f求偏导就可以了
∇=∂fT∂J=E{−2d[n]x[n]+2x[n]xT[n]fopt}=0
假设滤波器的权重向量f和信号向量x[n]是不相关的,则有:
E{d[n]x[n]}=E{x[n]xT[n]}fopt
所以结果就呼之欲出了:
fopt
=E{x
[n]xT
[n]}−1E{d[n]x
[n]}
一定要注意这里的x[n]是一个列向量,列向量,列向量
所以其实结果已经非常明显了,下面还是分开讲讲:
-
E{x
[n]xT
[n]}
很显然这个就是自相关矩阵,其中的矩阵形式是这样的:
⎣⎢⎢⎢⎡x[n]x[n]x[n−1]x[n]⋮x[n−(L−1)]x[n]x[n]x[n−1]x[n−1]x[n−1]⋯⋯⋯⋱⋯x[n]x[n−(L−1)]⋮⎦⎥⎥⎥⎤
=
⎣⎢⎢⎢⎡r[0]r[1]⋮r[L−1]r[1]r[0]r[L−2]⋯⋯⋱⋯r[L−1]r[L−2]⋮r[0]⎦⎥⎥⎥⎤
- $ E{ d[n]\vec{x}[n] }$
这里因为d[n]是一个标量,所以这个矩阵就是一个互相关函数的列向量而已
所以我们可以将f改写成:
fopt=Rxx
−1rdx
从公式我们可以看到,如果
fopt存在的一个前提在于,
Rxx的逆必须存在,也就是说
Rxx必须是非奇异矩阵,所以这才是我们前提所假设的广义平稳需要,因为对于广义平稳信号来说,他的
Rxx就是一个非奇异矩阵,并且存在逆矩阵
回代到代价函数,我们可以得到估计的标准误差,这里不给出过程了(懒)
Jopt=rdd[0]−foptTrdx
实践-维纳-霍夫算法
也就是上面所说的算法,现在我们假设输入是一个由曼彻斯特编码的信号m[n],幅值B=10,外加两个噪声:
- 高斯白噪声5dbm吧 2. 电力线噪声,幅值A=50 频率60Hz
现假设采样频率是电网噪声的4倍,即240Hz,我们用一个二抽头的FIR滤波器来解决这个问题
所以现在的d[n]为:
d[n]=Acos[πn/2]+Bm[n]+σ2n[n]
自适应滤波的输入的基准信号x[n]为:
x[n]=cos[nπ/2+ϕ]
其中
ϕ=π/6是一个角度偏移量.所以系统的输出是:
y[n]=f0cos[nπ/2+ϕ]+f1cos[(n−1)π/2+ϕ]
所以:
对于自相关函数:
rxx[0]=E{(cos[nπ/2+ϕ])2}=21
rxx[1]=E{cos[nπ/2+ϕ]sin[nπ/2+ϕ]}=0
对于互相关函数:
rdx[0]=E{(Acos[πn/2]+Bm[n]+σ2n[n])cos[nπ/2+ϕ]}=2Acos(ϕ)=12.53
rdx[1]=E{(Acos[πn/2]+Bm[n]+σ2n[n])sin[nπ/2+ϕ]}=2Acos(ϕ−π)=12.5
所以下矩阵为:
fopt=Rxx
−1rdx
=[rxx[0]rxx[1]rxx[1]rxx[0]]−1[rdx[0]rdx[1]]=[2002]−1[12.53
12.5]=[2002][12.53
12.5]=[253
25]
matlab仿真结果
现在给出matlab仿真结果:
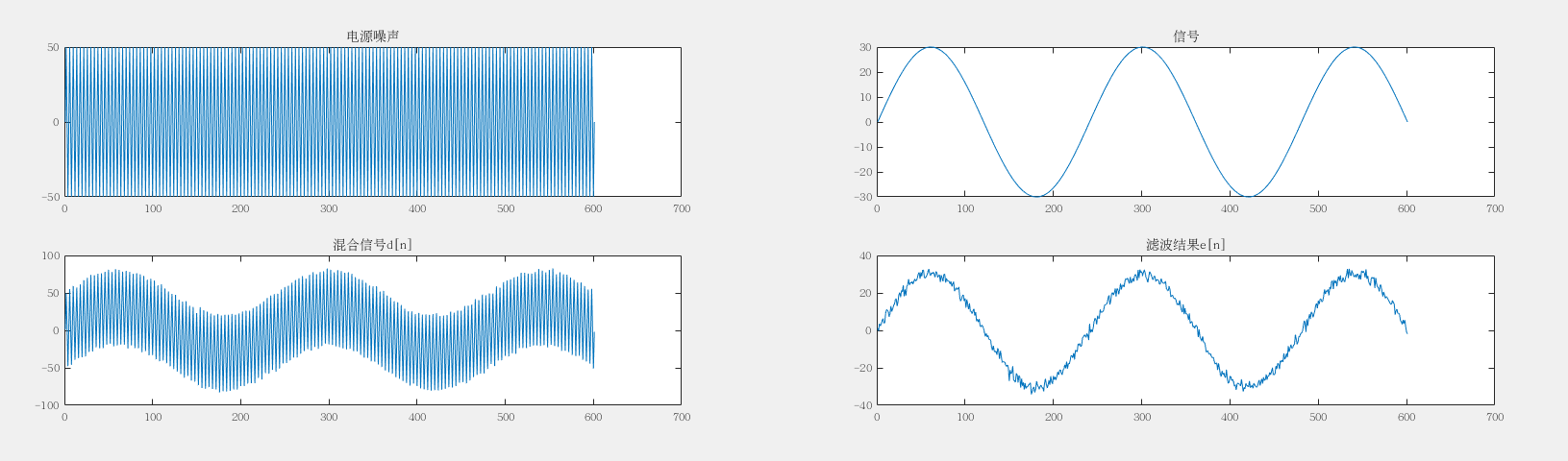
源码可联系作者获取
Widrow-Hoff最小二乘算法
从上面的最优维纳估计我们可以知道,实际上这种方法是理论不可实现的,因为自相关矩阵当系统规模变大的时候后变得极其的庞大和冗余,而且计算时间也极其长,所以我们需要一种方法来得到新的
Rxx−1
Widrow-Hoff最小二乘(LMS)算法是一种实时近似逼近
Rxx−1的实用方法,而且在后面的讨论中我们会发现他有较好的性能.而且公式极其对机器学习有基础的同学友好.
原理推导
实际上我们可以放弃对
fopt一次性求解,进而变成逐次按梯度逼近,也就是:
f[n+1]=f[n]−2μ∇[n]
这条公式相信学过梯度下降的同学都很熟吧…
所以现在我们对误差的估计就变成了对误差方向的估计,而用梯度下降的思想来考虑这个问题的话,我们就需要让误差的均值向每一个
f进行求导,即:
∇[n]=[∂f0∂E{e[n]2}∂f1∂E{e[n]2}⋯∂fL−1∂E{e[n]2}]T
实际上我们总不可能在FPGA上算误差的均值吧,所以这里要取真的误差值作为估计值:
∇^[n]=[∂f0∂e[n]2∂f1∂e[n]2⋯∂fL−1∂e[n]2]T=2e[n][∂f0∂e[n]∂f1∂e[n]⋯∂fL−1∂e[n]]T
所以实际上:
∇^[n]=−2e[n]∂f
∂e[n]=−2e[n]x[n]
回代到最初的起点,得:
f[n+1]=f[n]−μe[n]x[n]
请记住,这条是最为重要的公式.
参数限定
这里唯一要注意的参数就是这个每次迭代的
μ,在这里我们不展开,大家学过机器学习的可以迁移思考一下梯度下降的学习率(learning rate)过大或者过小对算法的影响
最后的一些碎碎念
实际上这篇博客我是不太想写的,因为其实这个工作是大二上学期的时候做的了.但是最近看机器学习的时候看到梯度下降的时候想了一下,还是决定写一下.
其实如果大家有修过高等代数或者吴恩达的机器学习的话,实际上你可以看到,前半部分的最优估计技术其实就是正规方程法,后半部分的Widrow-Hoff最小二乘算法就是通用的梯度下降法
再者,如果大家有修过凸优化理论的内点法的话,其实这个就是内点法里面的牛顿法…
结语
这就是我们要用FPGA实现的算法了,其实算法已经写完很久了,但是因为最近电赛的原因就重写一次吧…
但是因为这篇博客的公式实在是太多了,我都不好意思再写FPGA的结构设计了,就留待明天更新吧.
参考文献
高斯白噪声的产生
latex画矩阵
LMS算法自适应滤波器
自适应滤波器及LMS自适应算法的理解
通信原理教程(第三版) --樊昌信著
数字信号处理的FPGA实现
想我尽早更新的方法之一