深度学习笔记—线性回归（基础）

线性回归

在深度学习的基础学习阶段总是逃不过几个经典的实战问题，其中之一就是线性回归的经典数据集：Boston房价预测。
要解决这个问题我们需要用到一种很常见的机器学习算法：线性回归，使用线性回归解决问题之前，我们要搞清楚什么是线性回归，线性回归有什么用，怎么用线性回归去解决Boston房价预测问题。

1. 什么是线性回归

让我们看一看数学上对回归的定义：回归，指研究一组随机变量(Y1 ，Y2 ，…，Yi)和另一组(X1，X2，…，Xk)变量之间关系的统计分析方法，又称多重回归分析。通常Y1，Y2，…，Yi是因变量，X1、X2，…，Xk是自变量。（摘自百度百科）
简单来说回归是指一组随机因变量和另一组随机自变量之间的关系，这个定义很像函数中的定义，但明显其范围要广于函数，数学上将回归分为四类，分别是： 线性回归、曲线回归、二元logistic回归、多元logistic回归。
在Boston房价预测问题中，我们要使用的就是线性回归，所以什么是线性回归？线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w’x+e，e为误差服从均值为0的正态分布。看到这个表达式我们就很熟悉了，这个表达形式很像数学中的一元函数表达式，如果已知函数表达式，根据表达式我们可以求出任意x位置的y值，换个说法就是，我们可以预测出任意x位置的y值，到这里我们就可以明白如何利用线性回归进行预测了，我们需要求出线性回归方程，根据线性回归方程进行预测。

2. 如何理解线性回归

Boston房价分析的数据集很复杂有CRIM, ZN ,INDUS ,CHAS,NOX,RM,AGE,DIS,RAD,TAX,PTRATIO,LSTAT,MEDV等多个自变量，让人看的无从下手，所以我们先从一个简单的数据集看起，该数据集值规格为100 x 2 100行两列，第一列为自变量，第二列为因变量数据如图所示：（文末可下载该数据集）
单独看数据我们看不出来什么，但是我们可以将数据放在平面直角坐标系中，可以更直观的看出数据之间的关系，代码如下

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#reviews = pd.read_csv('./data/data.csv')
reviews = np.genfromtxt("./data/data.csv", delimiter=",")#delimiter 分割符号
fig, ax = plt.subplots()
ax.scatter(reviews[:,0], reviews[:,1])
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()

根据代码可以做出散点图：

通过图像我们可以直观的看到数据虽然不规律，但是在某种程度上在集中于两条直线之间，根据线性回归定义，我们需要找出来一条线，最大程度的经过这些点，如下图所示：

除去上下两侧边缘的直线外，其他的直线的拟合效果好像都不错，但是究竟什么直线的拟合效果最好呢，我们这里就需要引入一个度量拟合度好不好的概念：损失函数

什么是损失函数

简单来说损失函数就是衡量模型输出和真实标签之间的差距，模型就是我们上图画出的诸多直线 ，一条直线就叫一个模型，同一个x值在不同模型中对应不同y值，而标签就是给定数据集中与因变量对应的自变量的值，我们称之为标签集。

怎么计算损失

我们知道了用什么度量模型的拟合效果，但是我们该怎么利用损失函数这个工具呢，在上图中，我们将直线和数据放在同一个直角坐标系中，所有的数据点要么是在直线上，要么是在直线外，那么我们就可以计算所有的点到直线的距离和，使这个距离和越小越好，越小说明落在直线上的点越多，模型越精确，预测值自然就接近真实值。所以我们可以推出如下损失计算公式：

其中Y是标签，而f(x)则是根据模型计算输出的预测值这样看不是很直接，我们将公式展开如下

根据公式我们可以看出，在线性回归的损失计算中，就是求出每个模型给出的输出和标签的差距。所以我们的目标函数很清晰，就是让loss尽可能的小即预测值无限逼近真实值，我们观察上图的公式，loss函数只与w参数和b参数有关，所以我们只需要关注w和b，使loss值尽可能的小，so，我们该怎么求解合适的w和b参数呢，在模型的建立过程中，w和b不可能一步到位，我们只能利用Gradient Descent（梯度下降）一步一步的去更新w和b参数，使损失降到最小。

Gradient Descent

梯度下降法，简单来说就是根据梯度找函数的最低点，梯度是一个由所有的轴方向的偏微分组成的向量，大小是由各个轴的方向的偏微分大小综合决定，方向是指向数值增长最快的方向，即函数值增大的方向，如果将梯度方向翻转，很显然会指向函数值减小的方向，而我们要找的就是函数的最低点，我们很显然不可能一步到位，直接到达函数的最低点，所以我们可以随机的赋予w和b参数初值，再利用梯度下降，使其“慢慢的”到达函数最低点，如下图所示（图片引用自网络）：

在上图中我们可以看出，w变化使损失函数慢慢到达最低点，如果我们将梯度下降类比成下山，我们该怎么才能到达山脚。
第一步，明确自己现在所处的位置

第二步，找到相对于该位置而言下降最快的方向

第三步， 沿着第二步找到的方向走一小步，到达一个新的位置，此时的位置肯定比原来低

第四部， 回到第一步

第五步，终止于最低点

按照以上5步，最终达到最低点，这就是梯度下降的完整流程。
了解了流程我们就需要明确，怎么走出下一步，梯度给了我们下一步的方向，下一个w和b的值是什么，也就是下一步的位置在哪？换句话说我们该怎么更新w和b，这里我们引入一个新的参数步长η，也叫学习率，首先我们来看参数更新公式：


即新的w值等于旧值与步长和损失关于w参数的偏导的积的差，b的参数更新公式与w的参数更新公式如出一辙，我们来看一下参数更新公式，通俗的理解就是，我们步长固定，但是在下山的时候如果我们所在的位置山越陡，我们走一步下降的高度差越大，并且我们的方向总沿着梯度下降的方向前进，那是不是步长越大越好呢，很明显不是的，我们来用一张图形象的看一下步长过大会出现什么情况（图片引用自网络）：

我们可以很清楚的看到下一步的落点直接越过了函数的最低点，当越过最低点后重新计算梯度，发现梯度方向与前一个的相反，所以更新参数，但是步长过大，又一次越过函数最低点，这样重复更新会导致震荡，如果运气好震荡多次会达到最低点，如果运气不会则会造成参数持续更新但始终无法到达最低点。（图片引用自网络）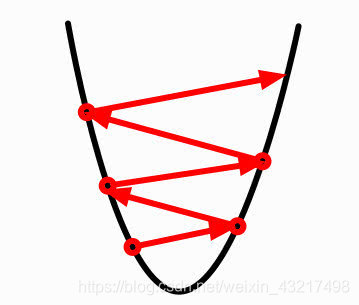
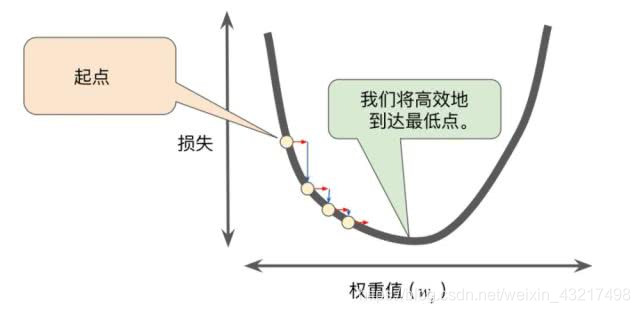
那么如果我们取一个较小的步长会不会更好一些呢?我们直接来看图（图片引用自网络）

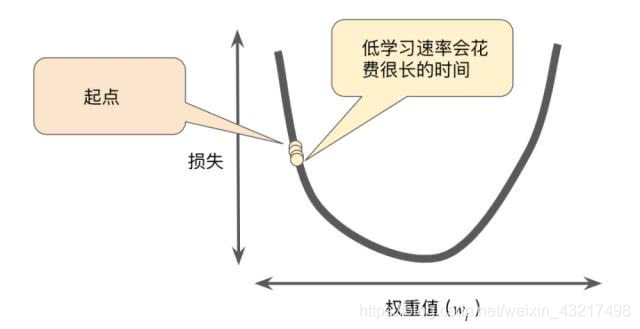
由图我们可以看出，参数会持续更新，但是步长过小，导致需要更新很多次才能达到函数最低点，就像下山的时候走着小碎步，方向是正确的，但是要花费大量的时间，这明显严重的浪费了计算机的计算资源。所以我们需要选择一个合适的步长，使其兼顾效率也不至于造成震荡。（图片引用自网络）

我们目前只说了梯度下降最简单的情况，即只有一个参数更新，我们可以先看看有多个参数时的动态图，以便对于梯度下降有更直观的理解。（图片引用自网络）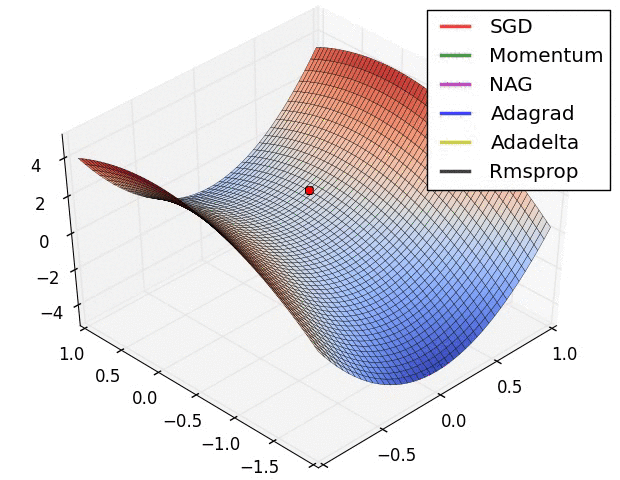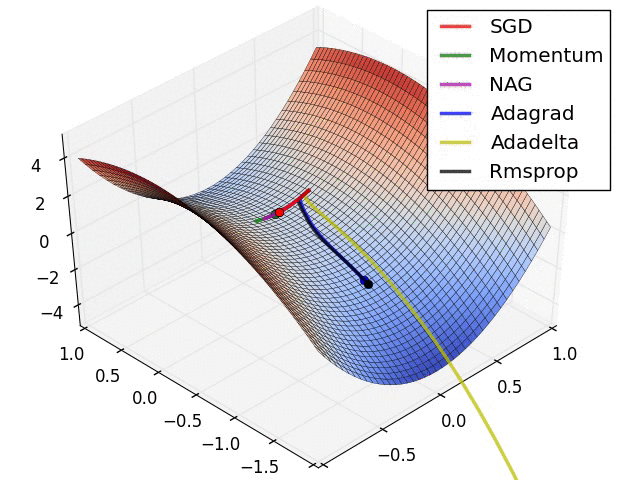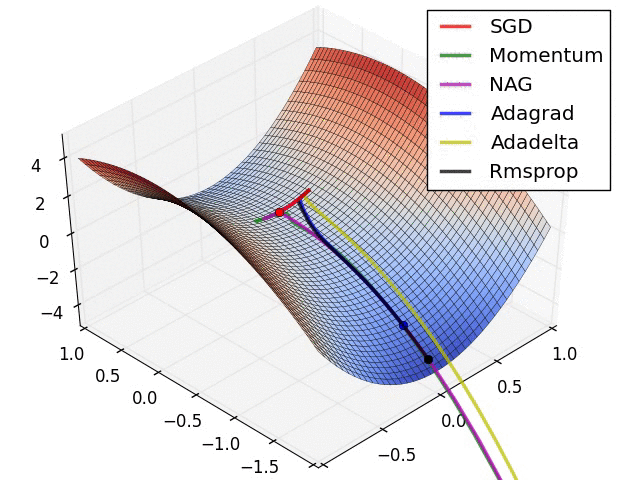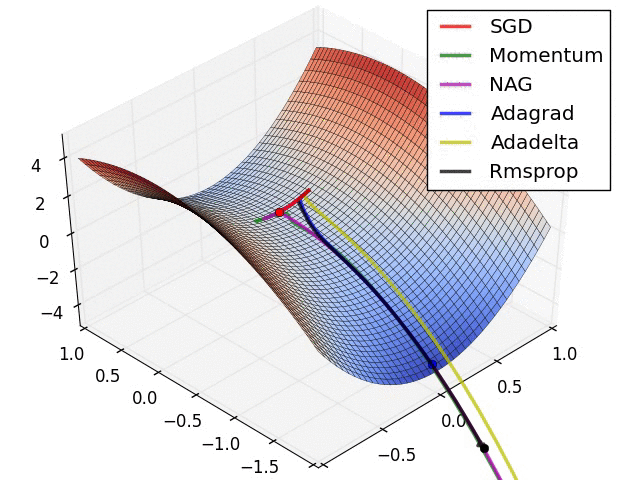
图中不同颜色的线表示不同的优化算法，虽然速度不同，路径不同，但无一例外的都到达了函数的最低点。
OK，到这里我们有了对线性回归的基础理解，我们来解决上文提出来的只有一个因变量的预测问题。

3.使用线性回归解决简单问题

在上文提到的简单数据集中，我们可以看到只有因变量自变量两列数据，所以我们可以使用简单线性回归y = wx + b，根据线性回归求解问题的步骤和公式，我们可以将该程序分成，主函数，梯度计算函数，参数更新函数，损失计算函数四个代码块。

• 损失计算函数

根据损失函数的计算公式我们可以写出如下python代码：

#损失计算函数
def compute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # computer mean-squared-error
        totalError += (y - (w * x + b)) ** 2#所有数据的损失和
    # average loss for each point
    return totalError / float(len(points))

代码的核心就是循环求出所有的数据的平均损失

• 梯度计算和参数更新

因为该例子只有一个自变量一个因变量，我们只需要求损失函数关于w和b的偏导，代码如下：

#梯度计算函数
def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # grad_b = 2(wx+b-y)
        b_gradient += (2/N) * ((w_current * x + b_current) - y)
        # grad_w = 2(wx+b-y)*x
        w_gradient += (2/N) * x * ((w_current * x + b_current) - y)
    # update w'
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]

梯度计算函数的核心为根据偏导公式grad_b = 2(wx+b-y)和grad_w = 2(wx+b-y)*x迭代求解每一个自变量对应的梯度，并且求和。
有了梯度计算有了损失计算，剩下的就是根据损失和梯度更新参数，使其逼进函数最低点。

• 开始训练

根据梯度下降法的解决问题的流程，和规定的迭代次数进行参数计算

def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    # update for several times
    for i in range(num_iterations):#控制迭代次数
        b, w = step_gradient(b, w, np.array(points), learning_rate)
    return [b, w]

• 完整代码

import numpy as np
# y = wx + b
#损失计算函数
def compute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # computer mean-squared-error
        totalError += (y - (w * x + b)) ** 2#所有数据的损失和
    # average loss for each point
    return totalError / float(len(points))
#梯度计算函数
def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        # grad_b = 2(wx+b-y)
        b_gradient += (2/N) * ((w_current * x + b_current) - y)
        # grad_w = 2(wx+b-y)*x
        w_gradient += (2/N) * x * ((w_current * x + b_current) - y)
    # update w'
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]
#更新参数
def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    # update for several times
    for i in range(num_iterations):#控制迭代次数
        b, w = step_gradient(b, w, np.array(points), learning_rate)
    return [b, w]
#开始训练
def run():
	
    points = np.genfromtxt("./data/data.csv", delimiter=",")#delimiter 分割符号
    learning_rate = 0.0001#学习率
    initial_b = 0 # initial y-intercept guess
    initial_w = 0 # initial slope guess
    num_iterations = 1000#迭代次数
    print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
          .format(initial_b, initial_w,
                  compute_error_for_line_given_points(initial_b, initial_w, points))
          )#刚开始的w和b参数 以及初始损失
    print("Running...")
    [b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
    print("After {0} iterations b = {1}, w = {2}, error = {3}".
          format(num_iterations, b, w,
                 compute_error_for_line_given_points(b, w, points))
          )

if __name__ == '__main__':
    run()

运行结果如下

经过线性回归后，我们成功的计算出了w和b参数的值，并且将损失值由五千多降至一百多，由此可见，线性回归可以解决预测问题，Boston房价问题因为参数更多更复杂，我们放在下一节进行讨论。
== 代码所需数据集下载：==链接：https://pan.baidu.com/s/1yc2booiYkC_EzNiBq_pFdw
提取码：f9dv