【学习笔记】线性回归

人们早就知道(并且找到了计算方法)，相比凉爽的天气，在温度较高的时候，蟋蟀鸣叫更为频繁。这里文档给出了我们图片，我们拿一个直尺很容易就能画一条线来近似这种关系。

虽然该直线并没有精确的穿过每个点，但是我们还是能总结出大概的关系:

y = w*x + b

这里的 y 指预测标签(我们预估的值)。

w指x的权重。

b指偏差。

x指特征。

我们可以画出无数条直线来预估这个图片，哪一个效果最好呢？

我们通过loss(这里用的均方误差(MSE))函数，来最大限度的减少损失的模型，这一过程称为经验风险最小化。

损失是一个数值，这个数值表示对单个样本预测的精度，我们训练模型的目标是一组样本中平均损失“较小”的权重和偏差。

我们这里只能找到平均损失较小(传统神经网络存在局部最优解的问题)的权重和偏差，至于原因，在以后会给出。

书中这里给出了MSE的算法， (实际结果-预测结果)的平方和再除以N,

这里N为样本总数。

虽然MSE算法常见于机器学习，但它既不是唯一实用的损失函数，也不是适用于所有情形的最佳损失函数(特殊情况下，我们甚至

需要自己构建损失函数)。

习题答案:

1.均方误差

对于两张图我们可以计算其均方误差。

MSE(左侧) = (0^2 + 1^2 + 0^2 + 1^2 + 0^2 + 1^2 +0^2 + 1^2 + 0^2 + 0^2)/10 = 2/5 = 0.4

MSE(右侧) = (0^2 + 0^2 + 0^2 + 2^2 + 0^2 + 0^2 + 0^2 + 2^2 + 0^2 + 0^2)/10 = 4/5 = 0.8

如果我们直接看残差会发现两者的残差是相等的，就跟之前的《深入浅出的数据分析》中提到的类似，当时书中是用 RMSE来预估模型精度，我们这里是用的MSE。

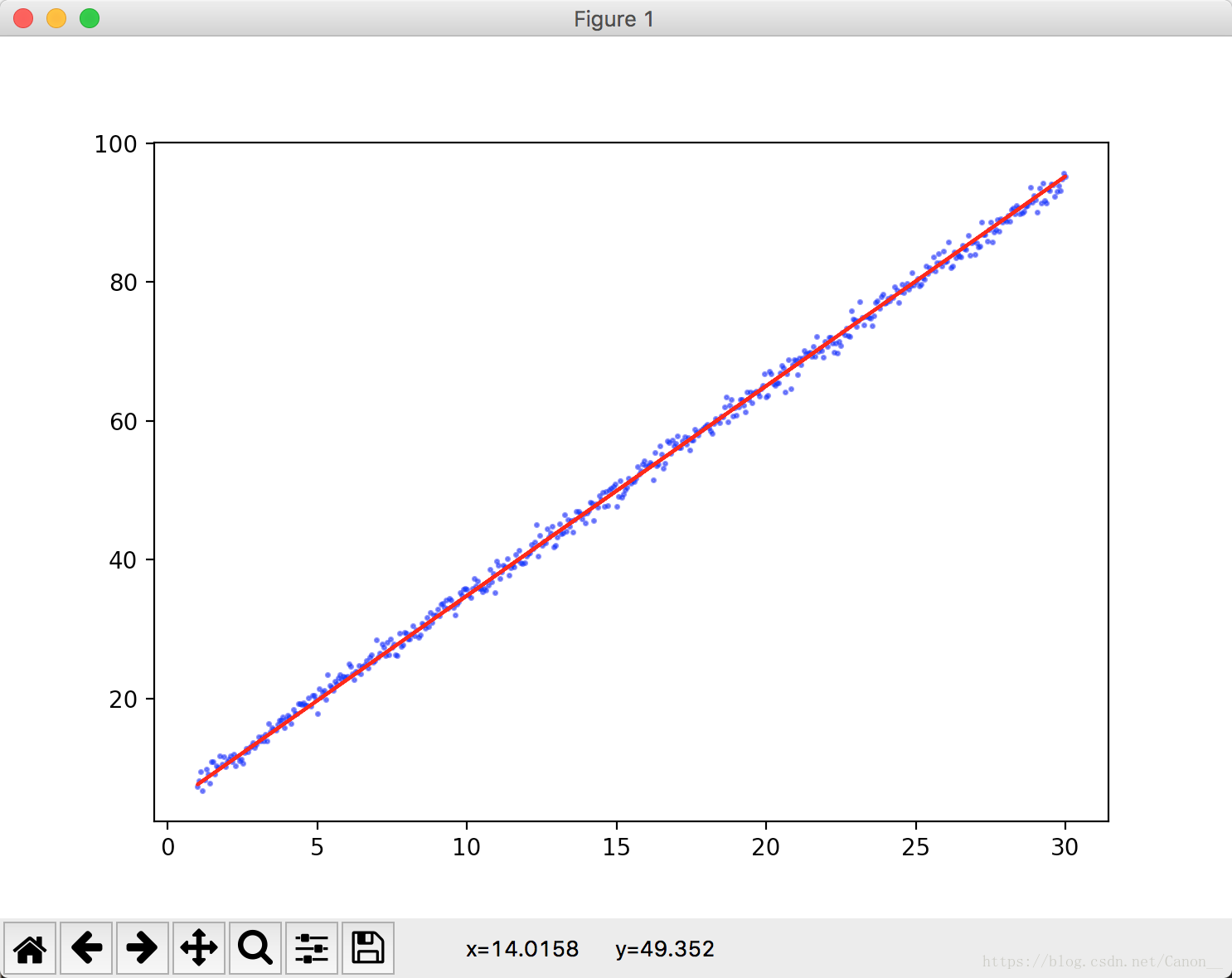
我这里给出一个一元线性回归的例子(基于梯度下降法):

import numpy as np
import tensorflow as tf

x = np.linspace(1, 30, 500)[:, np.newaxis]
np.random.shuffle(x)
y = 3*x + 5 + np.random.standard_normal(500)[:, np.newaxis]

xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])
weights = tf.Variable(tf.random_normal([1]))
biases = tf.Variable(tf.zeros(1) + 0.1)

wx_b = xs * weights + biases

loss = tf.reduce_mean(tf.square(wx_b - ys))

train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

for i in range(5000):
    sess.run(train_step, feed_dict={xs: x, ys: y})
    if i % 50 == 0:
        print(sess.run(loss, feed_dict={xs: x, ys: y}), sess.run(weights), sess.run(biases))

这里的loss我使用的就是MSE,大家在训练神经网络的时候，记得把数据打乱，这样可以让模型学习的更快速。我这里用的np.random.shuffle 来打乱x的顺序，并且给y加入了噪点。最终的运行结果MSE在1.06左右(每个人运行可能有偏差)。

我们可以在这里导入matlab模块来让结果可视化，这里就不写了，感兴趣的可以自己动动手。

【学习笔记】线性回归

猜你喜欢