机器学习入门——详解主成分分析

其他 2020-05-16 10:30:13 阅读次数: 0

引言

本文我们来学习主成分分析法。

主成分分析法(Principal Component Analysis,PCA)是一个非监督的机器学习算法；主要用于数据降维；通过降维，可以发现更利于人类理解的特征；除了降温，还可应用在可视化以及去噪等等。

三万字长文，不建议一次看完

主成分分析

在这里插入图片描述
还是给定一个二维的图像，现在图像上面有两个特征，分别是x轴和y轴。我们先看如何利用PCA对上面的两个特征进行降维，降到一个特征。

在这里插入图片描述
有时我们可以简单的忽略掉不重要的特征。假设这里我们忽略掉特征2，那么所有的点都会落在x轴上，变成如上图所示的图像。

在这里插入图片描述
如果忽略掉特征1，所有的点落在y轴上，变成了上图。

在这里插入图片描述
现在我们有两种降维方式，把它们放到一起，此时哪种方式更好呢。显然右边的更好，因为右边的点更加分散，也就是区分度更好。

那还有没有更好的方式呢？

在这里插入图片描述
我们是否可以作一根直线，让所有的点都映射到这根直线上。

在这里插入图片描述
映射好了之后就变成上面的样子，我们可以把这根直线想成一个轴（一个维度），虽然这根轴是斜的。

使用这种方式，所有的点更加趋近原来点的分布情况，点之间的距离也更加大，区分度更高。现在的问题就成了：如何找到这根让样本间间距最大的轴

那什么是样本间间距呢，如何定义。在概率论与数理统计中有个方差的概念，它是描述样本整体分布疏密的指标，我们就可以使用方差来定义样本间间距，方差 V a r ( x ) Var(x) 公式为：

V a r ( x ) = 1 m ∑ i = 1 m ( x i − x ‾ ) 2 Var(x) = \frac{1}{m}\sum_{i=1}^m (x_i - \overline{x})^2

其中 x ‾ \overline{x} 为样本的均值。

因为我们要找到一个轴，使得样本空间的所有点映射到这个轴后，方差最大。

通常在进行PCA之前，需要对所有样本的均值归零(所有的样本减去样本均值)。

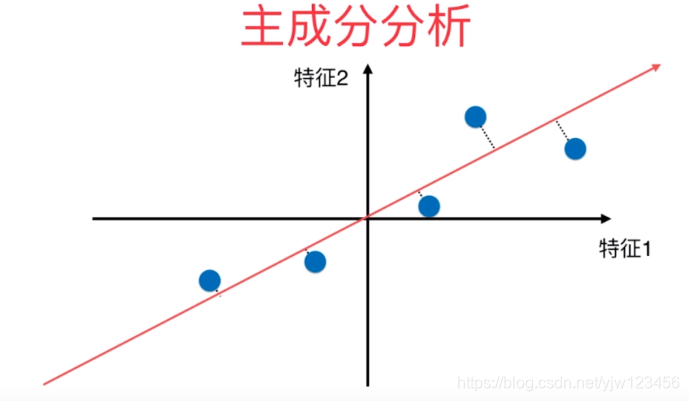
在这里插入图片描述
均值归零后，样本的分布不变，但是坐标轴进行了移动，使得样本在每个维度的均值为零。

现在因为 x ‾ = 0 \overline{x}=0 ，我们可以化简上面计算方差的式子：

V a r ( x ) = 1 m ∑ i = 1 m x i 2 Var(x) = \frac{1}{m}\sum_{i=1}^m x_i^2

这里要注意的是 x i x_i 是映射到新的坐标轴上之后得到的新的样本。

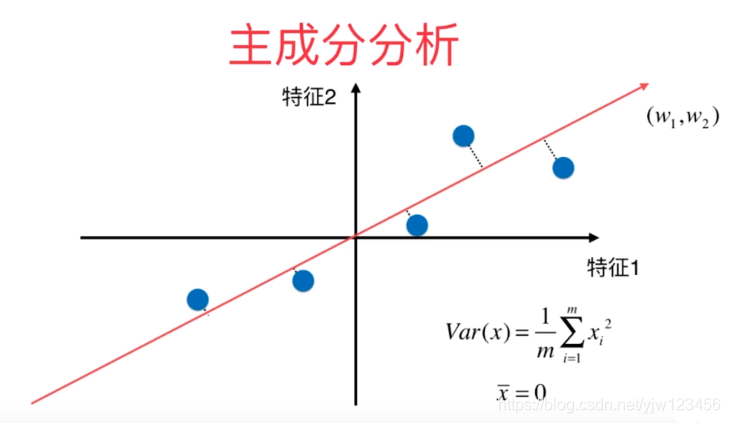
在这里插入图片描述
这个新的轴只有两个维度，我们可以记为 ( w 1 , w 2 ) (w_1,w_2) 。

总结一下，上面说的PCA的过程如下：

在这里插入图片描述
X p r o j e c t X_{project} 是投影到新轴后的样本，我们上面已经知道均值为0，因此可以变成求下面这个式子最大。
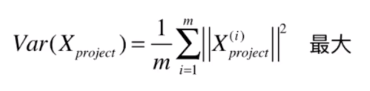
在这里插入图片描述
那我们如何用原来的样本 X i X^i 来表示 X p r o j e c t i X_{project}^i
在这里插入图片描述

这里来看下映射的过程，假设 w = ( w 1 , w 2 ) w=(w_1,w_2) 是我们要找的新轴（这里用一个向量表示），第 i i 个蓝色的样本点 X i X^i 也是一个向量。

将 X i X^i 映射到 w w 上，就是向 w w 表示的轴做一根垂直的直线，垂线与 w w 的交点就是投影(映射)对应的点。

现在我们要求的是 X p r o j e c t i X^i_{project} 的模的平方，其实就是上面这根蓝色的向量对应的平方。

实际上这种映射就是点乘的定义：

X i ⋅ w = ∣ ∣ X i ∣ ∣ ⋅ ∣ ∣ w ∣ ∣ ⋅ c o s θ X^i \cdot w = ||X^i|| \cdot ||w|| \cdot cos\theta

θ \theta 就是上面两个红色向量之间的夹角。

现在我们要找的 w w 是一个轴，也就是一个方向，我们可以用方向向量来表示，也就是说 ∣ ∣ w ∣ ∣ = 1 ||w||=1 。因此上式可以简化为：

X i ⋅ w = ∣ ∣ X i ∣ ∣ ⋅ c o s θ X^i \cdot w = ||X^i|| \cdot cos\theta

∣ ∣ X i ∣ ∣ ||X^i|| 是红色向量的长度，乘以 c o s θ cos\theta 就是投影后的 X p r o j e c t i X_{project}^i 的长度。
所以
X i ⋅ w = ∣ ∣ X p r o j e c t i ∣ ∣ X^i \cdot w = ||X^i_{project}||

因此现在变成了让下面这个最大。
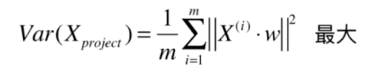
在这里插入图片描述
此时这两个向量点乘后是一个标量，其实可以去掉取模符号。

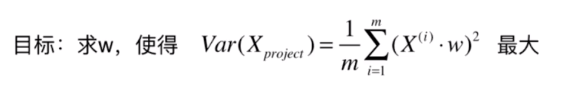
在这里插入图片描述
现在PCA就是要找一个向量 w w ，使得 X X 与 w w 的点乘最大，并且求平均，避免数据规模的影响。
我们这里讨论的只是二维向量，当然可以扩展到多个维度，假设有 n n 个维度，式子就可以展开为：
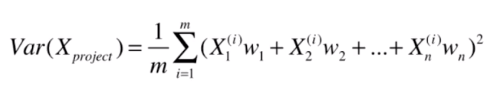
在这里插入图片描述
我们的主成分分析法，就化成了一个目标函数的最优化问题，这里要求最大值，不难想到可以用梯度上升法解决。

这里有必要提到的是，可能大家会觉得PCA和线性回归问题很像。其实差别还是很明显的。

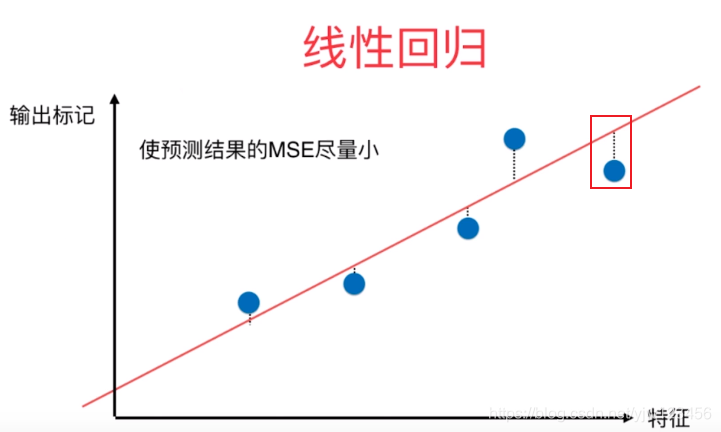
在这里插入图片描述

首先，PCA坐标轴代表的都是特征；而线性回归一般y轴为标签。并且线性回归求的是MSE最小，其实是y轴值相减；而PCA是投影，可以看成是点到直线的垂直距离。

梯度上升法解决主成分分析问题

上小节我们提到过可以使用梯度上升法来解决求目标函数最大值的问题。我们现在就来看下是如何做的。

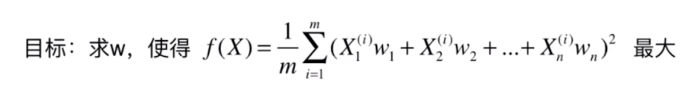
在这里插入图片描述
这里用 f ( X ) f(X) 来表示目标函数。

要使用梯度上升法，我们需要求 f ( X ) f(X) 对 w w 的梯度，这里要注意的是 w w 是未知的，而 X X 是已知的。

f f 对 w w 的每个维度进行求导：
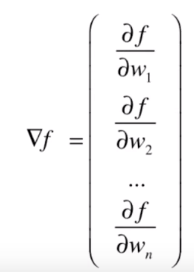
在这里插入图片描述
这个求导很简单，利用链式求导法即可。这里把常数 1 m \frac{1}{m} 提出来：

在这里插入图片描述
我们可以把梯度中括号里面的式子改写成点乘的形式：
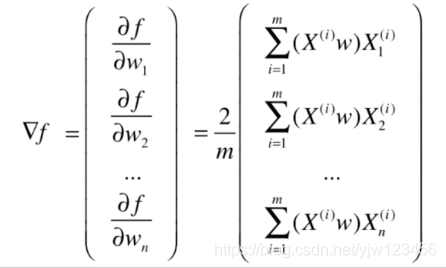
在这里插入图片描述
X X 是 m × n m\times n 的矩阵，而 w w 是 n × 1 n \times 1 的列向量，它们相乘得到 m × 1 m \times 1 的列向量。

此时我们已经可以编程实现的，但是还可以对它们进行向量化处理，避免循环。
我们把 X w Xw 相乘后的结果当成 一个向量，可以写成下面所示，上式就是两个向量与句子点乘的形式。
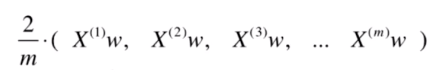
在这里插入图片描述
可以看到下图中每个 X i w X^iw 都是乘以矩阵 X X 中的一列。
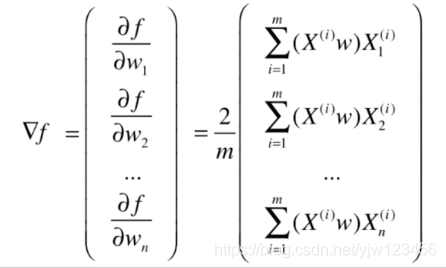
在这里插入图片描述
我们可以写成是 X w Xw 向量与矩阵 X X 相乘，并把后面的矩阵 X X 展开：

在这里插入图片描述
因此可以写成：
在这里插入图片描述
这里 ( X w ) T (Xw)^T 就是行向量( 1 × m 1\times m )，与矩阵 X X 相乘后得到 1 × n 1 \times n 的行向量。

看上图左边的梯度形式(是列向量的形式)，我们也把得到的行向量改成列向量的形式，也很简单，右边整体加个转置即可。

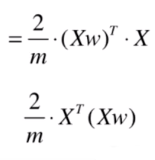
在这里插入图片描述
现在要求 f f 的梯度，只需要计算这样的式子就好了。
在这里插入图片描述

通过向量化的形式，我们可以很容易的编程实现。下面我们就来编程实现一下。

编程实现PCA

还是先用模拟数据来实现

import numpy as np
import matplotlib.pyplot as plt
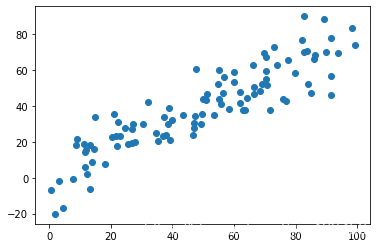
X = np.empty((100,2))#100个二维样本
X[:,0] = np.random.uniform(0.,100.,size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0.,10.,size=100)
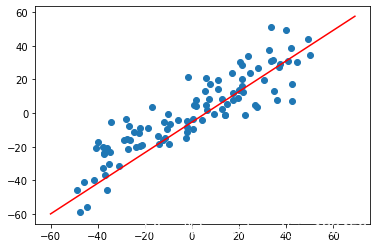
plt.scatter(X[:,0],X[:,1])
plt.show()

在这里插入图片描述
下面用上小节讲的方式对这个数据进行降维。首先编写均值归零函数：

def demean(X):
    # X是一个矩阵，每一行代表一个样本
    return X - np.mean(X,axis=0) #求的是每一列(每个维度)的均值

我们来测试一下这个函数：

X_demean = demean(X)
plt.scatter(X_demean[:,0],X_demean[:,1])
plt.show()

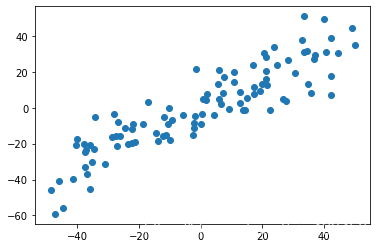
在这里插入图片描述
可以看到，数据分布还是一致的，只不过(0,0)到了上图中心点位置。我们可以验证下每个维度的均值是否为零：

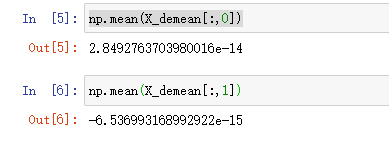
在这里插入图片描述
这里都输出了两个很小的数字，基本可以认为是零了。

下面使用梯度上升法来求解PCA。

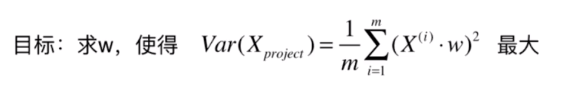
在这里插入图片描述

# 目标函数
def f(w,X):
    return np.sum((X.dot(w)**2)) / len(X)

首先编写目标函数的代码。

在这里插入图片描述

# 目标函数的梯度
def df_gradient(w,X):
    return X.T.dot(X.dot(w)) * 2. / len(X)

再是目标函数的梯度。

下面就可以实现梯度上升法了。

def gradient_ascent(df,X,initial_w,eta,n_iters=1e4,epsilon=1e-8):
    cur_iter = 0
    while cur_iter < n_iters: #迭代次数耗完跳出
        gradient = df(w,X)
        last_w = w
        w = w + eta * gradient #梯度上升法这里取加号
        if abs(f(w,X) - f(last_w,X)) < epsilon: #如果增加的值没有超过阈值，则跳出
            break
        cur_iter += 1
    return w

整个算法和我们上篇介绍的梯度下降法非常像，除了计算w = w + eta * gradient时的符号号不同。

上面我们推导式子的时候，说过 w w 定成单位方向向量，也就是模为 1 1 ，因此这里还需要进行一下处理。

def direction(w):
    return w / np.linalg.norm(w) # np.linalg.norm是求模操作，让w除以它的模就可以了

因此，我们改写下梯度上升的算法就可以了：

def gradient_ascent(df,X,initial_w,eta,n_iters=1e4,epsilon=1e-8):
    w = direction(initial_w) #转换成单位向量
    cur_iter = 0
    while cur_iter < n_iters: #迭代次数耗完跳出
        gradient = df(w,X)
        last_w = w
        w = w + eta * gradient #梯度上升法这里取加号
        w = direction(w)
        if abs(f(w,X) - f(last_w,X)) < epsilon: #如果增加的值没有超过阈值，则跳出
            break
        cur_iter += 1
    return w

下面我们调用下这个梯度上升法。

# 初始化w为随机数，不能初始化为0
initial_w = np.random.random(X.shape[1])
eta = 0.001
# PCA过程中不能使用StandardScaler标准化数据,不让我们数据的标准差都为1
gradient_ascent(df_gradient,X_demean,initial_w,eta)

在这里插入图片描述
这里已经得到了 w w 了，然后我们绘制下方向为 w w 的轴。

# 初始化w为随机数，不能初始化为0
initial_w = np.random.random(X.shape[1])
eta = 0.001
# PCA过程中不能使用StandardScaler标准化数据,不让我们数据的标准差都为1
w = gradient_ascent(df_gradient,X_demean,initial_w,eta)
plt.scatter(X_demean[:,0],X_demean[:,1])

plt.plot([-60,w[0]*90],[-60,w[1]*90],color='r') #绘制w方向的直线，以(-60,w[0]),(-60,w[1])为方向，将整段线的长度乘以90，使看起来长一些
plt.show()

在这里插入图片描述
这个红线对应的轴就是我们说的一个主成分，它是我们求出来的第一个主成分，所以我们叫它为第一主成分。

我们这里求解的是二维数据的一个主成分，对二维数据来说映射到一维就够了，但如果是1000维的数据，显然不能映射到一维上。我们可能需要映射到10维上或100维上。

因此，只是求出第一个主成分是不够的，我们还要求出第二主成分、第三主成分…

下面就介绍如何求前n个主成分。

求数据的前n个主成分

在这里插入图片描述

上面我们将这个二维数据映射到了红线这条轴上，这个轴就是我们的第一主成分，得到的结果是样本点在这个轴上方差是最大的。

但是我们的样本点本身是二维点，把它映射到这个新轴上也是二维数据，它应该还有另外一个轴。这是对二维数据来说，对n维数据，通过主成分分析法重新进行排列，使得第一个轴保持样本方差是最大的，第二个轴样本方差次之，第三个轴再次之。

主成分分析法本质是从一组坐标系转移到另外一组坐标系。现在我们求出了第一个轴所在的方向，我们如何求出下一个轴所在的方向呢，也就是求出下一个主成分。

只要改变数据，将数据在第一个主成分上的分量去掉。
在这里插入图片描述
上面我们说过，在第一主成分方向上的投影是这样的。并且有 X ⋅ w = ∣ ∣ X p r o j e c t i ∣ ∣ X \cdot w = ||X^i_{project}|| 。

如果让投影向量的模再乘上 w w 这个单位方向方向，最终结果就是 X p r o j e c t i X^i_{project} 这个向量。

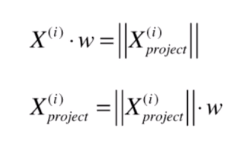
在这里插入图片描述
那如何去掉 X i X^i 这个样本在 X p r o j e c t i X^i_{project} 向量上的分量呢？

在这里插入图片描述
只要减去 X p r o j e c t i X^i_{project} 即可，几何意义是将 X i X^i 这个样本映射到与向量 X p r o j e c t i X^i_{project} 相垂直的向量上(绿色向量)。

这样就得到了 X ′ i X^{\prime i} ，是 X i X^i 中去掉了第一主成分分量的结果。

现在想要求第二主成分，只要在新的数据 X ′ i X^{\prime i} 上求第一主成分即可，以此类推，可以求前n主成分。

下面编程实现，我们先修改下上一节的代码，改成如下：

import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100,2))#100个二维样本
X[:,0] = np.random.uniform(0.,100.,size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0.,10.,size=100)

def demean(X):
    # X是一个矩阵，每一行代表一个样本
    return X - np.mean(X,axis=0) #求的是每一列(每个维度)的均值

# 目标函数
def f(w,X):
    return np.sum((X.dot(w)**2)) / len(X)

# 目标函数的梯度
def df_gradient(w,X):
    return X.T.dot(X.dot(w)) * 2. / len(X)

def direction(w):
    return w / np.linalg.norm(w) # np.linalg.norm是求模操作，让w除以它的模就可以了

# 改成第一主成分，直接调用df_gradient
def first_component(X,initial_w,eta,n_iters=1e4,epsilon=1e-8):
    w = direction(initial_w) #转换成单位向量
    cur_iter = 0
    while cur_iter < n_iters: #迭代次数耗完跳出
        gradient = df_gradient(w,X)
        last_w = w
        w = w + eta * gradient #梯度上升法这里取加号
        w = direction(w)
        if abs(f(w,X) - f(last_w,X)) < epsilon: #如果增加的值没有超过阈值，则跳出
            break
        cur_iter += 1
    return w

接下来先求第一主成分

# 初始化w为随机数，不能初始化为0
initial_w = np.random.random(X.shape[1])
eta = 0.001

w = first_component(X_demean,initial_w,eta)
w # array([0.76863446, 0.63968826])

然后根据去掉第一主成分分量：

X2 = np.empty(X.shape)
for i in range(len(X)):
    X2[i] = X[i] - X[i].dot(w) * w 
    
plt.scatter(X2[:,0],X2[:,1])
plt.show()

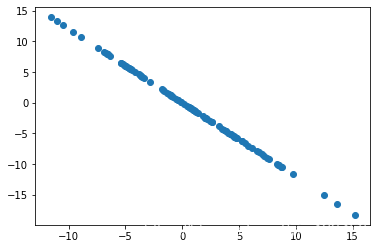
在这里插入图片描述
并绘制出它的图形，是一条从左上角到右下角的直线。
在这里插入图片描述

我们第一主成分的向量是上图红线所示，现在所有的样本数据去掉这个方向的分量，得到的结果就是和这个向量方向垂直的那个方向对应的分量，就是那条从左上角到右下角的直线。

在这里插入图片描述
因为我们只有两个维度，去掉第一主成分后，剩下的第二个维度就是所有的内容了。所以样本在第二个维度上的分布就完全在这一根直线了，完全没有其他方向的方差。

此时我们可以尝试下求第二主成分对应的轴是怎样的。

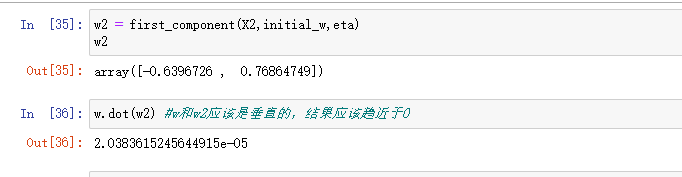
w2 = first_component(X2,initial_w,eta)
w2

w2其实就是上面这根直线的方向。
在这里插入图片描述

上面我们通过

X2 = np.empty(X.shape)
for i in range(len(X)):
    X2[i] = X[i] - X[i].dot(w) * w

这段代码求X2的时候用了for循环，其实是可以向量化的。

X2 = X - X.dot(w).reshape(-1,1) * w # mxn * nx1 -> mx1 * 1xn -> mxn    => mxn - mnx

这里我们分别求出了第一主成分和第二主成分，如果要求第三主成分还要再次写重复代码。因此这里将这些代码合并一下：

# 求出X的前n个主成分
def first_n_component(n,X,eta=0.01,n_iters=1e4,epsilon=1e-8):
    X_copy = X.copy()
    X_copy = demean(X_copy)
    res = []#保存前n个主成分
    for i in range(n):
        initial_w = np.random.random(X_copy.shape[1])#初始化非零w
        w = first_component(X_copy,initial_w,eta) #调用上面的函数
        res.append(w)
        X_copy = X_copy - X_copy.dot(w).reshape(-1,1) * w # 去掉刚求出来的主成分分量
    return res

下面可以直接求前两个主成分

res = first_n_component(2,X)

并且验证是否垂直
在这里插入图片描述
我们这小节使用的是二维数据，下面使用高维数据来演示一下。并且主成分分析法主要作用是降维，我们到现在为止只不过是转换坐标系而已。那如何将高维样本数据映射到低维空间呢？一且看下一小节分析。

高维数据映射为低维数据

如何利用PCA对数据进行降维呢？

在这里插入图片描述
(上图右边矩阵最后一行应该都是 W i ( k ) W^{(k)}_i )

假设我们的原数据 X X 有 m m 行 n n 列，就是有 m m 个样本， n n 个特征。
通过我上面介绍的主成分分析法，假设我们已经求出针对这个数据集 X X 的前 k k 个主成分 W k W_k 。

它有 k k 行，代表前 k k 个主成分；对于每一行，有 n n 个元素，代表主成分的坐标轴有 n n 个维度的。因为是从一个坐标系转换到另一个坐标系，坐标系的维度是不变的。

那我们如何将我们的样本 X X 从 n n 维转换为 k k 维呢？
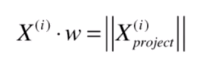
在这里插入图片描述

回顾下上面我们学过的内容，我们将一个样本 X 1 X^1 与 W 1 W^1 进行点乘，点乘后的结果就是讲这个样本映射到 w w 这个轴上得到的模（大小）。

如果我们将这个样本与 k k 个 w w 分别做点乘的话，那么得到的结果就是这个样本在这 k k 个方向上，每个方向相应的大小。

这 k k 个元素合在一起，就能表示该样本映射到 k k 个轴所代表的坐标系上相应的样本大小。

因为我们让样本 X 1 X^1 去点乘 W 1 , W 2 , ⋯   , W k W_1,W_2,\cdots,W_k ，我们就可以得到 k k 个数(模，标量)，这 k k 个数组成的向量，就是样本 X 1 X^1 映射到 W k W_k 这个坐标系上得到的 k k 维向量。

由于 k < n k < n ，我们就完成了一个样本从 n n 维项 k k 维度的映射(降维)。

依此类推，我们对所有的样本都进行这样的操作，就能将所有的样本从 n n 维映射到 k k 维。

因此实际上就是一个矩阵的乘法 X ⋅ W k T X \cdot W_k^T

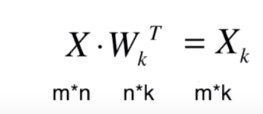
在这里插入图片描述

X X 是 m × n m\times n 的； W k W_k 是 k × n k\times n 的, W k T W_k^T 就是 n × k n \times k 的。因此它们相乘的结果就是 m × k m\times k 的。这样，就把这 m m 个样本的维度从 n n 维降到了 k k 维。

降维后的样本我们记为 X k X_k 。
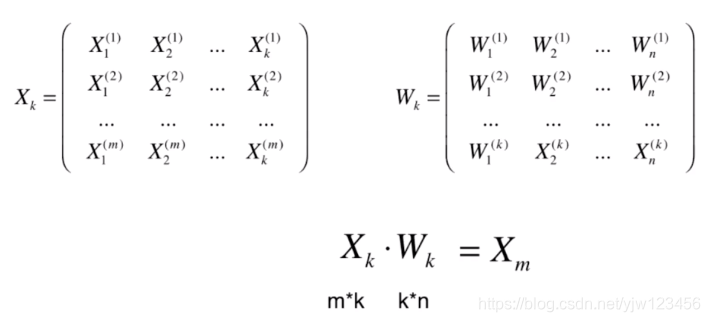
在这里插入图片描述

我们求得了 X k X_k 后，还可以通过 W k W_k 来将 X k X_k 恢复为原来的 n n 维数据。
恢复的过程也很简单，现在 X k X_k 每行有 k k 个元素，让它乘以 W k W_k 的每一列。

相当于把 X k X_k 的每一行映射到 W k W_k 中每一列对应的方向中，而 W k W_k 有 n n 列的，最终就恢复成了 m × n m \times n 的矩阵 X m X_m 。

但是恢复后的结果已经不是原来的了。因为在降维的过程中会丢失一些信息，这些丢失的信息是恢复不过来的。但是这个反向的操作从数学的角度来看是成立的。

下面来编程实现下，并且封装到一个类中：

import numpy as np


class PCA:
    def __init__(self, n_components):
        '''

        :param n_components: n个主成分
        '''
        self.n_components = n_components
        self.components_ = None  # 保存这n个主成分

    def fit(self, X, eta=0.01, n_iters=1e4):
        '''获得数据集X的前n个主成分'''

        def demean(X):
            # X是一个矩阵，每一行代表一个样本
            return X - np.mean(X, axis=0)  # 求的是每一列(每个维度)的均值

        # 目标函数
        def f(w, X):
            return np.sum((X.dot(w) ** 2)) / len(X)

        # 目标函数的梯度
        def df_gradient(w, X):
            return X.T.dot(X.dot(w)) * 2. / len(X)

        def direction(w):
            return w / np.linalg.norm(w)  # np.linalg.norm是求模操作，让w除以它的模就可以了

        def first_component(X, initial_w, eta, n_iters=1e4, epsilon=1e-8):
            w = direction(initial_w)  # 转换成单位向量
            cur_iter = 0
            while cur_iter < n_iters:  # 迭代次数耗完跳出
                gradient = df_gradient(w, X)
                last_w = w
                w = w + eta * gradient  # 梯度上升法这里取加号
                w = direction(w)
                if abs(f(w, X) - f(last_w, X)) < epsilon:  # 如果增加的值没有超过阈值，则跳出
                    break
                cur_iter += 1
            return w

        X_pca = demean(X)
        # n_components行 X.shape[1](X样本对应的列数)列
        self.components_ = np.empty(shape=(self.n_components, X.shape[1]))

        for i in range(self.n_components):
            initial_w = np.random.random(X_pca.shape[1])  # 初始化非零w
            w = first_component(X_pca, initial_w, eta)  # 调用上面的函数
            self.components_[i, :] = w  # 放到第i行位置
            X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w  # 去掉刚求出来的主成分分量

        return self

    def transform(self, X):
        '''将给定的X，映射到各个主成分分量中'''
        return X.dot(self.components_.T)  # X⋅W^T_k

    def inverse_transform(self, X):
        '''将低维数据映射回高维数据'''
        return X.dot(self.components_)

    def __repr__(self):
        return "PCA(n_components=%d)" % self.n_components

然后我们还是拿这份数据来测试一下：

在这里插入图片描述

pca = PCA(n_components=1)
pca.fit(X)
X_reduction = pca.transform(X)
X_reduction.shape

这里我们尝试将这个二维数据降维到一维。
在这里插入图片描述

我们再尝试恢复成二维：

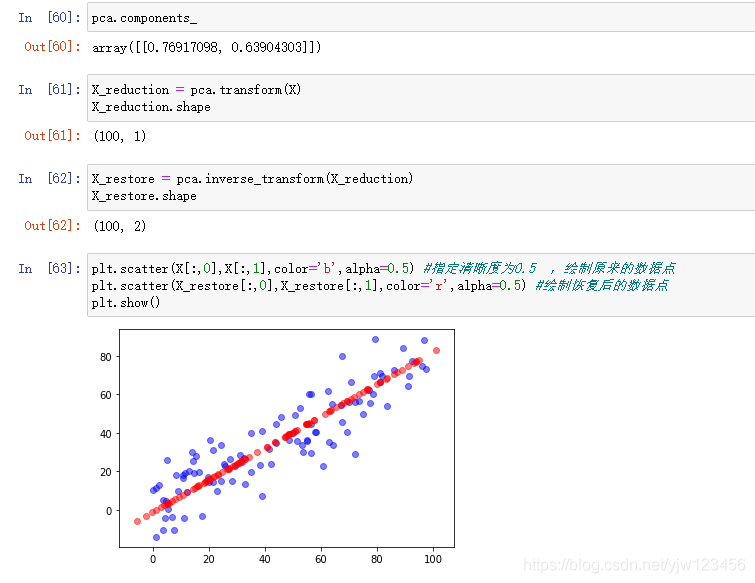
plt.scatter(X[:,0],X[:,1],color='b',alpha=0.5) #指定清晰度为0.5  ，绘制原来的数据点
plt.scatter(X_restore[:,0],X_restore[:,1],color='r',alpha=0.5) #绘制恢复后的数据点
plt.show()

在这里插入图片描述

可以看到，我们的数据经过降维再恢复之后，就成了所有数据点在主成分的这个轴上的位置。此时所有的红点都在一条直线上，但是是由二维特征所表示的。

到此PCA原理与实现就介绍完了，下面我们看下sklearn中的PCA。

sklearn中的PCA

from sklearn.decomposition import PCA
pca = PCA(n_components=1)
pca.fit(X)

在这里插入图片描述

可以看到sklearn求出的第一主成分和我们求得的相差不多。

在这里插入图片描述
我们进行同样的操作，可以看到和我们自己代码实现的结果差不多。

上面我们使用的数据集是随机生成的，没什么意思。下面我们看下真实的数据集。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split

# 手写数字识别
digits = datasets.load_digits()
X = digits.data
y = digits.target

X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=777)
X_train.shape # (1347, 64)

数据准备完毕，下面我们用knn算法来看下准确率是多少，并且记录耗时。

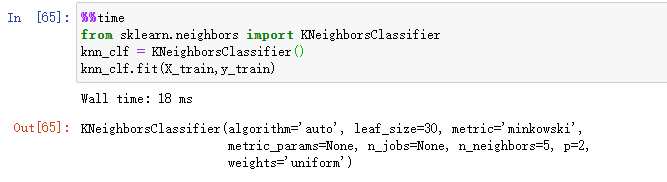
%%time
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train,y_train)

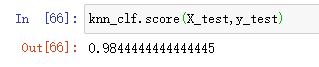
在这里插入图片描述
然后看下识别准确率：
在这里插入图片描述
下面我们尝试用PCA对这些数据进行降维。

from sklearn.decomposition import PCA
pca = PCA(n_components=2) #先降到二维
pca.fit(X_train)
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test) #使用同样的pca对象来转换X_test，不能通过X_test数据集重新训练一个pca

这里直接降到二维，之前是64维的数据，然后用降维后的数据来训练一个新的knn模型。

在这里插入图片描述
可以看到将高维数据降到低维后可以减少计算时间，这里识别准确率降低到了57%。

这里产生了一个矛盾，我们将64维的信息降到2维以后，虽然训练速度变快了，但是识别准确率降低的太夸张了。 显然2维太低了，我们可以尝试10维、20维的数据。
但是我们具体应该降到多少维呢，除了使用参数搜索的方式一个一个尝试外，还可以使用sklearn中PCA给我们提供的指标来控制我们保持的准确率。

这个指标是pca.explained_variance_ratio_，意思是可解释的比例。

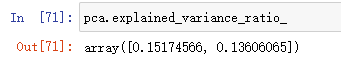
在这里插入图片描述
可以看到第一个轴它能解释15%原数据的方差；第二个轴它能解释%13.6原数据的方差。

我们PCA的过程就是寻找主成分，使得原来的数据相应的方差维持的最大，上面这个值就告诉我们维持了原来数据所有方差的百分之多少。

对于我们这两个维度来说，它涵盖了原来数据总方差的15%+13.6%=28.6%。剩下的71.4%的方差信息就丢失了。显然丢失的信息过多。

我们可以通过这个变量来找到应该降到多少维。

pca = PCA(n_components=X_train.shape[1]) #先传入原数据的所有维度数
pca.fit(X_train)
pca.explained_variance_ratio_

在这里插入图片描述
然后我们可以看到64个数值，这64个数值是从大到小倒序排列的。它的意思是对于每个主成分来说，依次可以解释的方差是多少。

可以理解为每个方向轴对应的重要程度。我们可以做一个折线图。

plt.plot([i for i in range(X_train.shape[1])],[np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()

在这里插入图片描述
就是随着方向轴数的增加，能表示的方差信息，最高是1。可以看到当取35左右的时候是比较合适的，后面再增加的话也增长不了多少。

当然还可以指定希望我们的数据保持多少的信息，比如指定为95%，就可以得到对应的横轴坐标值是多少。

这个功能被sklearn封装好了，可以直接传入到构造函数中。

pca = PCA(0.95) #希望降维后的数据能解释95%的方差
pca.fit(X_train)

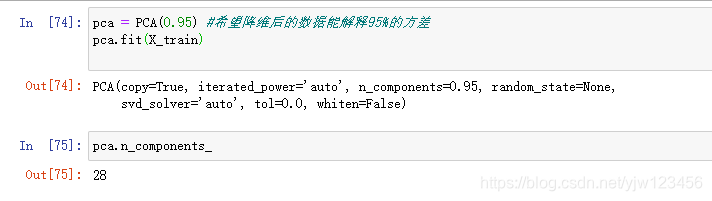
在这里插入图片描述
可以看到，使用28维的数据就能解释我们原数据95%以上的方差，也就是说，我们只丢失了5%的信息。

此时就可以计算出这种情况下的准确率是多少了，当然先要按照这个pca对数据进行降维。

X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test) #使用同样的pca对象来转换X_test，不能通过X_test数据集重新训练一个pca

并打印新的knn模型训练耗时

%%time
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction,y_train)

在这里插入图片描述
之前原数据是18ms，耗时的减少也是很可观的。那准确率又是多少呢？

在这里插入图片描述
可以看到准确率少了0.07左右，但是时间却大大缩小的。有时我们愿意用准确率来换时间。

还有上面我们把数据降到2维，其实并不是完全没有意义的，可以很容易想到的是，我们可以对2维数据进行可视化。

pac =PCA(n_components=2)
pca.fit(X)
X_reduction = pca.transform(X) #降到2维
for i in range(10):#绘制数字0到9
    plt.scatter(X_reduction[y==i,0],X_reduction[y==i,1],alpha=0.8)
plt.show()

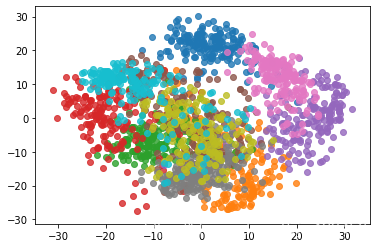
在这里插入图片描述
绘制的结果如上图所示，虽然我们没有指定颜色，但是matplotlib会自动为我们分配颜色。

这里还可以加上标签，看下到底是哪些数字：

pac =PCA(n_components=2)
pca.fit(X)
X_reduction = pca.transform(X) #降到2维
for i in range(10):#绘制数字0到9
    plt.scatter(X_reduction[y==i,0],X_reduction[y==i,1],alpha=0.8,label=i)
plt.legend()
plt.show()

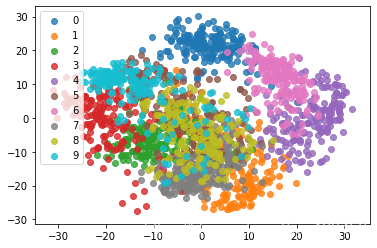
在这里插入图片描述
可以看到这个二维空间中很多数字之间的区分度还是很明显的。比如蓝色的数字0和紫色的数字6以及红色的数字3之间区分是较大的。

我们甚至可以分析这个图像，来得到一些结论。如果我们只想区分数字0和数字3，那么很有可能使用二维的数据就足够了。

试试MNIST数据集

sklearn中的手写数字集维度比较小，并且样本数不多。我们该小节来试下MNIST手写数据集。

# 加载MNIST数据集
import numpy as np
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784',version=1) #这可能会耗费一些时间
X,y = mnist['data'],mnist['target']
X.shape

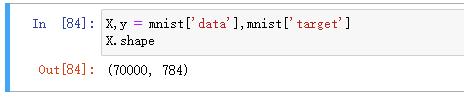
在这里插入图片描述
可以看到MNIST有70000个数据，每个数据有784维(28*28)。
通常我们用前60000个数据作为训练集，后10000个数据作为验证集。

X_train = np.array(X[:60000],dtype=float)
y_train = np.array(y[:60000],dtype=float)
X_test = np.array(X[60000:],dtype=float)
y_test = np.array(y[60000:],dtype=float)

下面我们使用knn来进行识别。

from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier()
%time knn_clf.fit(X_train,y_train)#对60000个样本进行训练

在这里插入图片描述
足足等了半分钟，是不是觉得挺慢的，还是太年轻，计算准确率更慢，虽然sklearn已经通过kd树进行优化过了。

%time knn_clf.score(X_test,y_test)

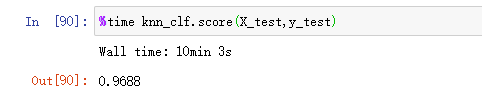
在这里插入图片描述

耗时10分钟。从这里可以看出来，当数据样本非常多、维度非常大时，机器学习算法是非常耗时的。这也是为什么要使用PCA这种降维方法来对样本进行降维了。

这里我们虽然没用使用StandardScaler对数据进行归一化，但是手写数字样本本身是在同一个尺度下的，两个样本直接进行比较是有意义的。
当数据的尺度不同的时候，我们才要使用StandardScaler，将它们放到同样的尺度上。

下面我们使用PCA进行降维，来看下训练结果与耗时。

from sklearn.decomposition import PCA
pca = PCA(0.9) #由于样本量较大，我们只保留90%的信息
pca.fit(X_train)
X_train_reduction = pca.transform(X_train) #降维
X_train_reduction.shape #看下降到多少维了

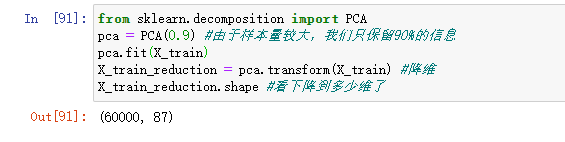
在这里插入图片描述

可以看到降到了87维，然后用降维后的数据来训练knn分类器。

knn_clf = KNeighborsClassifier()
%time knn_clf.fit(X_train_reduction,y_train)#使用降维后的数据训练knn分类器

在这里插入图片描述
只要1.51秒，那么计算准确率是多少呢

X_test_redunction = pca.transform(X_test)#对X_test降维
%time knn_clf.score(X_test_redunction,y_test)

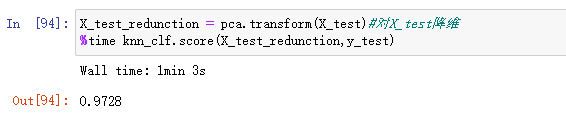
在这里插入图片描述

可以看到我们只用了1分钟就完成了计算准确率，并且准确率有97.28%，比之前的10分钟快了10倍。

如果仔细看的话，会发现降维后，准确率反而提高了。就是说，我们不仅把数据变小了，相应的训练过程和预测过程耗时也变小的，重要的是准确率还提高了。

这是因为PCA还可以进行降噪！

在降维的过程中很有可能将原有数据包含的噪音给消除了，使得我们可以更加准确的拿到数据集对应的特征，从而使得识别准确率得到提升。

下面我们举一个例子来说明PCA降噪的应用。

使用PCA降噪

在这里插入图片描述

首先回顾下我们造的二维数据，我们在二维数据中加入了噪音。造成了这个数据集在一根斜线上下进行抖动。

假如某个数据集展现出来了这种结果，是不是可能数据集本身的分布就是一根直线呢？也就是这个数据集在某条直线上下的抖动实际上是一种噪音。

噪音的产生原因有很多：测量仪器的误差、计量人员的粗心、实际测量手段有问题等。

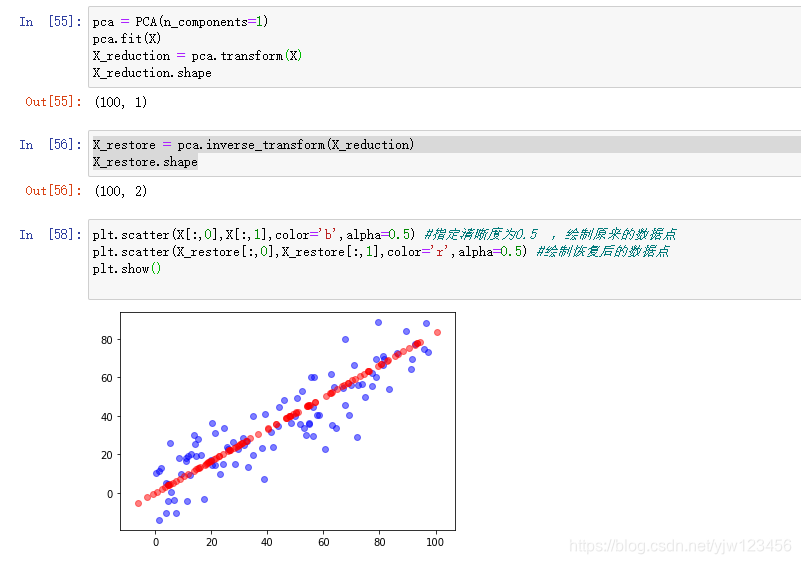
在这里插入图片描述
我们上面将 X X 降维成1维数据，再将它恢复成了二维数据(上面红色样本点)。此时的红色数据是一条直线，我们比较下红色样本和蓝色样本。
我们可以把这个过程理解为去掉蓝色样本的噪音。

当然在实际情况下，我们无法确定红色样本数据一点噪音都没有，也无法确定所有的蓝色样本点上下抖动都是因为噪音引起的。

但是从蓝色样本数据到红色样本数据我们丢失了信息，我们丢失的信息很有可能大部分都是噪音。

为了更加直观的说明降噪这一点，我们再次使用sklearn的手写数字数据集。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split

# 手写数字识别
digits = datasets.load_digits()
X = digits.data
y = digits.target

# 制造有噪音的数据
noisy_digits = X + np.random.normal(0,4,size=X.shape)  #均值为0方差为4的噪音

先是制造噪音数据。

example_digits = noisy_digits[y==0,:][:10] #取10个标签为0的样本
for num in range(1,10): #从数字1到9中分别取出前10个
    X_num = noisy_digits[y==num,:][:10]
    example_digits = np.vstack([example_digits,X_num]) #将example_digits和X_num放在一起
example_digits.shape

在这里插入图片描述

example_digits = noisy_digits[y==0,:][:10] #取10个标签为0的样本
for num in range(1,10): #从数字1到9中分别取出前10个
    X_num = noisy_digits[y==num,:][:10]
    example_digits = np.vstack([example_digits,X_num]) #将example_digits和X_num放在一起
example_digits.shape

然后我们每个标签中取前10个样本，得到100个样本的数据，最后我们绘制在一张图中。

def plot_digits(data):
    fig,axes = plt.subplots(10,10,figsize=(10,10),subplot_kw={'xticks':[],'yticks':[]},
                           gridspec_kw=dict(hspace=0.1,wspace=0.1))
    for i,ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8,8),cmap='binary',interpolation='nearest',clim=(0,16))
    plt.show()
    
plot_digits(example_digits)

在这里插入图片描述
因为增加了噪音，大概可以看到第0行都是数字0；第1行都是数字1…

下面我们使用PCA的方式进行降噪。

pca = PCA(0.5) #因为噪音看起来比较大，所以我们只保存50%的信息
pca.fit(noisy_digits)
# 下面进行降维
components = pca.transform(example_digits)
#再恢复为64维
filtered_digits = pca.inverse_transform(components) 
plot_digits(filtered_digits)

在这里插入图片描述
可以看到，降维到了12维，我们继续绘制出恢复后的样本。
在这里插入图片描述
虽然还是有点模糊，但是相比降噪之前的样子，好了很多。

这就是我们使用PCA的方式进行降噪的DEMO。

PCA除了可以降维、降噪还可以用在人脸识别中，我们一起来看下吧。

人脸识别与特征脸

PCA在人脸识别中的应用是特征脸。这是啥意思呢
在这里插入图片描述
我们之前说过，对于样本 X X 从 n n 维空间，映射到 k k 维空间，我们只要使用PCA算法，求出它的前 k k 个主成分就好了。

每个样本都与 W k W_k 的矩阵做点乘得到的结果就是每个样本在 W k W_k 中每行所表示的轴上的映射向量的大小。

这里我们可以换种思路来想，对于 W k W_k 这个矩阵来说，它也有 n n 列，如果将 W k W_k 中的每行都想成一个样本的话，那代表什么呢？

对于 W k W_k 来说，每行都代表一个方向，第一行是最重要的方向，第二行是次重要的方向。
看成样本的话，可以说第一行的样本是最重要的样本，最能反映原来 X X 矩阵的样本，第二行所代表的样本是次重要的样本。

在人脸识别中， X X 中每行代表每张人脸图像，而 W k W_k 中的每行也可以理解为一个人脸图像， W k W_k 中的人脸图像就叫特征脸。

下面我们编程来看下这些特征脸是什么样子的。

from sklearn.datasets import fetch_lfw_people #人脸识别数据库

faces = fetch_lfw_people() #第一次加载需要时间

(博主第一次加载人脸识别数据就失败了，建议从别处直接下载这个数据集，可以参考这篇文章)

在这里插入图片描述

下面随机绘制36张脸。

def plot_faces(faces):
    fig,axes = plt.subplots(6,6,figsize=(10,10),subplot_kw={'xticks':[],'yticks':[]},
                           gridspec_kw=dict(Hspace=0.1,wspace=0.1))
    for i,ax in enumerate(axes.flat):
        ax.imshow(faces[i].reshape(62,47),cmap='bone')
    plt.show()
    
plot_faces(example_faces)

在这里插入图片描述

上面就是我们随机选出的36张脸。

特征脸

下面就来看下特征脸是怎样的。

%%time
pca = PCA(svd_solver='randomized')#使用随机的方式求解PCA
pca.fit(X)

在这里插入图片描述

pca.components_.shape

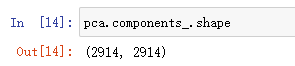
在这里插入图片描述

我们有2914个维度，也就有2914个主成分。

上面我们说过，特征脸就是将主成分中的每一行都当成一个样本，因此我们可以对pca.components_调用绘图方法。

plot_facesd(pca.components_[:36,:])# 取出前36个样本

在这里插入图片描述
这就是特征脸(有点恐怖。。)，从这些特征脸中可以看到，排前面的这些特征脸比较抽象，
排在第一的特征脸好像是说人脸大概的样子和位置。越往后这些脸的五官信息就清晰起来。

我们通过求出特征脸，一方面我们可以直观的看出来在人脸识别中每张脸相应的特征是怎样的；另一方面其实每个人脸都是这些特征脸的线性组合。

参考

1.Python3入门机器学习

愤怒的可乐 博客专家
原创文章 176 获赞 286 访问量 18万+
关注 私信

猜你喜欢

转载自blog.csdn.net/yjw123456/article/details/105927925
今日推荐
TIOBE 5 月榜单：Fortran “复活”进入 Top 10
GCC 14.1 发布
面壁智能发布 Eurux-8x22B 开源大模型 —— 堪称「理科状元」
开源日报 | 谷歌扶持鸿蒙上位；开源Rabbit R1；Docker加持的安卓手机；微软的焦虑和野心；海尔电器把开放平台关了
中国码农的“35岁魔咒”
蘭雅 CorelDRAW 插件 2024.5.1 国际劳动节版，免费下载
Arc Browser for Windows 1.0 正式 GA
90后程序员开发视频搬运软件、不到一年获利超 700 万，结局很刑！
周排行
基本数据类型封装类比较 Java源码解读(一) 8种基本类型对应的封装类型
JS实现无缝滚动上
深入解析HashMap原理（基于JDK1.8）
mysql的连接池
关于.htc
linux下的ubuntu12.04图形界面
【数论】好推不好记的扩展欧几里德
设备树详解
cscope + tags 简单设置
xml学习
每日归档
更多
2024-05-09(35)
2024-05-08(42)
2024-05-07(14)
2024-05-06(40)
2024-05-05(0)
2024-05-04(7)
2024-05-03(19)
2024-05-02(0)
2024-05-01(4)
2024-04-30(1)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022