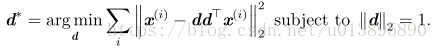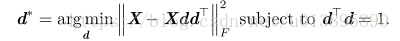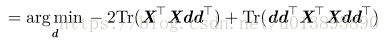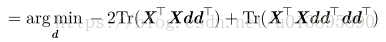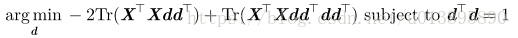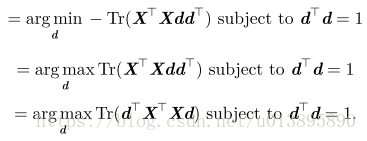问题:假设在空间中我们有 m 个点{
},我们希望对这些点进行有损压缩。
方法:
低维表示:
点 → 编码向量
若,则我们便使用了更少的内存来存储原来的数据。
to find 编码器
and 解码器
令 ,
解码矩阵 (简化解码器)
限制:D的列向量都有单位范数 (为了获得唯一解)
限制:PCA 限制 D 的列向量彼此正交 (简化解码器的最优编码问题)
解最优编码问题:
扫描二维码关注公众号,回复:
2867438 查看本文章


思路:最小化原始输入向量 x 和重构向量g(c)之间的距离。
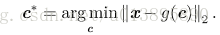
推导:
(若A为单位正交矩阵,则)
则,
。
挑选编码矩阵D:
回顾问题:最小化原始输入向量 x 和重构向量g(c)之间的距离。
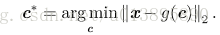
此时可写作:
为了推导用于寻求的算法,我们首先考虑 l = 1 的情况。
此时D是一个向量d,问题变成:
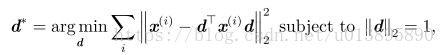
写在左边)
或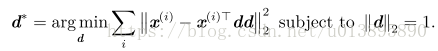
将表示各点的向量按行堆叠成一个矩阵X,则问题又变成

(迹运算性质: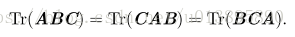
问题变成:
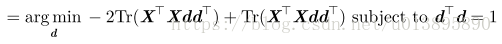
这个优化问题可以通过特征分解来求解。具体来讲,最优的 d 是最大特征值对应的特征向量。
(原理见“特征分解”一节:

以上推导特定于 l = 1 的情况,仅得到了第一个主成分。
更一般地,当我们希望得到主成分的基时,矩阵 D 由前 l 个最大 的特征值对应的特征向量组成。
这个结论可以通过归纳法证明。
参考:机器学习花书