参见:https://blog.csdn.net/program_developer/article/details/80632779
一.概述
1.概念:
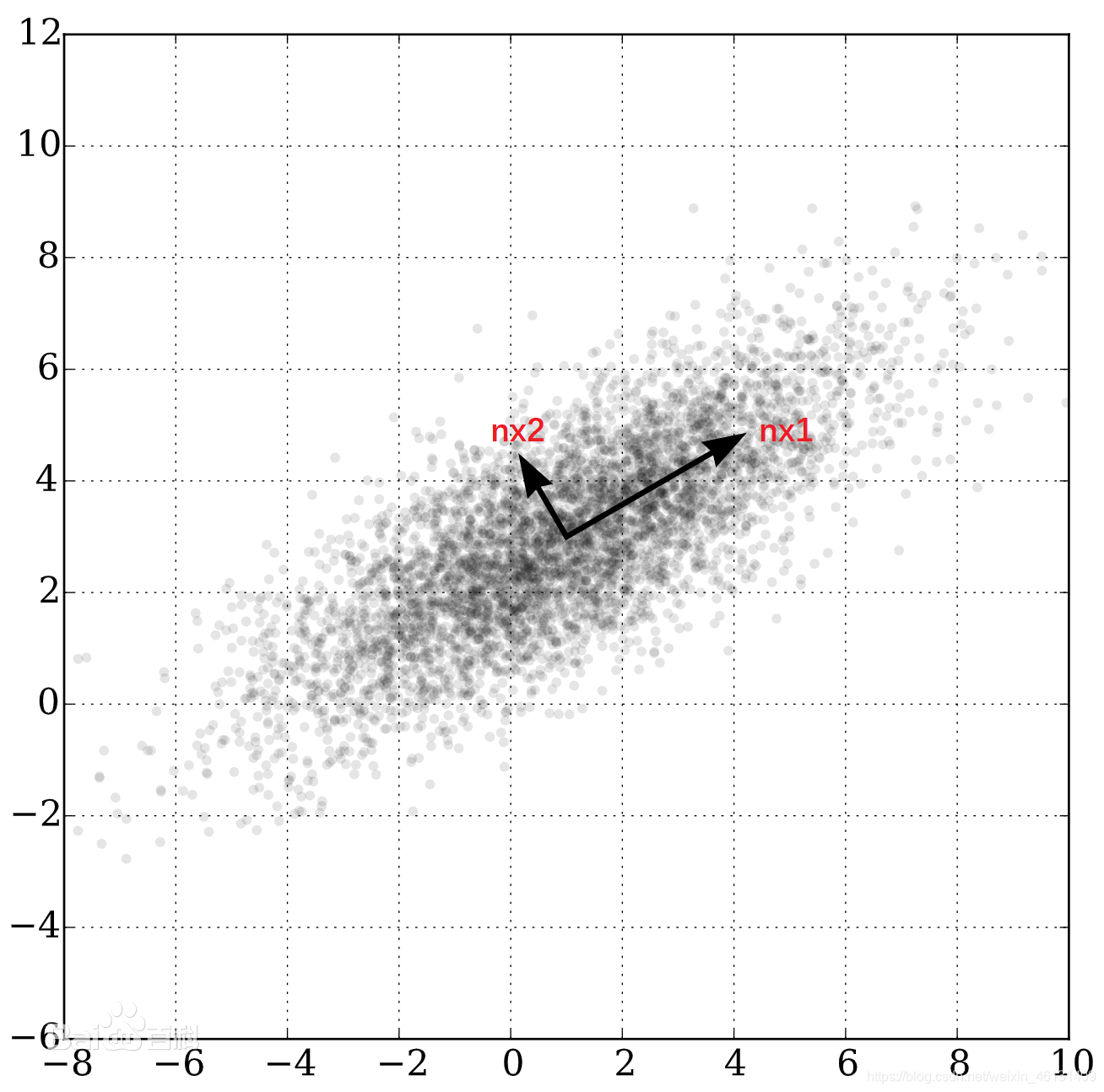
"主成分分析"(Principal Component Analysis;PCA)的主要思想是将n维特征映射到k维上.这k维是全新的正交特征,称为"主成分",是在原有n
维特征的基础上重新构造出来的.形象地说,PCA就是在原特征空间中找到1组相互正交的轴.其中,第1个新轴是原始数据中方差最大的方向,第2个新轴
是与第1个坐标轴正交的平面中方差最大的方向...以此类推.计算方法为:计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值和特征向量,选择
对应的特征值最大(即方差最大)的k个特征向量,由这些向量张成新的特征空间.由于有2种方法可以特征值和特征向量:特征分解和奇异值分解阵,所以
PCA有两种实现:"基于特征分解协方差矩阵的PCA"和"基于SVD分解协方差矩阵的PCA"
2.功能:
①降维,减少计算开销
②便于可视化
③去除噪声,避免过拟合
④发现更容易被人理解的特征
二.实现
1.原理:
基于特征分解协方差矩阵的PCA:
①设原始变量 X 1 , X 2 … X p X_1,X_2…X_p X1,X2…Xp的 n n n次观测数据矩阵为 X = [ x 11 . . . x 1 p . . . . . . . . . x n 1 . . . x n p ] = [ X 1 , X 2 . . . X p ] ( 1 ) X=\left[\begin{matrix}x_{11}&...&x_{1p}\\...&...&...\\x_{n1}&...&x_{np}\end{matrix}\right]=\left[\begin{matrix}X_1,X_2...X_p\end{matrix}\right]\qquad(1) X=⎣⎡x11...xn1.........x1p...xnp⎦⎤=[X1,X2...Xp](1)
②对数据矩阵按列进行标准化,结果仍记为 X X X
③求相关系数矩阵 R = ( r i j ) p R=(r_{ij})_p R=(rij)p
④求解 R R R的特征方程 ∣ R − λ E ∣ = 0 |R-λE|=0 ∣R−λE∣=0,特征根为 λ 1 ≥ λ 2 ≥ . . . ≥ λ p > 0 λ_1≥λ_2≥...≥λ_p>0 λ1≥λ2≥...≥λp>0
⑤确定主成分个数 m m m,使 ∑ i = 1 m λ i ∑ i = 1 p λ i ≥ α \frac{\displaystyle\sum_{i=1}^mλ_i}{\displaystyle\sum_{i=1}^pλ_i}≥α i=1∑pλii=1∑mλi≥α其中 α α α需根据实际情况确定,通常取 80 % 80\% 80%
⑥找到最大的 m m m个特征值对应的单位特征向量 β 1 = [ β 11 . . . β p 1 ] , β 2 = [ β 12 . . . β p 2 ] . . . β 1 = [ β 1 m . . . β p m ] ( 2 ) β_1=\left[\begin{matrix}β_{11}\\...\\β_{p1}\end{matrix}\right],β_2=\left[\begin{matrix}β_{12}\\...\\β_{p2}\end{matrix}\right]...β_1=\left[\begin{matrix}β_{1m}\\...\\β_{pm}\end{matrix}\right]\qquad(2) β1=⎣⎡β11...βp1⎦⎤,β2=⎣⎡β12...βp2⎦⎤...β1=⎣⎡β1m...βpm⎦⎤(2)
⑦求主成分 Z i = β 1 i X 1 + . . . + β p i X p ( i = 1 , 2... m ) Z_i=β_{1i}X_1+...+β_{pi}X_p\,(i=1,2...m) Zi=β1iX1+...+βpiXp(i=1,2...m)
2.实现: