机器学习系列-主成分分析

PCA

降维

一些机器学习算法在处理高维数据时，性能会出现明显下降，这就是所谓的“维度灾难”，为此人们开始对算法进行改进。与此同时，对降维的需求催生了降维算法，比如本文要介绍的主成分分析（Principal Component Analysis，PCA）。

在开始本文的主要内容之前，我想先举一个关于降维的例子：

有5个点，坐标如下表所示：

id	x	y
1	5.0	1.4
2	5.0	2.3
3	5.0	5.6
4	4.9	7.8
5	5.0	11.1

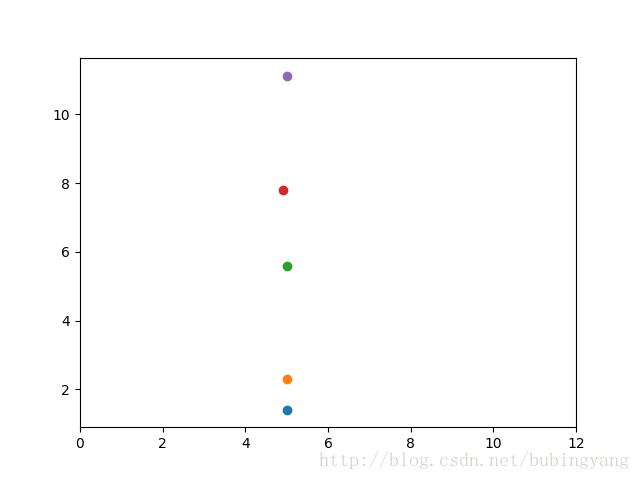
将他们画在图中：

虽然是二维空间中的点，但是这些点的横坐标几乎都是5，只有第4个点的横坐标稍稍有些“不合群”，我们不妨将这0.1(5-4.9)的偏差作为噪声略去，这样所有的点横坐标都相同了。

现在我们从坐标的角度去分析这些点的差异性，就会发现，分析横坐标是没有任何意义的，因为所有的点横坐标都相等。忽略了横坐标，分析这些二维空间上点等同于分析一维数轴上的点，过程简单了许多。这就是一个降维的过程。

主成分分析（PCA）

上述的降维方法其实是将二维的点全部投影到y轴上，但这样有个问题，这种投影方式不能将不同的数据的差异性体现出来（有些文档也称为变异性）。而PCA要做的就是将数据沿方差最大方向投影，数据更易于区分。详细的说就是，所选取的第一个维要尽可能多的捕获数据的差异性，第二个维与前面的维正交，使得与第一个维一起变化的程度最小，并尽可能多的捕获剩余的差异性，然后继续下去。接下来我们详细介绍PCA的原理。

概率论中通过计算数据的协方差矩阵$S$汇总多元数据集(例如，具有多个连续属性的数据)的差异性。

给定一个$m*n$的数据矩阵$D$，其$m$个行是数据对象，其$n$个列是属性。$D$的协方差矩阵为$S$，其元素$s_{ij}$定义为$s_{ij}=covariance(d_{*i},d_{*j})$

换言之，$s_{ij}$是数据第$i$个和第$j$个属性的协方差。

两个属性的协方差度量两个属性一起变化的程度。如果$i=j$（即两个属
性相同），则协方差就是该属性的方差。如果数据矩阵$D$经过预处理，使得每个属性的均值都是$0$,则$S=\frac{1}{m}DD^{T}$。

前面说过，PCA有一个目标，就是使不同属性之间协同变化的程度最小，在这里体现为要将协方差矩阵对角化，并且对角线上的元素按照从大到小排列。

设原始数据矩阵$D$对应的协方差矩阵为$S$，而$P$是一组基按行组成的矩阵，设$D'=PD$，则$D'$为$P$对$D$做基变换后的数据。设$D'$的协方差矩阵为$S'$，$S$与$S'$的关系：

$$S'=\frac{1}{m}D'D'^{\ T}=\frac{1}{m}(PD)(PD)^T=\frac{1}{m}PDD^TP^T=P(\frac{1}{m}DD^T)P^T=PSP^T$$

现在目标变成了寻找一个矩阵$P$，满足$PSP^{T}$是一个对角矩阵，并且对角元素按从大到小依次排列，那么$P$的前$K$行就是要寻找的基，用$P$的前$K$行组成的矩阵乘以$D$就使得$D$从$N$维降到了$K$维并满足优化条件。

协方差矩阵$S$是一个是对称矩阵，在线性代数上，实对称矩阵有一系列非常好的性质：

1. 实对称矩阵不同特征值对应的特征向量必然正交。

2. 设特征向量$\lambda$重数为$r$，则必然存在$r$个线性无关的特征向量对应于$\lambda$，因此可以将这$r$个特征向量单位正交化。

由上面两条可知，一个$n$行$n$列的实对称矩阵一定可以找到$n$个单位正交特征向量，设这$n$个特征向量为$e_1,e_2,\cdots,e_n$，我们将其按列组成矩阵：

$$E=(e_1,e_2,\cdots ,e_n)$$

则对协方差矩阵$S$有如下结论：

$$E^TCE=\Lambda=\begin{pmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \end{pmatrix}$$

到这里，我们发现我们已经找到了需要的矩阵$P$：

$$P=E^\mathsf{T}$$

$P$是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是$S$的一个特征向量。如果设$P$按照$\Lambda$中特征值的从大到小，将特征向量从上到下排列，则用$P$的前$k$行组成的矩阵乘以原始数据矩阵$D$，就得到了我们需要的降维后的数据矩阵$D'$。

主成分分析的优缺点

主成分分析的优点

1. 以方差衡量信息的无监督学习，不受样本标签限制。
2. 各主成分之间正交，可消除原始数据成分间的相互影响。
3. 可减少指标选择的工作量。
4. 有一定的降噪效果。

主成分分析的缺点

1. 主成分解释其含义往往具有一定的模糊性。
2. 贡献率小的主成分往往可能含有对样本差异的重要信息。
3. PCA降维属于有损压缩，降维后的数据不如原始数据完整。