【笔记】向量和矩阵的0、1、2、无穷、p、f、核范数
其他
2020-04-24 12:00:52
阅读次数: 0
0范数：
含义： 非0元素的个数
1范数：
向量： 
，所有元素的绝对值之和
矩阵：
,即矩阵列向量之和的绝对值的最大值
2范数：
向量：
，即平方和再开放
矩阵：
为
的最大特征值
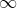范数：
向量：
，即最大的绝对值
矩阵：
，即矩阵行向量和的绝对值的最大值
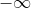范数：
向量：
，即最小的绝对值
P范数：
向量：
，类似2范数，为所有元素的p次方和开p次方
F范数：
矩阵： 
，即所有元素平方和再开方
核范数：
矩阵：
为A的奇异值，即奇异值之和
发布了138 篇原创文章 ·
获赞 13 ·
访问量 2452
转载自blog.csdn.net/songyuwen0808/article/details/105655292
