非线性规划：实例与matlab应用

一般非线性规划
标准型为：
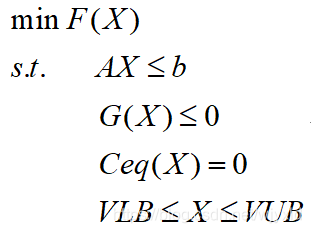
在这里插入图片描述
其中X为n维变元向量，G(X)与Ceq(X)均为非线性函数组成的向量，其它变量的含义与线性规划、二次规划中相同.
matlab中非线性规划求解的函数是fmincon,命令的基本格式如下：
 x=fmincon(‘fun’,X0,A,b)
 x=fmincon(‘fun’,X0,A,b,Aeq,beq)
 x=fmincon(‘fun’,X0,A,b, Aeq,beq,VLB,VUB)
 x=fmincon(‘fun’,X0,A,b,Aeq,beq,VLB,VUB,’nonlcon’)
 x=fmincon(‘fun’,X0,A,b,Aeq,beq,VLB,VUB,’nonlcon’,options)
 [x,fval]= fmincon(…)
 [x,fval,exitflag]= fmincon(…)
 [x,fval,exitflag,output]= fmincon(…)
1.fun为目标函数
2.x0为初始值
3.A是不等式约束AX<=b的系数矩阵
4.b是不等式约束AX<=b的常数项
4.Aeq是等式约束AeqX=beq的系数矩阵，
5.beq是等式约束AeqX=beq的常数项，
6.lb是X的下限，
7.ub是X的上限，
8.nonlcon为非线性不等式约束
9.option为设置fmincon的参数
注意：
fmincon函数提供了大型优化算法和中型优化算法。默认时，若在fun函数中提供了梯度（options参数的GradObj设置为’on’），并且只有上下界存在或只有等式约束，fmincon函数将选择大型算法。当既有等式约束又有梯度约束时，使用中型算法。
fmincon函数的中型算法使用的是序列二次规划法。在每一步迭代中求解二次规划子问题，并用BFGS法更新拉格朗日Hessian矩阵。
fmincon函数可能会给出局部最优解，这与初值X0的选取有关。

实例：供应与选址
某公司有6个建筑工地要开工，每个工地的位置（用平面坐标系a，b表示，距离单位：千米）及水泥日用量d(吨)由下表给出。目前有两个临时料场位于A(5,1)，B(2,7)，日储量各有20吨。假设从料场到工地之间均有直线道路相连。
（1）试制定每天的供应计划，即从A，B两料场分别向各工地运送多少吨水泥，使总的吨千米数最小。
（2）为了进一步减少吨千米数，打算舍弃两个临时料场，改建两个新的，日储量各为20吨，问应建在何处，节省的吨千米数有多大？
在这里插入图片描述

当用临时料场时决策变量为：xij，当不用临时料场时决策变量为：xij，xj，yj。

情形2：使用临时料场的情形
使用两个临时料场A(5,1)，B(2,7).求从料场j向工地i的运送量为Xij，在各工地用量必须满足和各料场运送量不超过日储量的条件下，使总的吨千米数最小，这是线性规划问题. 线性规划模型为：
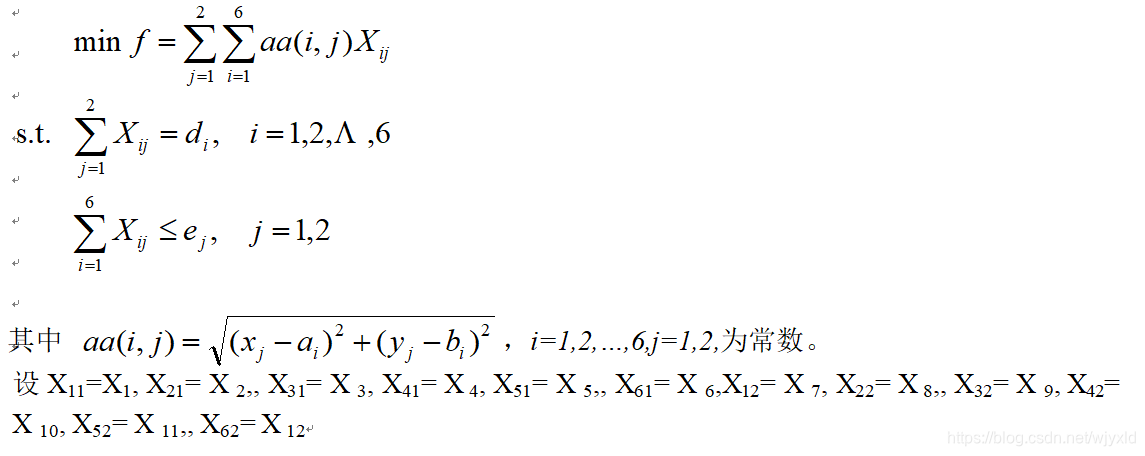
在这里插入图片描述
Matlab程序

clear
a=[1.25 8.75 0.5 5.75 3 7.25];
b=[1.25 0.75 4.75 5 6.5 7.75];
d=[3 5 4 7 6 11];
x=[5 2];
y=[1 7];
e=[20 20];
for  i=1:6
   for j=1:2
      aa(i,j)=sqrt((x(j)-a(i))^2+(y(j)-b(i))^2);
   end
end
CC=[aa(:,1); aa(:,2)]';
A=[1 1 1 1 1 1 0 0 0 0 0 0
   0 0 0 0 0 0 1 1 1 1 1 1];
B=[20;20];
Aeq=[1 0 0 0 0 0 1 0 0 0 0 0
    0 1 0 0 0 0 0 1 0 0 0 0 
    0 0 1 0 0 0 0 0 1 0 0 0 
    0 0 0 1 0 0 0 0 0 1 0 0 
    0 0 0 0 1 0 0 0 0 0 1 0 
    0 0 0 0 0 1 0 0 0 0 0 1 ];
beq=[d(1);d(2);d(3);d(4);d(5);d(6)];
VLB=[0 0 0 0 0 0 0 0 0 0 0 0];VUB=[];
x0=[1 2 3 0 1 0 0 1 0 1 0 1];
[xx,fval]=linprog(CC,A,B,Aeq,beq,VLB,VUB,x0)

计算结果为：
x =[ 3.0000  5.0000  0.0000  7.0000  0.0000  1.0000  
0.0000  0.0000  4.0000   0.0000  6.0000 10.0000]’
fval = 136.2275

情形3：改建两个新料场的情形
改建两个新料场，要同时确定料场的位置(xj,yj)和运送量Xij，在同样条件下使总吨千米数最小。这是非线性规划问题。非线性规划模型为：
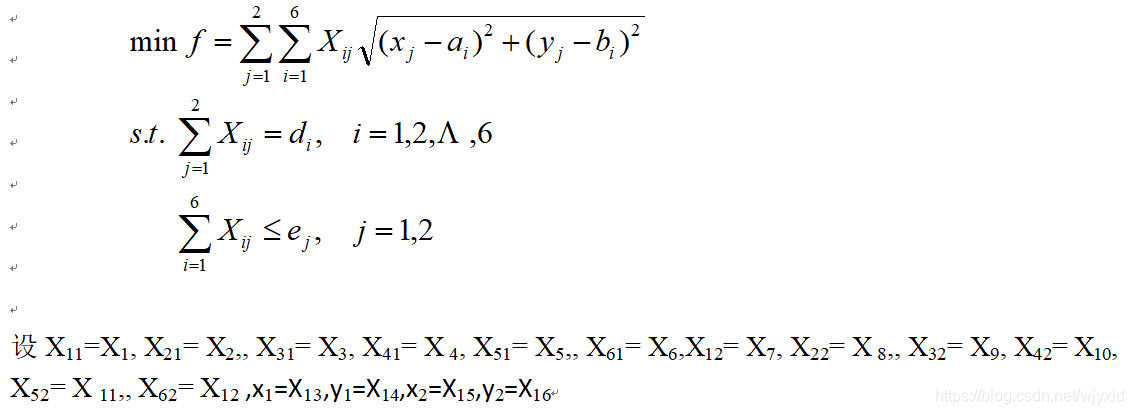
在这里插入图片描述

function f=ex5(x)
a=[1.25 8.75 0.5 5.75 3 7.25];
b=[1.25 0.75 4.75 5 6.5 7.75];
d=[3 5 4 7 6 11];
e=[20 20];
f1=0;
for  i=1:6
   s(i)=sqrt((x(13)-a(i))^2+(x(14)-b(i))^2);
   f1=s(i)*x(i)+f1;
end
f2=0;
for  i=7:12
   s(i)=sqrt((x(15)-a(i-6))^2+(x(16)-b(i-6))^2);
   f2=s(i)*x(i)+f2;
end
f=f1+f2;

取初值为线性规划的计算结果及临时料场的坐标:
x0=[3 5 0 7 0 1 0 0 4 0 6 10 5 1 2 7]’;

clear;
%x0=[3  5 0  7  0  1  0  0  4  0  6 10 5 1 2 7]';
%x0=[ 3.0000    5.0000    0.0707    7.0000         0    0.9293    0         0    3.9293         0    6.0000   10.0707   6.3875    4.3943    5.7511    7.1867]';
%x0=[ 3.0000    5.0000    0.3094    7.0000    0.0108    0.6798      0         0    3.6906         0    5.9892   10.3202  5.5369    4.9194    5.8291    7.2852]';
x0=[3 5 4 7 1 0 0 0 0 0 5 11 5.6348 4.8687 7.2479 7.7499]';
A=[1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0];
B=[20;20];
Aeq=[1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
    0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 
    0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0
    0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0
    0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0
    0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0];
beq=[3 5 4 7 6 11]';
vlb=[zeros(12,1);-inf;-inf;-inf;-inf];
vub=[];
[x,fval,exitflag]=fmincon('ex5',x0,A,B,Aeq,beq,vlb,vub)

计算结果为：
x=[ 3.0000 5.0000 0.0707 7.0000 0 0.9293
0 0 3.9293 0 6.0000 10.0707
6.3875 4.3943 5.7511 7.1867]’
fval = 105.4626
exitflag = 1

即两个新料场的坐标分别为(6.3875, 4.3943),(5.7511, 7.1867).

xuelida

发布了55 篇原创文章 · 获赞 80 · 访问量 3775

私信关注

非线性规划：实例与matlab应用

猜你喜欢