线性规划及matlab应用

1. 线性规划的 Matlab 标准形式
2. 可以转化为线性规划的问题
3. 取最大或最小值的“伪线性规划”问题
4. 模型中某些变量没有非负限制
5. 实例：连续投资问题

在人们的生产实践中，经常会遇到如何利用现有资源来安排生产，以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支—数学规划，而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。自从1947 年G. B. Dantzig 提出求解线性规划的单纯形方法以来，线性规划在理论上趋向成熟，在实用中日益广泛与深入。特别是在计算机能处理成千上万个约束条件和决策变量的线性规划问题之后，线性规划的适用领域更为广泛了，已成为现代管理中经常采用的基本方法之一。
线性规划问题是在一组线性约束条件的限制下，求一线性目标函数最大或最小的问题。在解决实际问题时，把问题归结成一个线性规划数学模型是很重要的一步，但往往也是困难的一步，模型建立得是否恰当，直接影响到求解。而选适当的决策变量，是我们建立有效模型的关键之一。

1.线性规划的 Matlab 标准形式
线性规划的目标函数可以是求最大值，也可以是求最小值，约束条件的不等号可以是小于号也可以是大于号。为了避免这种形式多样性带来的不便，Matlab 中规定线性规划的标准形式为


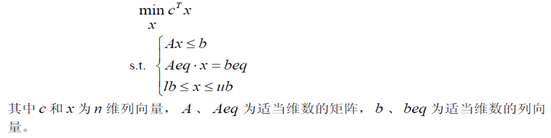
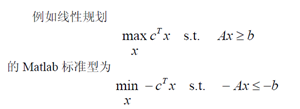
Matlab线性规划的基本函数形式为 linprog(c,A,b)，它的返回值是向量x 的值。还有其它的一些函数调用形式（在 Matlab 指令窗运行 help linprog 可以看到所有的函数调用形式），如：
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)
这里fval 返回目标函数的值，LB 和UB 分别是变量x 的下界和上界，x0 是x 的初始值，
OPTIONS 是控制参数。
例1：

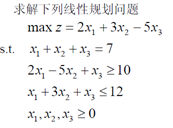
matlab命令

c=[2;3;-5];
a=[-2,5,-1;1,3,1]; b=[-10;12];
aeq=[1,1,1];
beq=7;
x=linprog(-c,a,b,aeq,beq,zeros(3,1))
value=c'*x

例2：求解线性规划问题

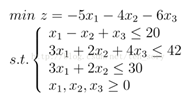
f=[-5,-4,-6];
a=[1,-1,1;3,2,4;,3,2,0];
b=[20;42;30];
lb=zeros(3,1);
[x,y]=linprog(f,a,b,[],[],lb)

2. 可以转化为线性规划的问题
   很多看起来不是线性规划的问题也可以通过变换变成线性规划的问题来解决。如：规划问题为，
   
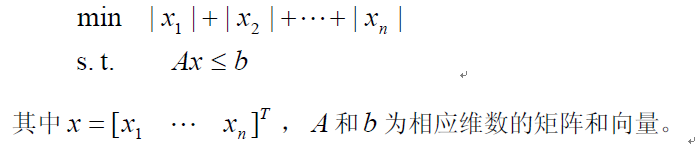
   要把上面的问题变换成线性规划问题，只要注意到事实：对任意的xi，存在
   
   例3：求解线性规划问题
   
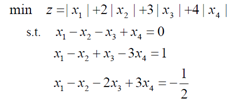
   对任意的xi，存在ui,vi>0,满足xi=ui-vi；|xi|=ui+vi；
   则上面的优化问题转化为：
   
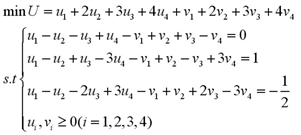
   matlab命令

clc,clear;
c=[1,2,3,4,1,2,3,4];
Aeq=[1,-1,-1,1,-1,1,1,-1;1,-1,1,-3,-1,1,-1,3;1,-1,-2,3,-1,1,2,-3];
beq=[0;1;-1/2];
lb=zeros(8,1);
uv0=ones(8,1);
options = optimset('LargeScale', 'off', 'Simplex', 'on','Diagnostics','on','MaxIter',1000);
[uv,fval,exitflag,output,lambda]=linprog(c,[],[],Aeq,beq,lb,[],uv0,options)

解得u1,u2,u3,u4,v1,v2,v3,v4分别为：1/4,0,0,0,0,0,0,1/4,即 x1,x2,x3,x4的值分别为：1/4,0,0,-1/4时，最小者为1.25。

3. 取最大或最小值的“伪线性规划”问题
   例4：问题可以描述为：
   
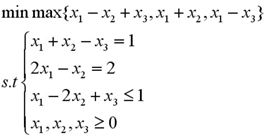
   现令x0=max{x1-x2+x3，x1+x2,x1-x3},故有
   x0>=x1-x2+x3,x0>=x1+x2,x0>=x1-x3
   故上面的规划问题转换为：
   
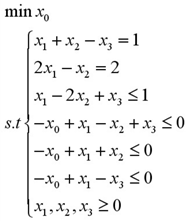
   matlab命令

clear;
clc;
c=[1,0,0,0];
Aeq=[0,1,1,-1;0,2,-1,0];
beq=[1;2];
A=[0,1,-2,1;-1,1,-1,1;-1,1,1,0;-1,1,0,-1];
b=[1;0;0;0];
lb=zeros(3,1);
xx0=[-inf;0;0;0];
options = optimset('LargeScale', 'off', 'Simplex', 'on','Diagnostics','on','MaxIter',1000);
[x,fval,exitflag,output,lambda]=linprog(c,A,b,Aeq,beq,lb,[],xx0,options)

运行结果：x1,x2,x3分别为：1,0,0时，取得最优解为1。

4. 模型中某些变量没有非负限制
   
   
5. 实例：连续投资问题
   某机构将200万元进行投资，共有4个方案可供选择，投资的方式为每年年初将机构持有的所有资本都用于投资。
   方案1：从第1年年末第4年的每年年初都投资，次年年末收获本利1.15
   方案2：第3年年初投资，到第5年年末收回本利1.25，最大投资额80万元
   方案3：第2年年初投资，到第5年年末收回本利1.4，最大投资额60万元
   方案4：每年年初投资，每年年末收回本利1.06
   问采取何种投资组合策略，使得第5年年末的总资本最大。
   
   可以得到该问题的线性规划描述
   
   Matlab程序如下：

clear;clc;
c=[0 0 0 -1.4 0 0 -1.25 0 -1.15 0 -1.06]
Aeq=[1 1 0 0 0 0 0 0 0 0 0
     0 1.06 -1 -1 -1 0 0 0 0 0 0
     1.15 0 0 0 1.06 -1 -1 -1 0 0 0
     0 0 1.15 0 0 0 0 1.06 -1 -1 0
     0 0 0 0 0 1.15 0 0 0 1.06 -1]
beq=[200 0 0 0 0]
lb=[0 0 0 0 0 0 0 0 0 0 0]
ub=[Inf Inf Inf 60 Inf Inf 80 Inf Inf Inf Inf]
[x,fval]=linprog(c,[],[],Aeq,beq,lb,ub)

运行结果
x = 123.5459
76.4541
21.0414
60.0000
0.0000
34.5138
80.0000
27.5639
53.4154
0.0000
39.6909

fval = -287.5000

采取上述最佳投资方案后，在第5年年末所得到的总资本数为287.5万元