多目标规划模型
多目标规划模型的基本知识
前面介绍的线性规划模型、整数规划模型、非线性规划模型中的目标函数都只有一个（可以进我的博客查看详细）。而在许多实际问题中，衡量一个方案好坏的标准往往不止一个，例如设计导弹，既要射程最远，又要燃料最省，还要精度最高。这一类问题称为多目标规划问题。对多目标规划问题建立其具有多个目标函数的数学规划模型称为多目标规划模型。
具有个目标的多目标规划模型的一般形式为：
目标函数：
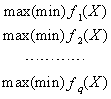
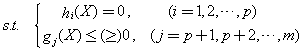
由于等式约束总可以转化为不等式约束，大于等于约束总可以转化为小于等于约束，同时目标函数的最大化总可以转化为目标函数的最小化，于是多目标规划模型的一般形式又可简化为：
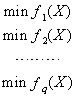
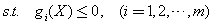
称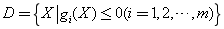
为多目标规划模型的可行域。多目标规划模型的一般形式又可表达为：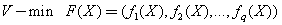
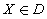
其中V-min表示对个目标f1(X)，f2(X)，…，fq(X)以追求最小为目的。
设有两向量
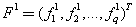
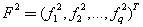
规定以下几个有关向量比较的符号：
（1）符号“≤”：若 F1≤F2，则意味着F1的每个分量都要小于或等于F2的对应的分量；
（2）符号“<”：若F1<F2，则意味着F1的每个分量都要严格小于F2的对应的分量；
（3）符号“≤”：若 F1≤F2，则意味着F1的每个分量都要小于或等于F2的对应的分量，并且存在F1的某一个分量严格的小于F2的对应的分量。
多目标规划模型的绝对最优解
多目标规划模型的有效解
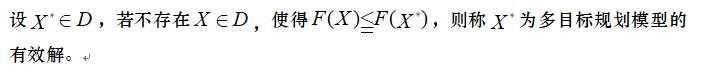
多目标规划模型的弱有效解
在多目标规划模型的个目标中，有的相互联系，有的相互制约，有的相互冲突。多目标规划模型除了目标函数不只一个这一明显的特点外，最显著的还有以下两点：目标间的不可公度性和目标间的矛盾性。
-
目标间的不可公度性
目标间的不可公度性是指各个目标没有统一的度量标准，因而难以直接进行比较。例如房屋设计问题中，造价目标的单位是元/平方米，建造时间目标的单位是年，而结构、造型等目标则为定性指标； -
目标间的矛盾性
目标间的矛盾性是指如果选择一种方案以改进某一目标的值，可能会使另一目标的值变坏，如房屋设计中造型、抗震性能目标的提高可能会使房屋建造成本目标提高。正是由于目标间的矛盾性，解决实际问题所建立的多目标规划模型常常没有绝对最优解，只能寻找其有效解或弱有效解。
多目标规划模型的常用解法介绍
多目标规划模型的解法大致可分为两类：直接解法和间接解法。到目前为止，常用的多为间接解法，即根据问题的实际背景和特征，设法将多目标规划模型转化为单目标规划模型，从而得到多目标规划模型的满意解。
1. 主要目标法
在多目标规划模型中，若能从q个目标中，确定一个目标为主要目标，例如f1(X)，而把其余目标作为次要目标，并根据实际情况，确定适当的界限值，这样就可以把次要目标作为约束来处理，而将多目标规划模型转化为求解如下的单目标线性或非线性规划模型：
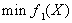
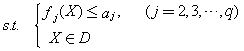
其中界限值取为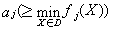
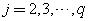
则此单目标规划模型的最优解必为原多目标规划模型的弱有效解。因此，用主要目标法求得的解必是多目标规划模型的弱有效解或有效解。
2. 分层序列法
把多目标规划模型中的q个目标按其重要程度排一个次序，假设f1(X)最重要，f2(X)次之 ，f3(X)再次之，… ，最后一个目标为fq(X)。
先求出以第一个目标f1(X)为目标函数，而原模型中的约束条件不变的问题P1：
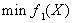
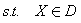
其最优解为X1，最优值为f1*。再求解问题P2：
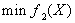
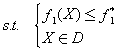
其最优解为X2，最优值为f2*。再求解问题P3：
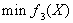
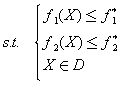
其最优解为X3，最优值为f3*，… ，如此继续下去，直到求解第q个问题Pq：
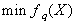
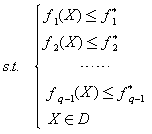
其最优解为Xq，最优值为fq*。则X*=Xq就是原多目标规划模型在分层序列意义下得最优解，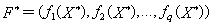
为其最优值。
常将分层序列法修改如下：选取一组适当小的正数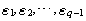
成为宽容值，把上述的问题Pj修改如下：
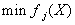
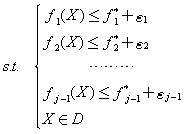
再按上述方法依次求解各问题P1,P2,…,Pq 。
3．线性加权求和法
对多目标规划模型中的q个目标按其重要程度给以适当的非负权系数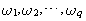
且
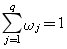，然后用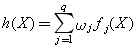
作为新的目标函数，成为评价（目标）函数，再求解单目标规划问题：
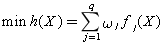
多目标规划建模示例
选课策略问题
某学校规定，运筹学专业的学生毕业时必须至少学习两门数学课程、三门运筹学课程和两门计算机课程。这些课程的编号、名称 、学分、所属类别和先修课程要求如表所示。一般学生选课时要考虑总的课程门数和所获得的学分。试设计选课策略，在满足毕业要求的同时，使得所修课程门数尽量少，所获得的学分尽量多。
1. 模型假设
（1）各个同学在选课时不受其他因素影响，只受学分和选课门数影响；
（2）各门课程没有人数限制；
（3）仅考虑表所列9门课程。
2. 模型建立
（1）决策变量
定义如下0-1变量作为决策变量：
（2）约束条件
至少选两门数学课程、三门运筹学课程和两门计算机课程，根据表中对各门课程所属类别的划分，这一约束可以表示为：
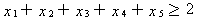
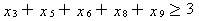
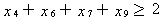
某些课程有先修课程的要求。例如“数据结构”的先修课是“计算机编程”，这意味着如果x4=1，必须x7=1，这个条件可以表示为x4≤x7（注意：x4=0时对x7没有限制）。“最优化方法”的先修课是“微积分”和“线性代数”这一条件可以表示为x3≤x1，x3≤x2，而这两个不等式可以合并为2x3-x1-x2≤0。这样，所有课程的先修课要求可以表达为：
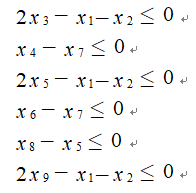
（3）目标函数
根据本问题的假设，我们考虑课程门数和学分两个目标。
所选课程门数可表达为：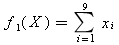
我们希望课程门数尽量少，即希望对目标函数f1(X)实现最小化。
所选课程的总学分可表达为：
其中λi为课程编号为i的课程的学分，这里λ1=5,λ2=4,λ3=4,λ4=3,λ5=4,λ6=3,λ7=2,λ8=2,λ9=3。
我们希望学分尽量多，即希望对目标函数f2(X)实现最大化。
综合上述分析，选课策略问题的数学模型为如下多目标规划模型：
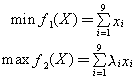
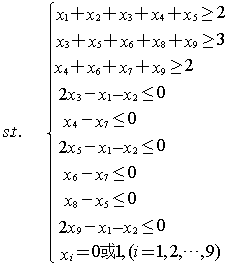
3. 模型求解
记上述多目标规划模型的可行域为D。
（1）如果以课程门数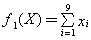
作为主要目标，不考虑学分的多少，由主要目标法将上述多目标规划模型转化为如下的单目标规划模型：
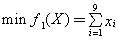
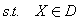
运用LINGO软件求解得到：
x1=x2=x3=x6=x7=x9=1; x4=x5=x8=0
即选微积分、线性代数、最优化方法、计算机模拟、计算机编程、数学实验这6门课，可满足毕业要求并使课程门数最少，此时总学分为21。
（2）如果以课程门数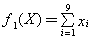
作为最重要目标，总学分
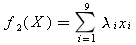作为次重要目标，即在课程门数达到最少的前提下使总学分达到最多。于是利用分层序列法在上述的基础上，再次求解如下的单目标规划模型：
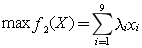
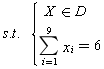
运用LINGO软件求解得到：
x1=x2=x3=x5=x7=x9=1; x4=x6=x8=0
即将上述（1）中学分的“计算机模拟”换成4学分的“应用统计”，同样这6门课，可使总学分由21增至22。
（3）如果认为课程门数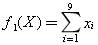
和总学分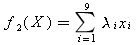
这两个目标的重要程度之间的差异不十分明显，这时可由线性加权求和法取权系数0.7和0.3，将原多目标规划模型转化为如下的单目标规划模型：
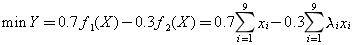
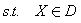
运用LINGO软件求解得到：
x1=x2=x3=x4=x5=x6=x7=x9=1; x8=0
即选微积分、线性代数、最优化方法、数据结构、应用统计、计算机模拟、计算机编程、数学实验这8门课。此时虽然课程门数增加了两门课，但总学分也增加到了28。
有用的话希望小伙伴们来个三连击，这是对我最大的鼓励
也让更多的人能够看到这篇文章！！！
帅气、靓丽的来个赞和关注
帅气、靓丽的来个赞和关注
帅气、靓丽的来个赞和关注
