1、概念

是一种在数学、计算机科学和经济学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划算法是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。

动态规划（Dynamic Programming）对于子问题重叠的情况特别有效，因为它将子问题的解保存在表格中，当需要某个子问题的解时，直接取值即可，从而避免重复计算！

动态规划是一种灵活的方法，不存在一种万能的动态规划算法可以解决各类最优化问题（每种算法都有它的缺陷）。所以除了要对基本概念和方法正确理解外，必须具体问题具体分析处理，用灵活的方法建立数学模型，用创造性的技巧去求解。

2、背包问题

题意： 假设有一个小偷，背着一个4磅东西的背包，假设可盗取如下商品：

商品名	价格	重量
音响	3000 美元	4 磅
笔记本电脑	2000 美元	3 磅
吉他	1500 美元	1 磅

为了让盗窃的商品价值最高，该如何选择哪些商品？

步骤： 对于背包问题，应先解决小背包（子背包）问题，再逐步解决原来的问题。每个动态规划算法都从一个网格开始，其中网格各列为不同容量的背包，各行为可选择的商品。填充的网格大致步骤如下：

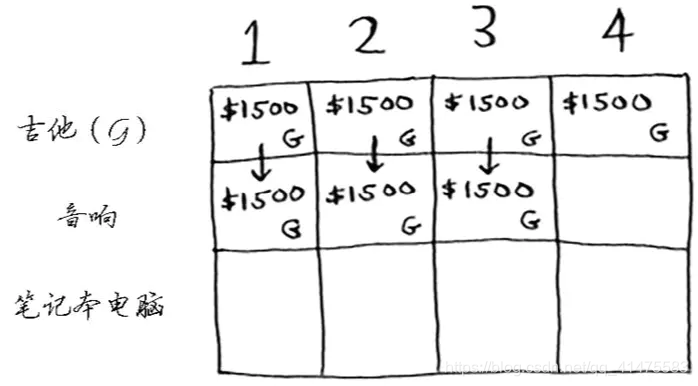
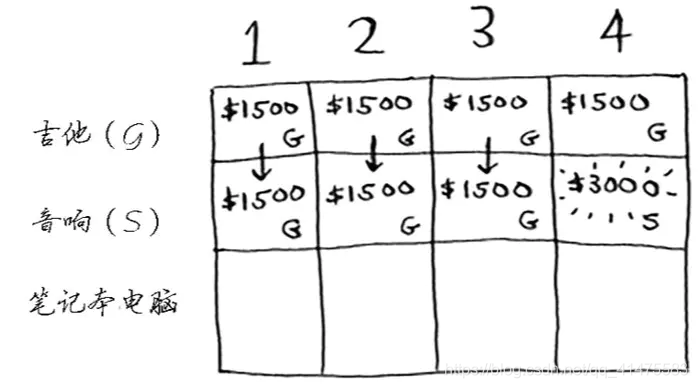
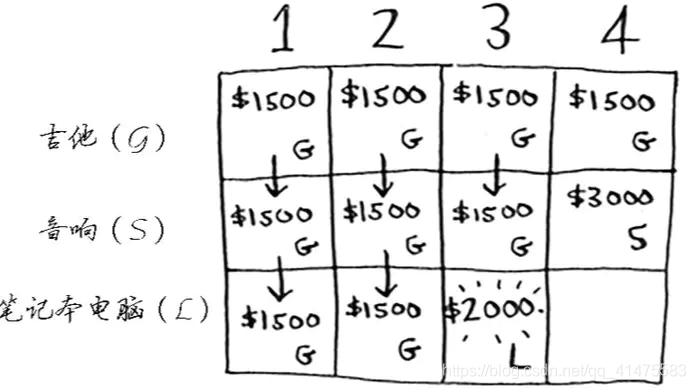
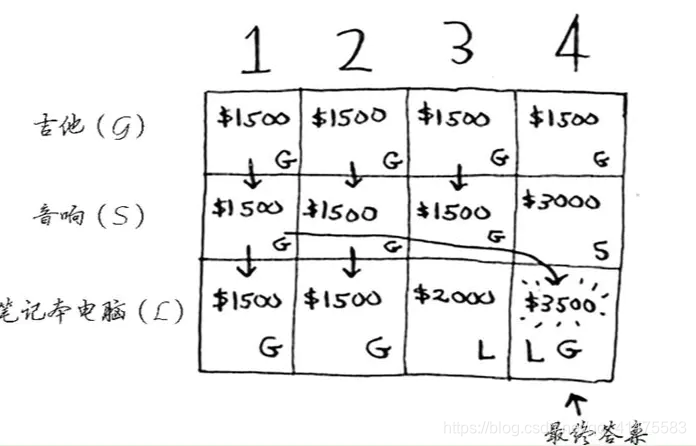
在这里插入图片描述

公式总结为：
$cell[i][j]=两者中较大的那个\begin{cases} & \text{1.}上一个单元格的值(即cell[i-1][j]) \\ & \text{2. } 当前商品的价值+剩余空间的价值(即cell[i-1][j-当前商品的重量]) \end{cases}$
可以使用这个公式来计算每个单元格的价值，最终的网格将与前一个网格相同。

Python源代码

大致思路：
1.通过bag()函数可以生成网格，即可定位出最大价值单元格。
2.最大价值单元格中所选商品一定包括该网格所在行的商品。
3.用最大价值-该行商品价值得到剩余价值，然后遍历网格，挑选出第一次出现剩余价值的单元格，则剩余价值中所选商品一定包括所在行商品。
4迭代步骤3，直至剩余价值==0.

#第一步建立网格(横坐标表示[0,c]整数背包承重):(n+1)*(c+1)
def bag(n,c,w,p):
    res=[[0 for j in range(c+1)]for i in range(n+1)]
    for j in range(c+1):
        #第0行全部赋值为0，物品编号从1开始.为了下面赋值方便
        res[0][j]=0
    for i in range(1 , n+1):
        for j in range(1 ,c+1):
           # print(res[i-1][j])
            res[i][j]=res[i-1][j]
            #生成了n*c有效矩阵，以下公式w[i-1],p[i-1]代表从第一个元素w[0],p[0]开始取。
            if(j>=w[i-1]) and res[i-1][j-w[i-1]]+p[i-1]>res[i][j]:
                res[i][j]=res[i-1][j-w[i-1]]+p[i-1]
              #  print("i=%d;j=%d;p[i-1]=%d;res[i][j]=%d" %(i,j,p[i-1],res[i][j]))
    return res
#打印最大价值和要选择的商品
def show(n,c,w,res):
    print('最大价值为:',res[n][c])
    rr= res[n][c] - p[n - 1]
    print ("第%d个" %(n-1))
    flag = False
    while rr !=0:
        for i in range(1,n+1):
            for j in range(1,n+1):
                if res[i][j] == rr:
                    print("第%d个" %(i-1))
                    rr = res[i][j] -p[i-1]
                    flag = True
            if flag:
                flag = False
                break


if __name__=='__main__':
    #物品件数
    n=3
    #背包的最大承重
    c=4
    #各个物品的重量
    w=[4,3,1]
    #各个物品的价值
    p=[3000,2000,1500]
    res=bag(n,c,w,p)
    show(n,c,w,res)

动态规划算法的精髓在于合并两个子问题的解来得到更大问题的解。

假设发现还有第四件商品可偷一个iPhone！，怎么在原有的网格基础上拓展呢？步骤如下：
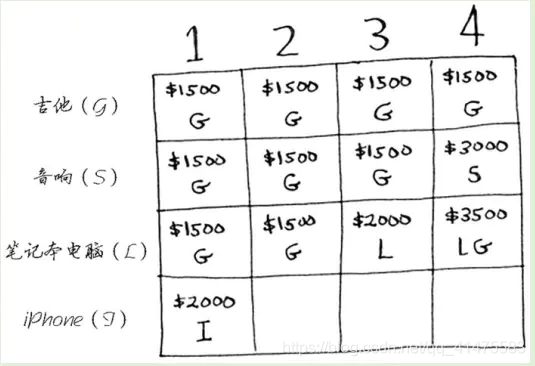
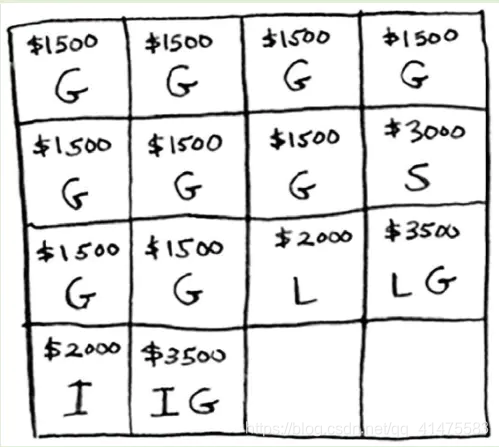
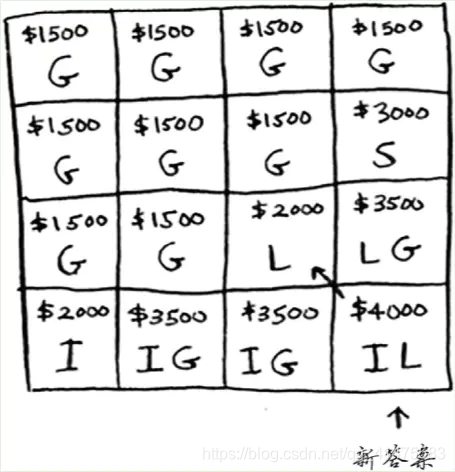
在这里插入图片描述

问题延申：

沿着列一直往下走，最大的价值有可能会下降吗？
答：不可能，每次迭代，都存储当前的最大值，最大值不可能比以前低。
假设还可以偷一条项链，重0.5磅，价值1000美元，此时网格该怎么调整？
答：需要考虑的粒度更细，需要调整网格，网格各列的重量相差为0.5磅。
可以偷一部分商品吗？如偷一点大米，这种情况下，不再是要么偷要么不偷，而是偷商品的一部分。可以使用动态算法计算吗？
答：不可以，使用动态规划时，要么考虑拿走整件商品，要么考虑不拿，没办法判断该不该拿走商品的一部分。此时可以使用贪婪算法解决这种情况。
计算最终的解时会涉及两个以上的子背包吗？
答：为获得背包问题的最优解，可能需要偷两件以上的商品。但根据动态规划算法的设计，最多只需合并两个子背包，即根本不会涉及两个以上的子背包。不过这些子背包可能又包含子背包。
最优解可能导致背包没装满吗？
答：完全有可能！

3、最长公共子串

绘制网格：

必须思考一下几个问题：

单元格中的值是什么？
如何将这个问题划分为子问题？
网格的坐标轴是什么？

填充网格

如果俩个字母不相同，则值为0
如果俩个字母相同，值为左上角数字加1

FISH与HISH的公共子串：

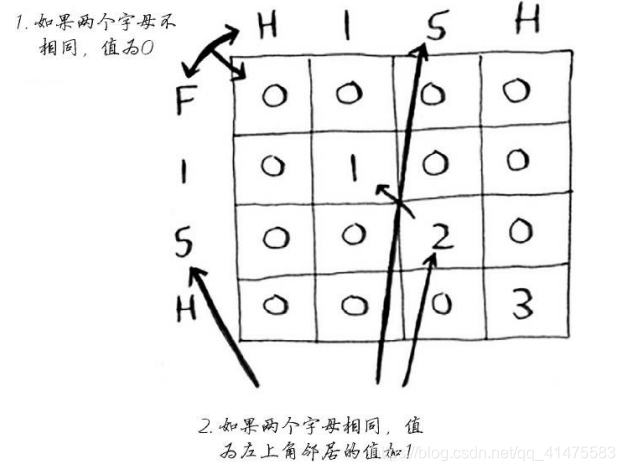
在这里插入图片描述
伪代码如下：

if word_a[i] == word_b[j]: 
	#两个字母相同
	cell[i][j] = cell[i-1][j-1] + 1
else: 
	#两个字母不同
	cell[i][j] = 0

注意： 这个问题的最终答案并不在最后一个单元格中！前面的背包问题，最终答案都在最后的单元格中，但对于最长公共子串问题，答案为网格中最大的数字，并不一定位于最后的单元格中。

最长公共子序列：

引入：
假设jason不小心输入了fosh，他原本想输入的是fish还是fort呢？
我们使用最长公共子串公式来比较它们。
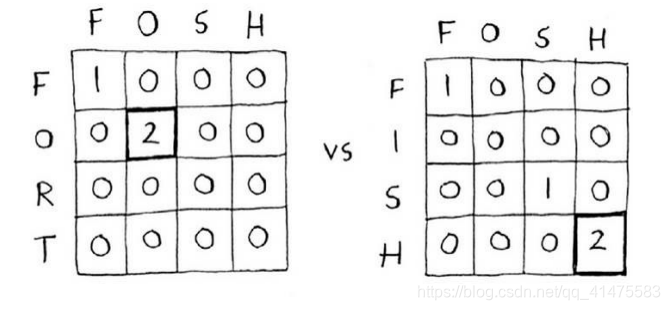
在这里插入图片描述
最长公共子串的长度相同，都包含两个字母！但显然fosh与fish更像！！！那此时怎么解决这个问题，就需用到最长公共子序列了。

网格展示：
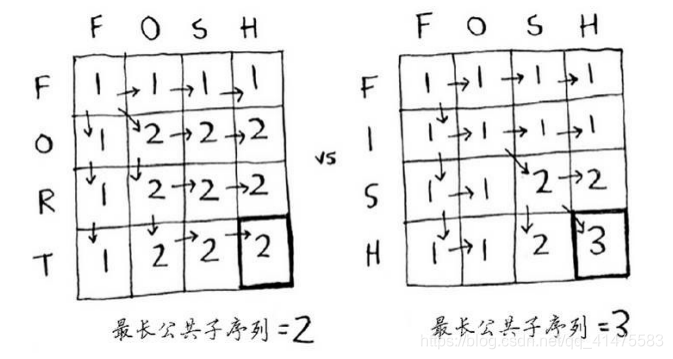
在这里插入图片描述

算法为：

如果俩个字母不相同，就选择左方或者上方较大的填入。
如果俩个字母相同，选择左上方的数字加1填入。

伪代码：

if word_a[i] == word_b[j]:
	#两个字母相同
	cell[i][j] = cell[i-1][j-1] + 1
else:
	#两个字母不相同
	cell[i][j] = max(cell[i-1][j], cell[i][j-1])

4、实际应用

生物学家根据最长公共序列来确定DNA链的相似性，进而判断两种生物或疾病有多相似。最长公共序列还被用来寻找多发性硬化症治疗方案。对生物信息感兴趣的，可以看看北京大学生物信息学课程。
git diff等命令，它们指出两个文件的差异，也是使用动态规划实现的。
字符串的相似程度。编辑距离指出两个字符串的相似程度。也是使用动态规划得到的。编辑距离算法的用途很多，从拼写检查到判断用户上传的资料是否为盗版，都在其中。
诸如Microsoft Word等具有断字功能的应用程序，它们如何确定在什么地方断字以确保行长一致，使用的是动态规划。