机器学习基石02：感知机（perceptron）与 PLA（Perceptron Learning Algorithm）

在开始学习机器学习的时候，没有注重算法是怎么推导的，也没有及时复习，导致现在论文中很多看不懂，遂决定重新学习机器学习的相关算法。相关博客以小白的视角和思路将自己的思考过程记录下来，一方面是对自己学习的记录，方便复习；另一方面，也希望能给入门的小伙伴提供参考。网上资源很丰富，但这也带来了选择困难，可能资料收藏下载了一大堆，开始学的时候全打开，又感觉无从下手，导致一直浮在面上，哪一门都没学好。其实，很多课程都是相通的，选择一门深入，按照课程的流程走下来，完成课程相关作业，并将算法自己推导一遍。实在是看不懂的也要标记出来，不要只是看视频，当时看懂了觉得会了就不管了，这样过几天就忘记了。记笔记的时候不要只做课本的搬运工，一定要内化，加入自己的思考，多少无所谓，只要自己想明白一个问题，就是有提高有收获了。一遍不会，多看几遍，毕竟我们都是奔着算法工程师去的，加油！本人水平有限，可能存在错误，欢迎各位指出，大家一起进步！

本文是在红色石头的林轩田机器学习基石笔记lecture2（github笔记链接）的基础上做了扩展。原来的笔记本身质量很高，但是不太适合我这样的小白，因此结合林轩田老师的课件和视频（b站有）还有其他的资源（主要是PRML）将课程和笔记中不易理解的地方作了补充。

感知机是 10种统计学习方法 的第一种，图片来自李航《统计学习方法》第2版课件。

2.Perceptron Algorithm

引用《PRML》中对感知器的介绍。

感知器算法是由Rosenblatt（1962）提出的线性判别模型。它在模式识别算法的历史中具有重要地位。它对应于⼀个⼆分类的模型，这个模型中，输⼊向量x⾸先使⽤⼀个固定的⾮线性变换得到⼀个特征向量 $ϕ(x)$，这个特征向量然后被⽤于构造⼀个⼀般的线性模型，形式为 $y(x) = f(w^T ϕ(x))$，其中非线性激活函数 $f(·)$是一个阶梯函数（跟下文 $sign$函数功能相同，只不过阶梯函数是模式识别中的叫法。）

2.1 Perceptron Hypothesis Set

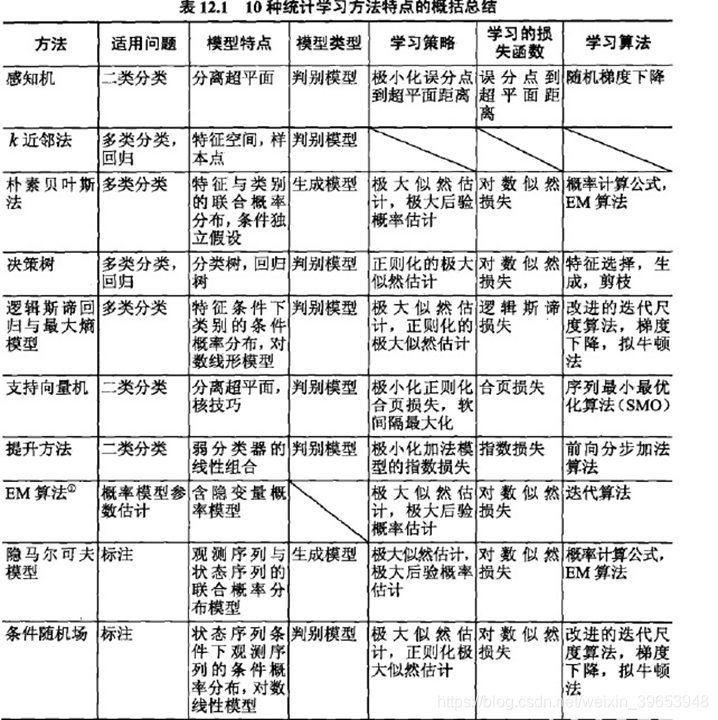
引入一个例子：某银行要根据用户的年龄、性别、年收入等情况判断是否给用户发信用卡。现有训练样本D，即之前用户信息和是否发了信用卡。这是一个典型的机器学习问题，我们要根据D，通过A，在H中选择最好的h，得到g，接近目标函数f，也就是根据先验知识建立是否给用户发信用卡的模型。银行用这个模型对以后用户进行判断：发信用卡（+1），不发信用卡（1）。

在这个流程中，有一部分非常重要：模型选择（Hypothesis Set）。选择什么样的模型，很大程度上会影响机器学习的效果和表现。一个简单常用的 Hypothesis Set 是 感知机（Perceptron）模型。

接上例，把用户的个人信息作为特征向量x，令总共有d个特征，每个特征赋予不同的权重w（也可理解为分割直线的法向量），表示该特征对输出（是否发信用卡）的影响有多大。那所有特征的加权和与一个设定的阈值threshold进行比较：大于阈值，输出为+1，即发信用卡；小于阈值，输出为-1，即不发信用卡。感知机模型，就是当 $特征加权和 - 阈值 ≥ 0$ 时，则输出 $h(x)=1$；当 $特征加权和 - 阈值 ＜0$ 时，则输出 $h(x)= -1$，算法就是要计算出所有 $权值w$和 $阈值threshold$。

推导过程如下：
构造hypothesis $h(x)$ ，（ $sign(x)，当x>0，sign(x)=1;当x=0，sign(x)=0; 当x<0， sign(x)=-1$），这样就可以用数学语言描述满足条件与否和发卡与否的关系。在这个模型中， $x_i$是样本数据， $w_i$ 和 $threshold$ 是算法需要学习的参数。为了方便表示，通常将 $threshold$ 当做 $w_0$，引入 $x_0 = 1$ 与 $w_0$ 相乘。进一步写成权重向量 $w$转置 $w^T$ 与样本 $x$ 相乘的形式，这样表示其实是点积运算，方便以后PLA修正分割直线。


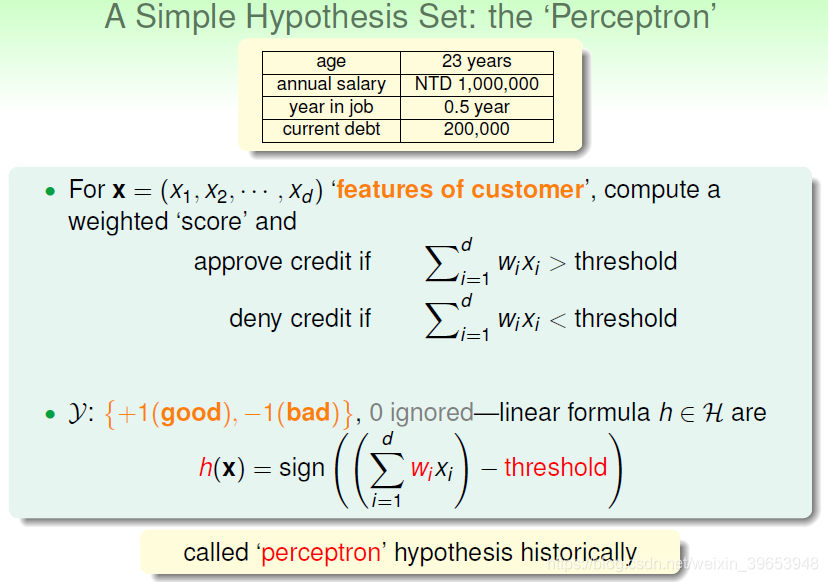
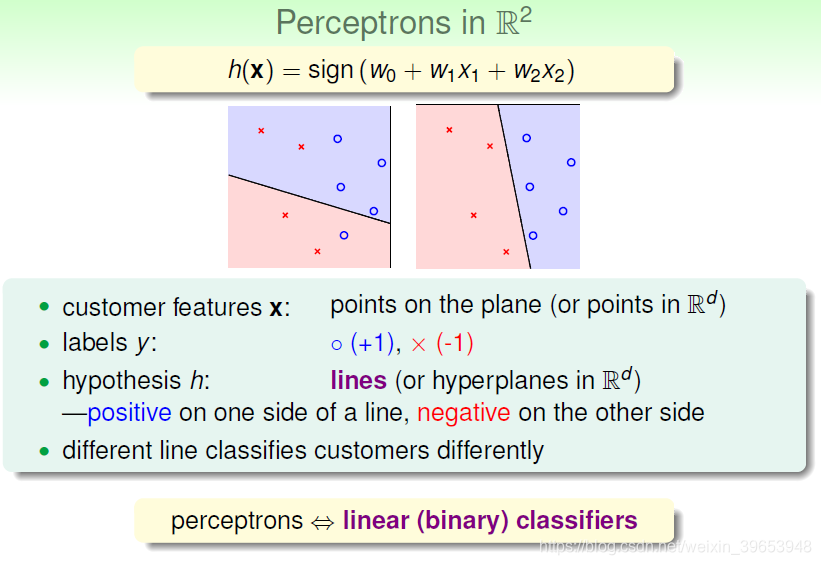
更为直观的说明，将用户数据映射到二维平面，其中蓝色○代表发信用卡，红色×代表不发。那么感知机模型的 h(x) 中的约束条件 $w_0 + w_1 x_1 + w_2 x_2$ 就是图中的一条分割直线，也就是 感知器（Perceptron），称之为 linear（binary） classifiers 。法向量方向一侧为正类（positive/+1/○），另一侧为负类（negative/-1/），权重 $w$不同，分割直线也不同。linear(binary) classifiers是用简单的感知器模型建立的，线性分类问题还可用logistic regression解决。

做个例题。

感知器收敛定理（perceptron convergence theorem）表明，如果存在⼀个精确的解（即，如果训练数据线性可分），那么感知器算法可以保证在有限步骤内找到⼀个精确解。但是，达到收敛状态所需的步骤数量可能⾮常⼤，并且在实际应⽤中，在达到收敛状态之前，不能够区分不可分问题与缓慢收敛问题。即使数据集是线性可分的，也可能有多个解，并且最终哪个解会被找到依赖于参数的初始化以及数据点出现的顺序。此外，对于线性不可分的数据集，感知器算法永远不会收敛。

2.2 Perceptron Learning Algorithm(PLA)

由上节知，hypothesis set 是许多分割直线的集合，那如何从中找到一条最优的直线，将平面中的两类完全分开，这就是PLA的目的。

PLA的思想是：“逐步修正”。首先，在平面上随取一直线，观察哪些点分类错误。然后针对第一个点开始修正分割直线的位置，使这个错误点变成分类正确的点。接着，再针对第二个、第三个等所有的错误分类修正分割直线，直到所有点都完全分类正确，就找到了最好的分割直线。如下图所示。

PLA做法：首先随机选择一条分割直线进行二分类，然后找到第一个分类错误点（ $x$），此时有两种情况。第一种情况，如果这个点表示正类，被误分为负类，即 $w^T_t x_n(t)<0$ ，表示 $w$和 $x$夹角＞90°（可以这么理解， $w^T_t x_n(t)$表示分割直线的法向量与起点到被错分类的点 $x$构成的向量的点积运算，当两向量点积结果<0时，表示两向量的夹角＞90°），其中 $w$是分割直线的法向量。所以， $x$被误分在直线的下侧（相对于法向量。法向量 $w$的方向即为正类所在的一侧），修正的方法就是使 $w$和 $x$夹角＜90°。通常做法是 $w ← w + yx, y = 1$（相当于两向量相加），如下图右上角所示，一次或多次更新后，更新后的分割直线的法向量 $w + yx$ 与 $x$夹角已经＜90°，此时可以保证x位于分割直线的上侧（即，分割直线法向量指向的一侧，为正例），对误分为负类的错误点 $x$完成了修正。

同理，如果是被误分为正例的点（本身是负例），即 $w^T_t x_n(t)＞0$ ，表示 $w$和 $x$夹角＜90°（可以这么理解， $w^T_t x_n(t)$表示分割直线的法向量与起点到被错分类的点 $x$构成的向量的点积运算，当两向量点积结果＞0时，表示两向量的夹角＜90°），其中 $w$是分割直线的法向量。所以， $x$被误分在直线的下侧（相对于法向量。法向量 $w$的方向即为正类所在的一侧），修正的方法就是使 $w$和 $x$夹角＜90°。通常做法是 $w ← w + yx, y = -1$（相当于两向量相加），如下图右下角所示，一次或多次更新后，更新后的分割直线的法向量 $w + yx$ 与 $x$夹角已经＞90°，此时可以保证x位于分割直线的下侧（即，分割直线法向量指向的反方向一侧，为负例），对误分为正类的错误点 $x$完成了修正。

算法运算过程中，可以遍历所有数据，直到所有点全部分类正确，要注意PLA直针对二分类线性可分的有效。

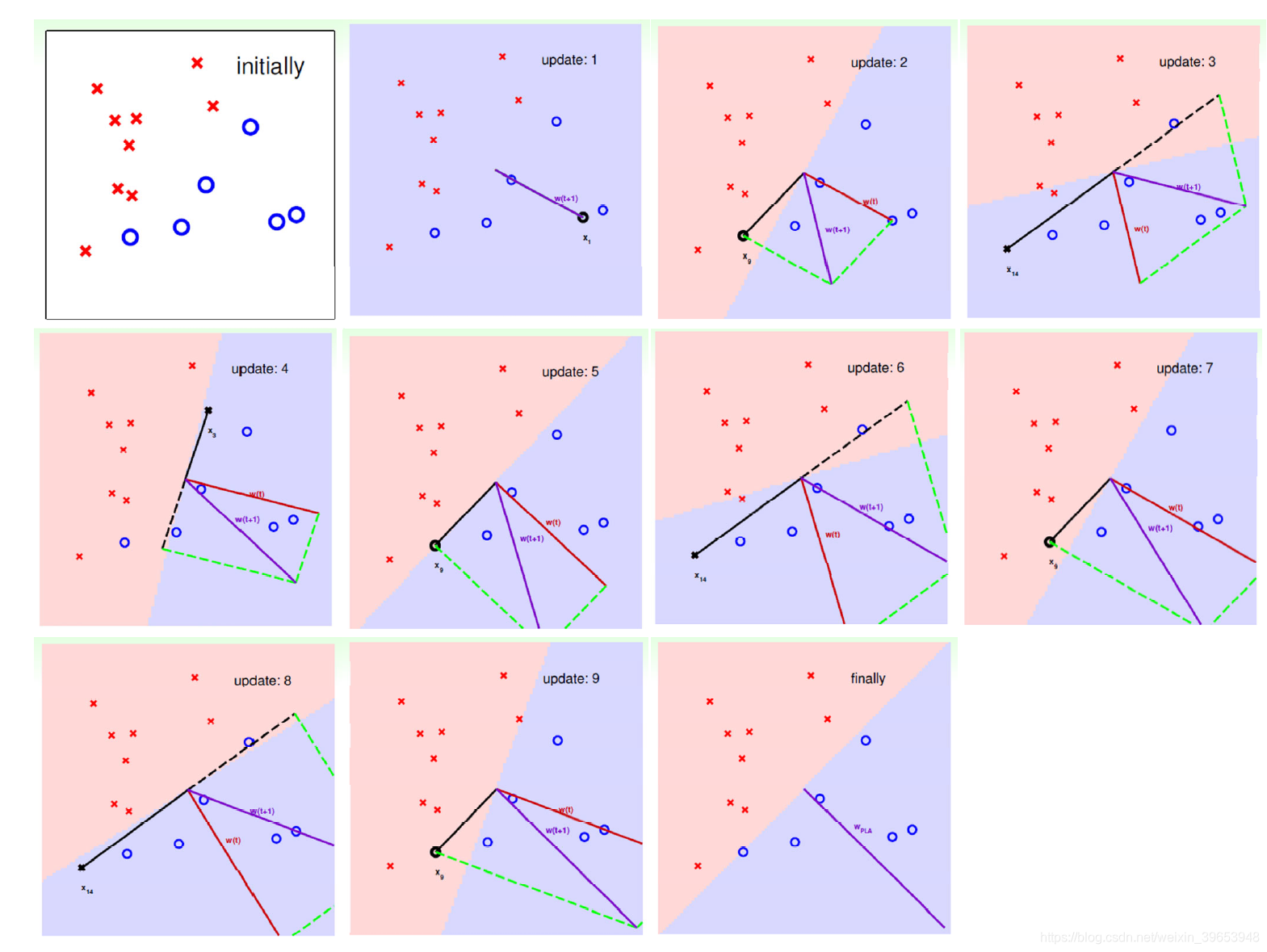
看下边的例子，红色线表示更新前的分割直线法向量 $w(t)$，紫色线表示下一步要更新的分割直线的法向量 $w(t+1)$，黑色线表示当前二分类情况下，被错分类的点的向量。比如在update2到update3的更新过程中，update2中黑色点 $x9$是正例（○），被错分为负例（×），即 $w^T_t x_n(t)<0$ ，表示 $w$和 $x$夹角＞90°，按照上面介绍的向量更新规则，修正的方法就是使 $w$和 $x$夹角＜90°，通常做法是 $w ← w + yx, y = 1$，使得点 $x9$位于分割直线的法向量方向区域（正例区域），图中为紫色区域。更新之后到update3。以此类推，直到找到分割直线将数据完全分开，此时的hypothesis set $h(x)$即为最优的。

例题。

2.3 Guarantee of PLA

对于线性可分的二分类问题，PLA什么时候停下呢？

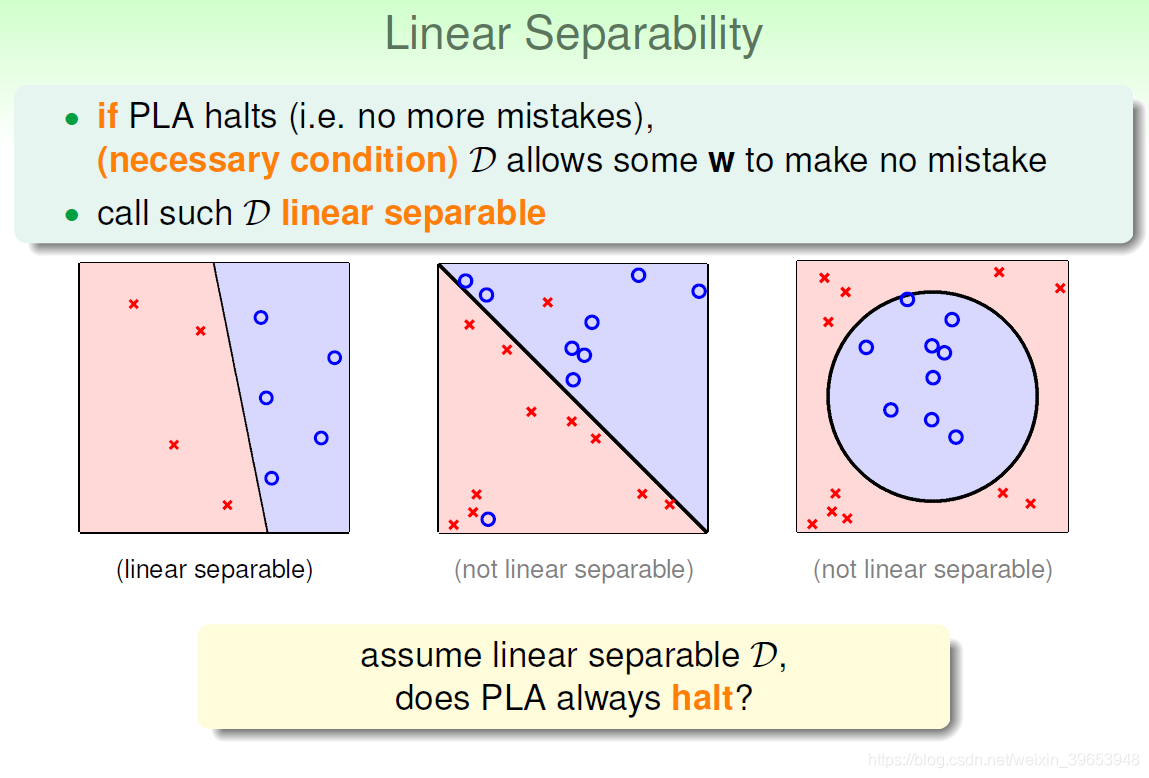
看具体的过程，我们假设存在最优（目标）的分割直线法向量 $w^T_f$，更新后的分割直线的法向量为 $w_{t+1}$，之所以将 $w^T_f·w_{t+1}$作为评价是否最优的标准，可以这么理解，还是两向量点积的问题，向量长度（模长）不变的情况下，两向量点积越大（>0）表示两向量夹角越小，即 $w_{t+1}$越来越接近 $w^T_f$，表示PLA学习是有效的；小到0度的时候，两向量同向共线，此时的 $w_{t+1}$即为最优的分割直线的法向量 $w^T_f$。但是不要忘记，我们假设了两向量模长不变，考虑实际情况，两向量点击增大，还有可能是模长增大引起的，所以还要证明向量 $w_{t+1}$和 $w_t$的长度关系。

对于 $y_n(t) w^T_f x_n(t) >0$可以这么理解： $y_n(t)$的取值要么是1，要么是-1。由上文的分析可知，当正例被错分为负例的时候，两向量的点积 $w^T_f x_n(t) ＜0$，再乘以-1（ $y_n(t)$）， 结果＞0；当负例被错分为正例的时候，两向量的点积 $w^T_f x_n(t) >0$，再乘以1（ $y_n(t)$），结果＜0，所以可证 $y_n(t) w^T_f x_n(t) ≥ miny_n w^T_f x_n >0$，接着不难证明 $w^T_f w_{t+1} >0$。


$w_t$只会在分类错误的情况下更新，最终得到的 $||w_{t+1}||^2$相比 $||w_t||^2$的增量值不超过 $max||x_n||^2$。也就是说， $w_t$的增长被限制了， $w_{t+1}$与向量 $w_t$长度不会差别太大！
如果令初始权值，那么经过T次错误修正后，有如下结论：

下面是该结论的具体推导过程：

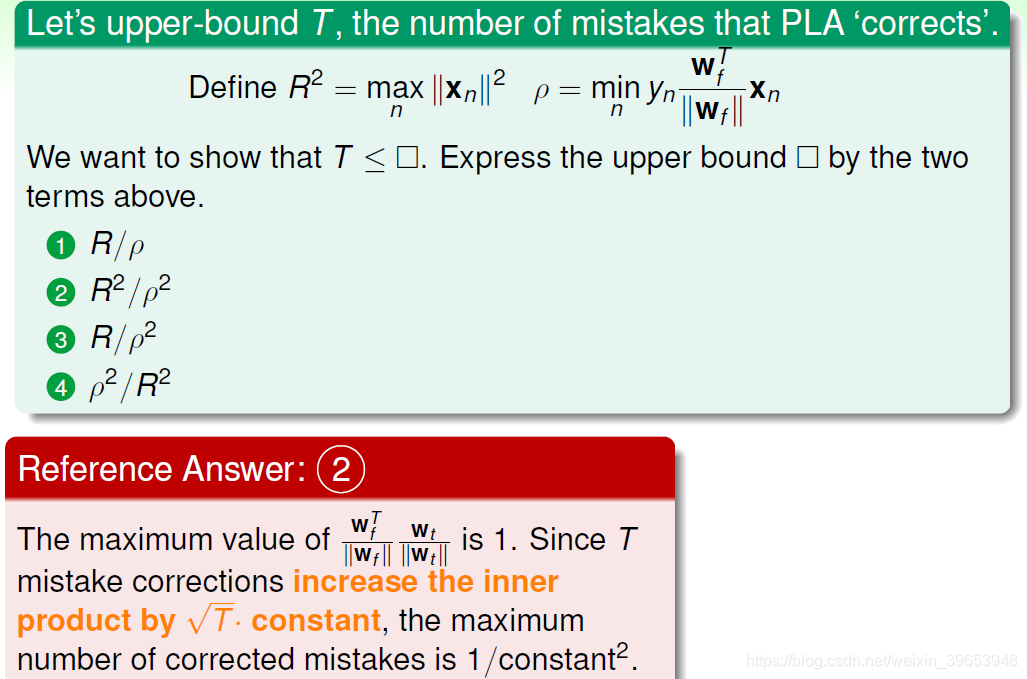
上述不等式左边其实是 $w^T_f$与 $w_f$夹角的余弦值，随着T增大，该余弦值越来越接近1， 即 $w^T_f$与 $w_f$越来越接近。同时，需要注意的是， $\sqrt[2]{T}·constant ≤1$ ，也就是说， 迭代次数 $T$是有上界的。根据以上证明，我们最终得到的结论是： $w_{t+1}$与 $w_f$的是随着迭代次数增加，逐渐接近的。而且，PLA最终会停下来（因为 $T$有上界），实现对线性可分的数据集完全分类。

例题

2.4 NonSeparable Data

对于费线性可分的情况， $w_f$实际上并不存在，之前的推导并不成立，PLA也不一定会停下来。

对于非线性可分的情况，可以把它当成是数据集D中掺杂了一下noise，事实上， 大多数情况下的D，都或多或少地掺杂了noise。这时，机器学习流程是这样的：

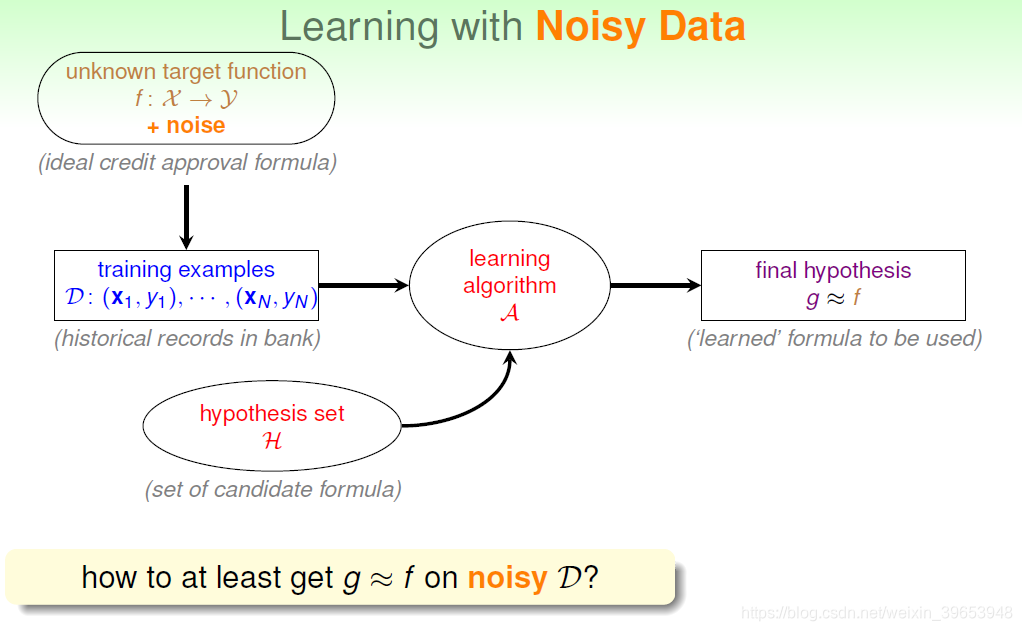
在非线性情况下，可以把条件放松，即不苛求每个点都分类正确，而是容忍有错 误点，取错误点的个数最少时的权重 $w$：

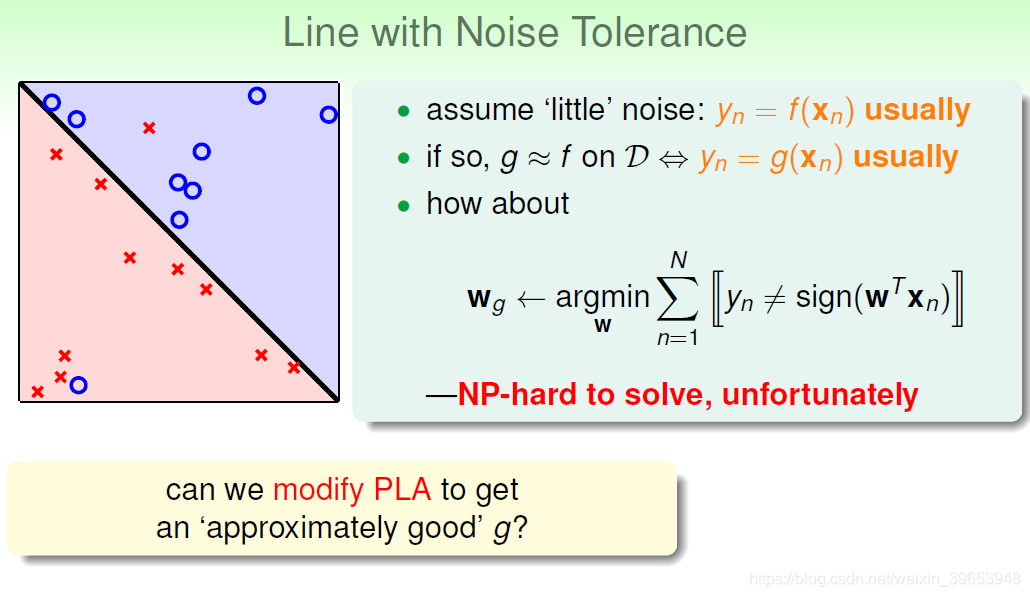
事实证明，上面的解是NPhard 问题，难以求解。然而，可以对在线性可分类型中表现很好的PLA做个修改，把它应用到非线性可分类型中，获得近似最好的 $g$。

修改后的PLA称为Packet Algorithm。它的算法流程与PLA基本类似，首先初始化权 $w_0$ ，计算出在这条初始化的直线中，分类错误点的个数。然后对错误点进行修正，更新 $w$，得到一条新的直线，再计算其对应的分类错误的点的个数，并与之前错误点个数比较，取个数较小的直线作为我们当前选择的分类直线。之后，再经n次迭代，不断比较当前分类错误点个数与之前最少的错误点个数比较，选择最小的值保存。直到迭代次数完成后，选个数最少的直线对应的 $w$，即为最终想要的权重。

如何判断数据集D是不是线性可分？对于二维数据来说，通常还是通过肉眼观察判断。一般情况下，Pocket Algorithm要比PLA速度慢。

Summary

本节课主要介绍了线性感知机模型，以及解决这类感知机分类问题的简单算法： PLA。详细证明了对于线性可分问题，PLA可以停下来并实现完全正确分类。对于不是线性可分的问题，可以使用PLA的修正算法Pocket Algorithm来解决。