中国剩余定理
设m1,m2...,mn是两两互质的整数,m=∏ni=1mi,Mi=m/mi,ti是线性同余方程Mi*ti≡1(mod mi)的一个解。对于任意的n个整数a1,a2,...,an
,方程组
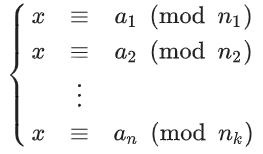
有整数解,解为x=∑aiMiti。
算法流程

证明过程

应用
某些计数问题或数论问题出于加长代码、增加难度、或者是一些其他不可告人的原因,给出的模数: 不是质数 !
但是对其质因数分解会发现它没有平方因子,也就是该模数是由一些不重复的质数相乘得到。
那么我们可以分别对这些模数进行计算,最后用 CRT 合并答案。
求解方法

#include<iostream> #include<vector> #include<algorithm> #include<queue> #include<cstring> #include<cstdio> using namespace std; typedef long long lt; lt read() { lt f=1,x=0; char ss=getchar(); while(ss<'0'||ss>'9'){if(ss=='-')f=-1;ss=getchar();} while(ss>='0'&&ss<='9'){x=x*10+ss-'0';ss=getchar();} return f*x; } const int maxn=100010; int n; lt ai[maxn],bi[maxn]; lt mul(lt a,lt b,lt mod) { lt res=0; while(b>0) { if(b&1) res=(res+a)%mod; a=(a+a)%mod; b>>=1; } return res; } lt exgcd(lt a,lt b,lt &x,lt &y) { if(b==0){x=1;y=0;return a;} lt gcd=exgcd(b,a%b,x,y); lt tp=x; x=y; y=tp-a/b*y; return gcd; } lt excrt() { lt x,y,k; lt M=bi[1],ans=ai[1];//第一个方程的解特判 for(int i=2;i<=n;i++) { lt a=M,b=bi[i],c=(ai[i]-ans%b+b)%b;//ax≡c(mod b) lt gcd=exgcd(a,b,x,y),bg=b/gcd; if(c%gcd!=0) return -1; //判断是否无解,然而这题其实不用 x=mul(x,c/gcd,bg); ans+=x*M;//更新前k个方程组的答案 M*=bg;//M为前k个m的lcm ans=(ans%M+M)%M; } return (ans%M+M)%M; } int main() { n=read(); for(int i=1;i<=n;++i) bi[i]=read(),ai[i]=read(); printf("%lld",excrt()); return 0; }
bi对应ni,ai就是ai