数论中国剩余定理（非拓展）基础

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/w_udixixi/article/details/100898366

中国剩余定理

（一）定理描述

$给出一组同余方程组（S） \begin{cases} x\equiv a_1(mod \ m_1)\\ x\equiv a_2(mod \ m_2)\\ x\equiv a_3(mod \ m_3)\\ ..\\ ..\\ x\equiv a_n(mod \ m_n)\\ \end{cases}$
当正整数 $m_1,m_2……m_n$两两互质时，对于任意的整数 $a_i(1\leq i \leq n)$, $S$有解

$x$的通解可以如下表示：
$设(1\leq i\leq n)$
$M=\prod_{i=1}^nm_i$

$M_i={M\over {m_i}}$

$t_i为M_i在模m_i意义下的逆元,即M_i^{-1}$

则 $x=kM+\sum_{i=1}^na_it_iM_i,k\in Z$

特别的，在模M意义下，S仅有唯一解 $x=\sum_{i=1}^na_it_iM_i$

---

（二）例子解释

假设现在给出三个两两互质的数3，5，7,求满足方程组的 $x$
即
$\begin{cases} x\equiv 2(mod \ 3)\\ x\equiv 3(mod \ 5)\\ x\equiv 2(mod \ 7)\\ \end{cases}$

公式的证明暂时先不深究。
通过这个例子来理解一下：
$M=m_1m_2m_3=105$;
$M_1=35=5*7,M_2=21=3*7,M_3=15=3*5$;
按照公式的意思,求出 $t_1=M_1^{-1}=2,t_2=M_2^{-1}=1,t_3=M_3^{-1}=1$
$t_1M_1=70,t_2M_2=21,t_3M_3=15$

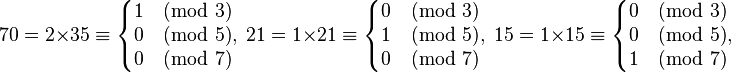
这里也涉及到逆元的定义：如果 $gcd(a,p)=1,且ax\equiv 1(mod \ p)$,则称x是a模p意义下的逆元
由于 $m_i$两两互质（即没有公共质因子）这个特点，可以口胡出为什么一定会出现上述的规律，即 $a_it_iM_i$对原来n个模数的模有一个1和n-1个0

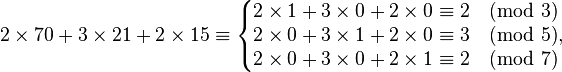
那么一个 $x=233$就这样被找到了，那么x的通解怎么找呢？

设解系 $X=233+kH,k\in Z$,这个H有什么特点呢,由于加上这个H对 $3,5,7$取模并没有影响，即仍符合方程组，说明 $H\%3=0,H\%5=0,H\%7=0$，又因为 $m_i$两两互质的原因，所以H=3×5×7=105，即之前定义的M

---

（三）代码

ll Chinese_solve(ll a[],ll Mod[],int n)
{
    ll res=0;
    ll M=1;
    repp(i,0,n)M*=Mod[i];
    repp(i,0,n)
    {
        ll m_i=M/Mod[i];
        ll gcd=exgcd(m_i,Mod[i],x,y);
        res=(res+x*a[i]*m_i)%M;
    }
    return (M+res%M)%M;
}

---

例题：POJ1006 模板题

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<bitset>
#include<cstdlib>
#include<cmath>
#include<set>
#include<list>
#include<deque>
#include<queue>
#include<map>
#define ll long long
#define pb push_back
#define rep(x,a,b) for (int x=a;x<=b;x++)
#define repp(x,a,b) for (int x=a;x<b;x++)
#define W(x) printf("%d\n",x)
#define WW(x) printf("%lld\n",x)
#define pi 3.14159265358979323846
#define mem(a,x) memset(a,x,sizeof a)
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
using namespace std;
const int maxn=2e6+7;
const int INF=1e9;
const ll INFF=1e18;
ll a[maxn];
ll Mod[maxn];
int n;
ll x,y,d;
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if (b==0)
    {
        x=1;
        y=0;
        return a;
    }
    ll g=exgcd(b,a%b,y,x);
    y-=(a/b)*x;
    return g;
}

ll solve(ll a[],ll Mod[],int n)
{
    ll res=0;
    ll M=1;
    repp(i,0,n)M*=Mod[i];
    repp(i,0,n)
    {
        ll m_i=M/Mod[i];
        ll gcd=exgcd(m_i,Mod[i],x,y);
        res=(res+x*a[i]*m_i)%M;
    }
    ll x=(M+res%M)%M;
    while(x-M>=d){x-=M;}
    while(x<=d){x+=M;}
    return x;
}
int main()
{
    int K=0;
    while(~scanf("%lld%lld%lld%lld",&a[0],&a[1],&a[2],&d)&&a[0]+a[1]+a[2]+d!=-4)
    {
        Mod[0]=23;
        Mod[1]=28;
        Mod[2]=33;
        ll ans=(solve(a,Mod,3)-d);
        printf("Case %d: the next triple peak occurs in %lld days.\n",++K,ans);
    }
}