Lecture2:Markov Decision Process

Markov Process

几乎所以的强化学习问题都可以表述成马尔可夫决策过程（MDP）的形式。

Markov Property

Definition
A state $S_t$ is Markov if and only if
$\mathbb{P}[S_{t+1}|S_t]=\mathbb{P}[S_{t+1}|S_1,\dots,S_t]$
下一个状态只与当前状态有关

从状态s到状态s’的状态转移概率
$P_{ss'}= \mathbb{P}[S_{t+1}=s'|S_t=s]$
状态转移矩阵定义从状态s到状态s’的转移概率。

Markov Process

马尔可夫过程中的所有状态均满足马尔可夫性，马尔可夫过程可以表示成一个而元组，包含状态和状态转移矩阵。

下图是一个马尔可夫过程的例子。初始状态为C1，最终状态为Sleep。

采样（sample）是一个非常重要的概念。如图所示，采样的初始状态为C1，最终状态为Sleep。
比如：

• C1 C2 C3 Pass Sleep
• C1 FB FB C1 C2 Sleep
• C1 C2 C3 Pub C2 C3 Pass Sleep
  采样的长度是不固定的是随机的。
  
  马尔可夫过程可以用上述状态转移矩阵表示，第一行第二列是0.5，也就是从C1到C2的转移概率，第二行，第三列为0.8，也就是从C2到C3的转移概率。每一行的总和为1。

Markov Reward Process

可以认为带有value的马尔可夫过程。

R告诉我们从在时间t，状态s的时候，能获得多少reward，这是立即奖励，也就是t+1时候的reward。

Return

$G_t$可以看作是从时间t开始到结束的累计奖励。
$\gamma \in [0,1]$
当 $\gamma$接近于0时，我们倾向于短期的reward，当接近于1时，倾向于长期reward。

为什么要设置衰减因子 $\gamma$？

Value Function

value function 衡量在状态s时，到结束时可以获得reward的总和，也就是对 $G_t$的期望。

还是以上面的为例子：从C1开始， $\gamma = \frac{1}{2}$
$G_1 = R_2 + \gamma R_3 + \dots +\gamma^{T-2}R_T$

可以理解为 $G_1$是一个随机变量， $G_1$是 $R_2,R_3,\dots$这些随机变量的和，v是 $G_1$的期望。

Bellman Equation

当前的value function可以看出两部分组成。它的基本思想就是递归分解。

对于MRP而言，奖励仅仅与状态有关，因此bellman方程可以做一下分解表示：

在bellman方程中，值函数被分解为两部分，一部分是对于t+1时间步的奖励的期望，另一部分是对于有折扣的下一状态值的期望。第一部分中由于t+1步的奖励就是t时刻的状态所获得的奖励，因此期望可以直接略去；第二部分则是利用状态转移矩阵对状态值函数求的期望。

bellman equantion的矩阵表示形式

这里前面的v和后面的v是相同的，就是待求解矩阵。这种方法只适合状态比较少的情况。

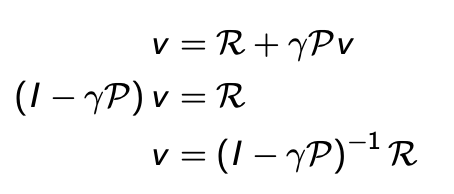
Markov decision Process

MDP是一个包含MRP的决策过程。它是一个所有状态都具有马尔可夫性的环境。

Policy

A policy $\pi$ is a distribution over actions given state,
$\pi(a|s) = \mathbb{P}[A_t = a | S_t = s]$

这里的policy $\pi$ 中并不包含reward，因为我们并不关心过去所得的reward，我们的策略是最大化将来的reward。此外，当前的state包含之前的所有信息。

• Policy 完全定义了agent的行为
• MDP policy 只依赖于当前的状态
• Policy是固定的，与时间无关
  $A_t \sim \pi(\cdot | S_t ), \forall t>0$
• 给定一个 MDP $M = <S,A,P,R,\gamma>$和policy $\pi$，状态序列 $S_1,S_2,\dots$ 是markov过程 $<S,P^{\pi}>$, 状态和奖励序列 $S_1,R_1,S_2,\dots$也是markov过程 $<S,P^{\pi},R^{\pi},\gamma>$
• 其中：
  $P_{s,s'}^{\pi}=\sum_{a\in A} \pi(a|s)P_{ss'}^{a}$
  $R_{s}^{\pi}=\sum_{a\in A} \pi(a|s)R_{s}^{a}$

Value Function

之前提到的是不包含action的value function，也就是上图中的state-value function，他是关于state 的value function。这里又补充了关于action的value function。 $v_{\pi}(s)$可以理解为状态s有多好， $q_{\pi}(s,a)$可以理解为在状态s下采取action a有多好。

Bellman Expectation Equation

之前提到的关于state的bellman equation为：
$v_{\pi}(s) = \mathbb{E}_{\pi}[R_{t+1} + \gamma v_{\pi}(S_{t+1})|S_t = s ]$
现在关于action的bellman equation为：
$q_{\pi}(s,a) = \mathbb{E}_{\pi}[R_{t+1} + \gamma q_{\pi}(S_{t+1},A_{t+1})|S_t=s,A_t = a ]$
下面用树状图解释一下：
白色的圈为状态，黑色的点为action。

求根结点s的value $v_{\pi}(s)$，在状态s时，可能会以不同的概率 $\pi(a|s)$采取对应action，对应图中的两个黑色的点。采取每个action都会得到一个action-value function $q_{\pi}(s,a)$。这里把不同的action对应的值进行平均就得到了状态s时的value $v_{\pi}(s)$。

这幅树状图描述了在状态s时采取action a得到的 $q_{\pi}(s,a)$。每执行一次cation都会得到立即的reward $R_S^a$，然后会以概率 $P_{ss'}^a$转移到不同的状态s’。在不同的状态s’都会有 $v_{\pi}(s‘)$，这里对所有可能的状态s’进行平均，然后乘衰减因子 $\gamma$，再加上之前立即reward $R_S^a$ 就得到了最终的 $q_{\pi}(s,a)$。

下面两幅图是上面两幅图的组合。就是进行递归操作。



这里讲解一下7.4 是如何计算的。7.4是在状态C3是的value。在状态C3时，可能采取两种action分别为Study和Pub，对应的概率均为0.5，采取action Pub之后会得到立即奖励 +1，然后分别以0.2，0.4，0.4的概率转换为状态C1，C2，C3。采取action Study之后会得到立即奖励+10，然后以1.0的概率转移到结束状态。
7.4 = 0.5*(1+0.2*(-1.3)+0.42.7+0.47.4) + 0.5*(10+1*0)

Bellman Expectation Equation（Matrix Form）

$v_{\pi}=R^{\pi}+\gamma P^{\pi}v_{\pi}$
直接求解可得
$v_{\pi} = (1-\gamma P^{\pi})^{-1}R_{\pi}$

Optimal Value function

其实我们并不关心在markov chain中可以得到多少reward，我们关心的是在系统中找到最佳路径。

$v_*(s)$仅仅告诉了我们最大可能的reward，但是并没有告诉我们最好的policy是什么。
$q_*(s,a)$告诉了我们在状态s，采取a所获取的最大reward ，如果我们可以获取到 $q_*(s,a)$，我们就可以说MDP得到了解决。因此解决MDP可以认为是寻找 $q^*$。

Optimal Policy

如何定义好的Policy?
$\pi \geqslant \pi' \text{if} \ v_{\pi}(s) \geqslant v_{\pi'}(s),\forall s$

• 寻找optimal policy
  

Bellman Optimality Equation

在之前求 $v_{\pi}(s)$是平均不同action的reward $q_{\pi}(s,a)$，这里求 $v_{*}(s)$是找到最大的action所获得的reward $q_{*}(s,a)$。

这里求 $q_{*}(s,a)$和之前的操作相同，也是采取的平均的方法。
下面两幅图为上面的组合，采用了递归的方法。

这里是max（… + …）而不是max（…） + …

Bellman最优方程是非线性的，没有固定的解决方案,解决Bellman optimality equation 的方法通常是采样迭代的方法，比如

• Value Iteration
• Policy Iteration
• Q-learnig
• Sarsa

Extensions to MDPs

视频中简要提及，没有详细讲解。