马尔科夫过程(Markov Process,MP):
我们说一个state若满足 ,则其具有马尔可夫性,即该state完全包含了历史中的所有信息。马尔科夫过程是无记忆的随机过程,即随机状态序列 具有马尔可夫属性。
一个马尔科夫过程可以由一个元组组成\(\langle\mathcal{S}, \mathcal{P}\rangle\)
\(\mathcal{S}\)为(有限)的状态(state)集;
\(\mathcal{P}\)为状态转移矩阵, \[
P_{s s^{\prime}}=\mathbb{P}\left(S_{t+1}=s^{\prime} \mid S_{t}=s\right)
\] 。所谓状态转移矩阵就是描述了一个状态到另一个状态发生的概率,所以矩阵每一行元素之和为1。
马尔科夫决策过程(Markov Decision Process,MDP)
MDP相对于MP加入了瞬时奖励 \(R\)(Immediate reward)、动作集合\(A\)和折扣因子 \(\gamma\) (Discount factor),这里的瞬时奖励说的是从一个状态 s到下一个状态 s' 即可获得的rewards,虽然是“奖励”,但如果这个状态的变化对实现目标不利,就是一个负值,变成了“惩罚”,所以reward就是我们告诉agent什么是我们想要得到的,但不是我们如何去得到。
MDP由元组 \(\langle\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma\rangle\) 定义。其中
\(\mathcal{S}\)为(有限)的状态(state)集;
\(\mathcal{A}\)为有限的动作集;
\(\mathcal{P}\)为状态转移矩阵。所谓状态转移矩阵就是描述了一个状态到另一个状态发生的概率,所以矩阵每一行元素之和为1。[公式]
\(\mathcal{R}\)为回报函数(reward function), [公式]
\(\gamma\)为折扣因子,范围在[0,1]之间, 越大,说明agent看得越“远”。
对于每一个\(\pi\),\(a\in A\)
\[
\begin{aligned}
\mathcal{P}_{s, s^{\prime}}^{\pi} &=\sum_{a \in \mathcal{A}} \pi(a \mid s) \mathcal{P}_{s s^{\prime}}^{a} \\
\mathcal{R}_{s}^{\pi} &=\sum_{a \in \mathcal{A}} \pi(a \mid s) \mathcal{R}_{s}^{a}
\end{aligned}
\]
值函数和动作值函数
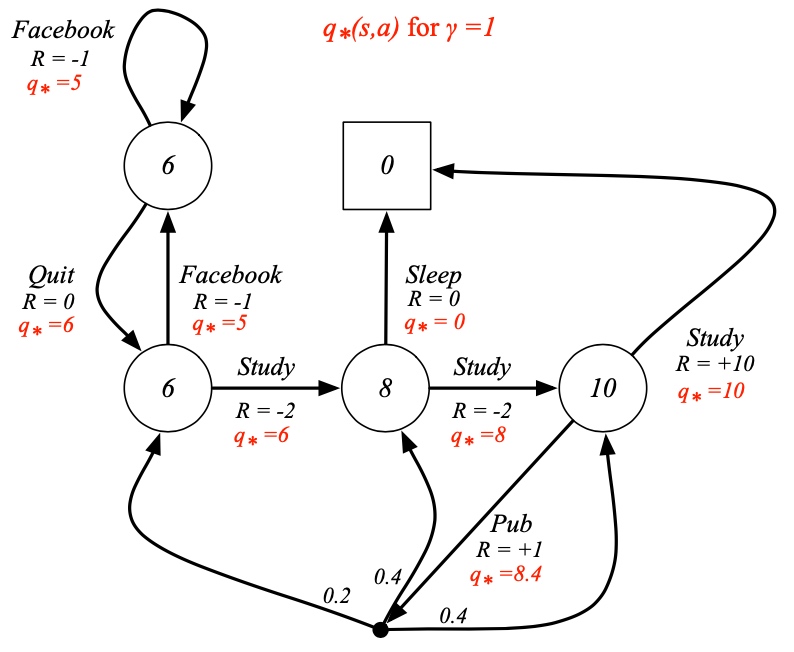
G值,从t时刻起,包括了未来,计算了折扣的总奖励:
\[
G_{t}=R_{t+1}+\gamma R_{t+2}+\ldots=\sum_{k=0}^{\infty} \gamma^{k} R_{t+k+1}
\]
值函数:在状态s,策略π下的值函数
\[
v_{\pi}(s)=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=s\right]
\]
动作值函数(action-value function):在状态s,执行动作a,遵循策略π,回报期望
\[
q_{\pi}(s, a)=\mathbb{E}_{\pi}\left[G_{t} \mid S_{t}=t, A_{t}=a\right]
\]
贝尔曼方程
状态值函数可以分解为即刻回报+未来回报x折扣值
分解 -> 迭代实现
\[
v_{\pi}(s)=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma v_{\pi}\left(S_{t+1}\right) \mid S_{t}=s\right]
\]
动作值函数类似:
\[
q_{\pi}(s, a)=\mathbb{E}_{\pi}\left[R_{t+1}+\gamma q_{\pi}\left(S_{t+1}, A_{t+1}\right) \mid S_{t}=s, A_{t}=a\right]
\]
在每个状态,会存在多个备选动作;
每个动作,也可能会导致不一样的状态,因此存在下图。
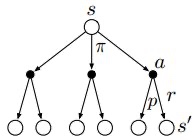
\[
v_{\pi}(s)=\sum_{a \in \mathcal{A}} \pi(a \mid s) q_{\pi}(s, a) \\ q_{\pi}(s, a)=\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{\pi}\left(s^{\prime}\right) \\
\]
于是
\[v_{\pi}(s)=\sum_{a \in \mathcal{A}} \pi(a \mid s)\left(\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{\pi}\left(s^{\prime}\right)\right) \\ q_{\pi}(s, a)=\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} \sum_{a^{\prime} \in \mathcal{A}} \pi\left(a^{\prime} \mid s^{\prime}\right) q_{\pi}\left(s^{\prime}, a^{\prime}\right)
\]
描述了当前状态值函数和其后续状态值函数之间的关系,即状态值函数(动作值函数)等于瞬时回报的期望加上下一状态的(折扣)状态值函数(动作值函数)的期望。
状态在策略下的value值,可以由一下的公式计算得到
\[
\begin{array}{c}
v_{\pi}=\mathcal{R}^{\pi}+\gamma \mathcal{P}^{\pi} v_{\pi} \\
v_{\pi}=\left(I-\gamma \mathcal{P}^{\pi}\right)^{-1} \mathcal{R}^{\pi}
\end{array}
\]
贝尔曼最优方程
学习的目的是优化一个策略π使得值函数v or q最大
\[
v_{*}(s)=\max _{\pi} v_{\pi}(s) \]
\[
q_{*}(s, a)=\max _{\pi} q_{\pi}(s, a) \]
对于任意一个MDPs,存在一个\(\pi_*\)使得\( v_{\pi_{*}}(s)=v_{*}(s), \quad q_{\pi_{*}}(s, a)=q_{*}(s, a) \)
可得,贝尔曼最优方程:
\[ v_{*}(s)=\max _{a} \mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} v_{*}\left(s^{\prime}\right) \]
\[ q_{*}(s, a)=\mathcal{R}_{s}^{a}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}}^{a} \max _{a^{\prime}} q_{*}\left(s^{\prime}, a^{\prime}\right)
\]