算法设计与分析课程复习笔记3——线性时间的排序法

线性时间的排序法

排序法回顾
插入排序：
易于实现，适合小规模输入（一般小于50个元素），对近似排序好的输入效果好
最坏情况：O（n²）

合并排序：
分治：分割、递归处理、线性时间合并
最坏情况：O（nlgn）

上述算法的共同点：基于元素之间的两两比较
通过比较获得输入元素之间的相对顺序，比较操作有：
$a_i$ < $a_j$ , $a_i$ ≤ $a_j$ , $a_i$ = $a_j$ , $a_i$ ≥ $a_j$ , or $a_i$ > $a_j$
(在最坏情况,基于比较思想的排序必须要做Ω(nlgn)次比较)

决策树模型（Decision Tree Model）

表示基于比较排序算法的所有可能比较情况
忽略了其他操作,比如控制,数据转移等操作
只考虑比较
三个基本元素

n!种排列对应同数目的叶节点
example：123，132，213，231，312，321共六种排列
决策树模型中必须出现与之对应的6个叶节点

最坏情况：从根到叶最长的路径
引理：任何树高为h的二分树最多有2^h个叶节点

任何基于比较的排序算法：n!≤叶节点数目≤2^h
h≥lg(n!)=Ω(nlgn)

计数排序

将要排序的元素是0到k之间的整数
对于每一个元素x，判断小于或等于元素x的元素的个数
根据计数的情况将元素放入到相应的位置

算法如下：
数组A是输入，数组B用于存放排序的输出，数组C提供临时存储空间

CountingSort(A,B,k)
	让C[0……k]成为一个新数组
	for i=0 to k                                   Θ(k)
		C[i]=0
	for j=1 to A.length                            Θ(n)
		C[A[j]]=C[A[j]]+1
	//C[i]现在存储了等于i的元素数目
	for i=1 to k                                   Θ(k)
		C[i]=C[i]+C[i-1]
	//C[i]现在存储了小于等于i的元素数目
	for j=A.length downto i                        Θ(n)
	//不从i到A.length而选择从A.length到i,这样保证了稳定性
	//即相等的输入元素的位置先后顺序在排列后输出的先后顺序不会改变.
		B[C[A[j]]]=A[j] //根据计数的情况将元素放到相应的位置
		C[A[j]]=C[A[j]]-1 //取出后减1

相等的输入元素的位置先后顺序在排列后输出的先后顺序不会改变：
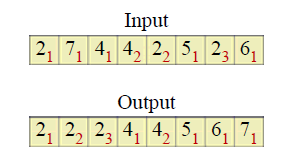
stable
时间开销：Θ（n+k）

基数排序

扩大了可排序的整数范围
数的基表示：
example:
16536 = 1 ⋅ 10⁴ + 6 ⋅ 10³ + 5 ⋅ 10² + 3 ⋅ 10¹ + 6 ⋅10^0
$(101101)_2$ = 1 ⋅ 2⁵ + 0 ⋅ 2⁴ + 1 ⋅ 2³ + 1 ⋅ 2² + 0 ⋅2¹+ 1 ⋅ 2⁰=45

算法如下：从最后也就是最不重要的那一位开始

RadixSort(A,d)
	for i=1 to d
		使用稳定的排序方法对第i位排序

如果用计数排序，排一位需要Θ（n+k），排d位则需要Θ（d(n+k)）

桶排序

(输入是在[0, 1)上一致均匀分布)
将[0, 1) n等分，称为空桶
将n个输入分派到这些空桶之中
每个桶内排序
按顺序遍历每个桶中的元素

算法如下：
BucketSort(A)
　n=A.length
　让B[0……n-1]成为新数组
　for i=0 to n-1
　　让B[i]成为一个空列表
　for i=1 to n
　　将A[i]插入到列表B[ $\lfloor$ nA[i] $\rfloor$ ]
　for i=0 to n-1
　　对列表B[i]进行插入排序
　按顺序遍历每个桶中的元素并连接B[0]、B[1]、……B[n-1]

桶内排序
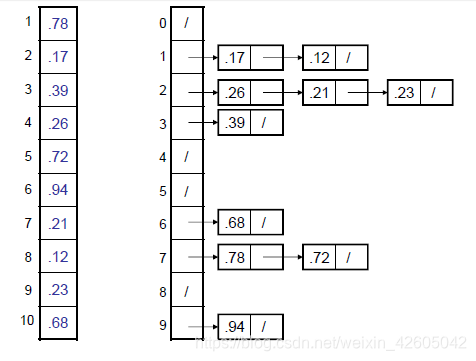
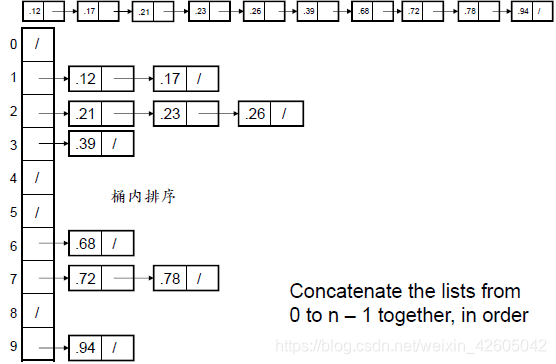
输入满足一致性随机分布,桶排序的平均运行开销为O(n)

参考：任课教师邱德红教授的课件

Shane恆

发布了25 篇原创文章 · 获赞 19 · 访问量 1万+

私信关注