算法设计与分析课程复习笔记2——递归关系

算法设计与分析课程复习笔记2——递归关系

递归关系

递归关系描述的是自然数上的函数关系
对于某个n>0的函数值，通过小于n的函数值表示出来

为什么要分析递归关系？
许多算法，特别是递归算法，时间开销函数都可以用递归关系来描述

求解方法

• 置换法（Substitution）
• 递归树（Recursion Tree）
• 迭代法（Iteration）
• 主方式（Master Theorem）

置换法

1. 猜想（经验、更换变元、先松后紧）
2. 验证猜想对于n= $n_0$的正确性
3. 验证猜想对于n> $n_0$的正确性

example：T(n) = 2T( $\lfloor$n/2 $\rfloor$) + n
猜想：T(n) = Θ(n lg n)
假设在n≥2时对于 $\lfloor$n/2 $\rfloor$成立,
即T( $\lfloor$n/2 $\rfloor$ )≤c $\lfloor$n/2 $\rfloor$lg( $\lfloor$n/2 $\rfloor$)

T(n)= 2T( $\lfloor$n/2 $\rfloor$ ) + n
≤2(c $\lfloor$n/2 $\rfloor$lg( $\lfloor$n/2 $\rfloor$ ))+n
≤cnlg(n/2)+n
=cnlgn-cnlg2+n
=cnlgn-cn+n
≤cnlgn 对于c>1

examples:
T(n) = 2T(n/2) +Θ(n) → T(n) = Θ(n lg n)
T(n) = 2T( $\lfloor$n/2 $\rfloor$) + n → T(n) = Θ(n lg n)
T(n) = 2T( $\lfloor$n/2 $\rfloor$+ 17) + n → T(n) = Θ(n lg n)

递归树

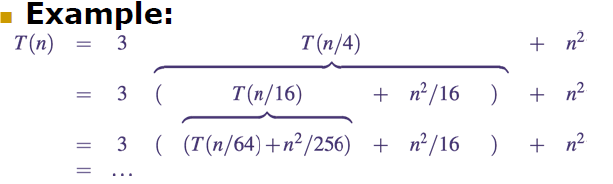
迭代法

1. 展开
2. 代数运算
3. 求和

example：
$T(n)=\left\{ \begin{aligned} c　ｎ＝１\\ aT(\frac nb)+cn　ｎ＞１ \end{aligned} \right.$

$T(n)=\left\{ \begin{aligned} Θ(n)　ａ＜ｂ\\ Θ(nlog_bn) 　ａ＝ｂ\\ Θ(n^{log_ba})　ａ＞ｂ\\ \end{aligned} \right.$

主方式

example:
$T(n)=9T(n/3)+n$
a=9
b=3
f(n)=n

$n^{log_ba}$= $n^{log_39}$=Θ（n²）
f(n)=O( $n^{log_39-ε}$）=n
ε=1,满足第一式

所以T（n）=Θ( $n^{log_ba}$)
T(n)=Θ( $n^2$)

重点：

• 置换法（Substitution）
• 递归树（Recursion Tree）
• 迭代法（Iteration）
• 主方式（Master Theorem）

参考：任课教师邱德红教授的课件