前回のレッスンではベクトル部分空間の列空間とヌル空間について説明しましたが、今回はヌル空間の特殊解、つまり Ax=0 の特殊解について説明します。特殊な解を解く核心は、消去法を使用して (行エシュロン形式) ステップ行列または (縮小行エシュロン形式/RREF) 最小行列を取得することです。
次に例を示します。たとえば、次の方程式系 Ax=0 があります。すべての x を解きます。つまり、行列 A を解きます。A は 3 つの方程式/3 つの制約、4 つの変数/4 つの自由度であることに注意してください。 、

(消去) 消去法を使用して行列を単純化します (行変換のみ)。
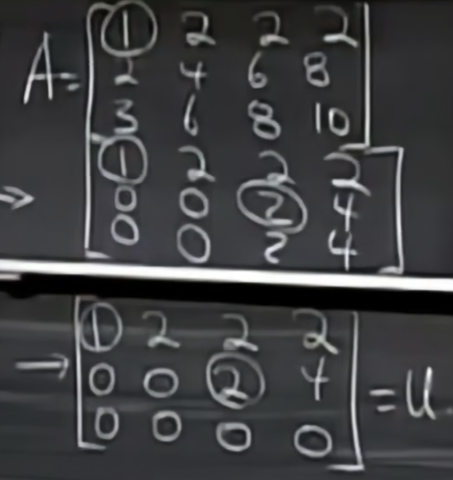
ステップ行列に変換します。ステップ行列の行数は、行列 A の (ランク) ランクと呼ばれます。ステップ行列の各行の、左から右へ 0 ではない最初の要素は (ピボット) ピボットと呼ばれ、列を (ピボット列) メイン列と呼び、マトリックス内のメイン列以外の列を (フリー列) フリー列と呼びます。観察を通じて、行列全体のすべての空き列はメイン列によって線形に表現できることがわかります。ピボットは、上の図では 1、2 としてマークされています。
では、Ax=0という特殊な解、つまり行列A列を分割した後の一次式係数はどのようにして求めるのでしょうか?空き列を単位方向ベクトルに割り当てることがよくあります。たとえば、空き列が 2 つある場合、[0, 1] と [1, 0] を空き列に割り当て、[0, 0, 1]、[0] を割り当てます。 ] を 3 つの自由列、1、0]、[1、0、0] に追加します。タイトルの通り、x2=1、x4=0とします。

空き額を特定の値 (x2=1、x4=0 など) に割り当てた後、行列または方程式系で逆置換を実行して、メイン列の係数 x1 と x3 を計算します。
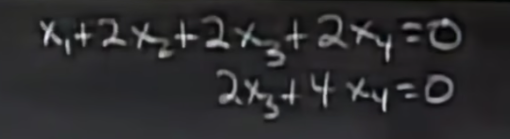
同様に、x2=0 と x4=1 の一次式係数を求め、2 番目の解を求めます。これら 2 つの線形独立解のすべての線形結合は、Ax=0 の特殊解、つまり x=c [-2, 1, 0, 0] + k [2, 0, -2, 1] です。

経験を通じて、方程式系が m*n、つまり m 個の方程式、n 個の未知量、ランクが r の場合、特殊な解に必要なベクトルに依存しないベクトルの数は nr であることがわかります。