0メモ
このブログ投稿は、2021年に教師に代わってLiYongleの基本コースのキーノートをまとめたものです。同済大学「工学数学:線形代数」第5版のカタログである李先生の教材によると、6つのセクションに分けて、それぞれのノートを適切な章。複雑な数式に遭遇した場合は、LaTeXを習得していないため、手書きの写真や教科書の数式のスクリーンショットをアップロードします(電話のカメラでは写真がはっきりと撮れない場合がありますが、コンテンツをできるだけ完全なものにするよう努めます) 。
このメモは、上記の教科書を体系的に整理したものではなく、将来の研究や研究にのみ適しています。
1行列式
覚えておくべき特別な公式はありません。
2マトリックスとその操作
1. A -1 Bを見つける:行列(A | B)を作成し、基本変換によって(E | X)に変換します。Xは必要なものです。
2. ABを探す-1:マトリックス(B構築T | A Tを)とに変換し(E | X)基本変形によって、およびX Tは、あなたが望むものです。
3. Aがn次行列の場合、①r(A)<k⇔Aのk次サブ式(存在する場合)はすべて0です。②r(A)≥k⇔Ak次サブ-式が存在するかどうか0;③A≠0⇔r(A)≥1;④r(A)=n⇔| A |≠0⇔Aは可逆行列です;⑤r(A)<n⇔| A | =0⇔A反転可能ではありません。
4. AとBはn次行列です。Aが可逆の場合、r(AB)= r(B)、r(BA)= r(B)です。
5. AとBはn次の行列で、max {r(A)、r(B)}≤r(A | B)≤r(A)+ r(B)です。
6.レッツA *その後、n次の行列Aの随伴行列である:①| A * | = | A | N-1 ;②A -1 = A * / | A |、③AA * = | A | E;④| kA | = k n | A |。
7. AとBはm×n次の行列です。n次の可逆行列Pとm次の可逆行列Qがあり、B = QAPである場合、AとBは等価と呼ばれ、A≌で表されます。 B。
8. AとBは次数m×nの行列であり、A≌B⇔r(A)= r(B)⇔Aは有限数の基本変換の後にBを取得できます。
9. A *をn次行列Aの随伴行列とすると、次のようになります。①r(A)= nの場合、r(A *)= n;②r(A)= n-1の場合、 r(A *)= 1;③r(A)≤n-2の場合、r(A *)= 0。
10、r(A T A)= r(A)= r(A T)= r(AA T)。
3行列の基本変換と線形方程式
1.n変数線形方程式系Ax = bの場合、次のようになります。①解なし⇔r(A)+ 1 = r(A | b);②一意の解⇔r(A)= r(A | b) = n;③無限に多くの解⇔r(A)= r(A | b)<n。
2.n変数の同次線形方程式Ax = 0の場合、次のようになります。①非ゼロの解があります⇔r(A)<n;②ゼロの解のみがあります⇔r(A)= n。
3.行列方程式AX = Bの解は⇔r(A)= r(A | B)です。
4.連立方程式の方程式の数が未知数の数より少ない場合、連立方程式にはゼロ以外の解が必要です。
5.有限数の基本行変換の後、AはBを取得し、次にA≌Bを取得し、PA = Bとなる可逆行列Pが存在する必要があります。AとBの列ベクトル:①は同じ線形相関を持ち、②は同じ線形表現を持ちます。
4ベクトルグループの線形相関
1. <α、β>はベクトルαとβの外積演算であり、<α、β> 2 = ||α|| 2・||β|| 2、等号はαとβの場合のみです。線形に関連している場合に確立されます。
3次元ベクトル空間において2、ベクトルの座標は、αせ及びβ塩基の同じセットである(下1、2、3)と(B 1、B 2、B 3それぞれ)、およびαせ及び角度は、次に、θの場合に挟まれるβ:
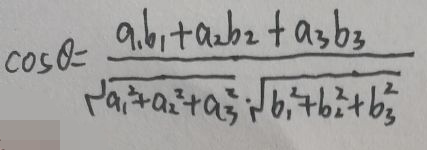
3レッツn次元ベクトルは、α 1 α、2、...、α nは次いでαペアワイズ直交する非ゼロのベクトルの集合であっても1、α 2、...、α nは線形独立なベクトルのグループがあります。
4.ベクトルグループⅠがベクトルグループⅡと同等であるための必要十分条件は、ベクトルグループⅠとベクトルグループⅡが互いに線形に表現できることである。
5.ベクトルグループⅠがベクトルグループⅡで線形表現できる場合、r(ベクトルグループⅠ)≤r(ベクトルグループⅡ)、ベクトルグループⅠがベクトルグループⅡで線形表現できる場合、およびベクトル内のベクトルの数グループⅠ>ベクトルグループII、ベクトルグループIのベクトルの数は、線形に関連している必要があります。ベクトルグループIが線形独立であり、ベクトルグループIがベクトルグループIIによって線形に表現できる場合、ベクトルグループIのベクトル≤ベクトルグループII番号のベクトル。
6.ベクトルグループⅠは、ベクトルグループⅡ⇔r(ベクトルグループⅠ)= r(ベクトルグループⅡ)= r(ベクトルグループⅠ、ベクトルグループⅡ)と同等です。
7. N + 1、n次元ベクトルは線形関係する必要があり、αベクトル群あれば1、α 2、...、α sはれる線形関係は、α 1、α 2、...、α S、...、α tはでなければなりません線形に関連している;ベクトルグループIが無関係であり、ベクトルグループIの各ベクトルの次元を拡張した後の高次元ベクトルグループがまだ無関係である場合。
図8に示すように、単一のベクター、α 1関連⇔α 1はゼロベクトルであり、二つのベクトルのα 1、α- 2関連⇔α 1、α- 2共線、3つのベクトル[アルファ] 。 1、α- 2、α- 3関連⇔α 。1、α- 2、α 3が同一平面。
9.ベクトルグループⅠのベクトルが単位ベクトルである場合、つまり各ベクトルのモジュラス長が1であり、ベクトルが互いに直交している場合、つまり内積が0である場合、ベクトルグループⅠは次のようになります。正規直交グループと呼ばれます。
5相似行列と2次形式
1. Aをn次の行列、αをn次元の非ゼロ列ベクトル、A・α=λ・αの場合、λは行列Aの固有値、αは行列Aの固有ベクトルとします。固有値λに対応します。
2.レッツAは①その後、微量のn次の行列であるA TR(A)=Σλ iはΣA= II ;②Πλ I = | A |。このように、A可逆⇔Aの固有値はゼロではありません。
3.行列Aの異なる固有値の固有ベクトルは線形独立です。Aがn次の実対称行列である場合、Aの異なる固有値の固有ベクトルはペアワイズ直交です。
4. AとBの両方がn次行列であると仮定すると、P -1 AP = Bとなるような可逆行列Pが存在する場合、A〜Bとなります。
5. A〜Bの場合、①|λE-A| = |λE-B|であり、AとBの固有値はまったく同じです;②r(A)= r(B);③| A | = | B |;④tr(A)= tr(B)。
前記三次マトリックスAは、同様に行列Λに対角化することができる場合には、Aの固有値をλ 1 λ、2、及びλ 3形態Aの対角行列Λ= DIAG(λ 1、λ 2、λ 3)、Aに対応する固有ベクトルはrは1、R 2、及びR 3のλ 1 λ、2、及びλ 3形可逆行列P =(R 1、R 2、R 3)、およびP -1 AP =λ 、つまり、A〜Λ。
7、三次行列Aは、3個の独立した固有ベクトルR&LTを有する場合。1は、R 2は、R 3、R&LTミート・A I =λはI・R&LT I Iは= l、2、3。すなわち、A(rは1、R 2、R 3)=(λ 1・R 1、λ 2・R 2、λ 3・R 3)=(R 1、R 2、R 3)・DIAG(λ 1、λ 2、λ 3)、P =(Rせ1、R 2、R 3)、λ= DIAG(λ 1、λ 2、λ 3)、次いで、AP =Pλ、である、P -1 AP =Λ。要するに、n次行列Aは同様に対角化することができます⇔Aはn個の無関係な固有ベクトルを持っています。
8. n次行列Aがn個の異なる固有値を持つ場合、Aは同様に対角化する必要があります。λがAのk倍の固有値である場合、λは最大でk個の無関係な固有ベクトルに対応します。λが行列Aのk倍の固有値の場合、λはk個の独立した固有ベクトルに対応します。
9. Aがn次の実対称行列である場合、Aの固有値はすべて実数です。
10. Aがオーダーの直交行列PであるN、Pそうしなければならないことが、順序の任意実対称行列であり、N -1 AP =Λ= DIAG(λ 1、λ 2、...、λ N)。
11.二次形式とその行列は次のように表されます。行列Aのランクは二次形式のランクです:
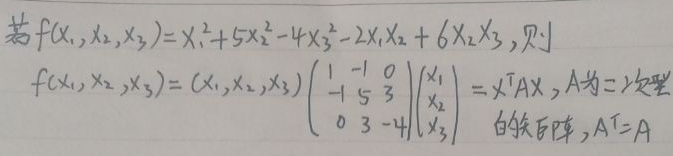
12。二次形式の標準形式には二次項のみがあり、混合項はありません:

13。の標準形式二次形式は最初に標準タイプである必要があります。つまり、二次項のみがあり、混合項はなく、2番目の二次項の係数は次のように-1,0、+ 1のみです
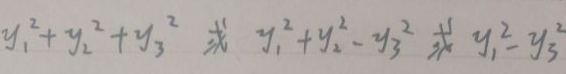
。標準タイプの場合、正の慣性指数をpとして、二次慣性指数をqとして記録します。上図の3つの二次形式の場合、[p = 3、q = 0]、[p = 2、q = 1]、および[p = 1、q = 1]です。
15.二次変換:

16。契約:C T AC = Bの場合、Cは可逆であり、AとBの間の契約と呼ばれ、A≃Bとして記録されます。
17.座標変換により、任意の2次形式を標準形式に変換できます。マッチング方法と直交変換方法の2つの方法があります。
任意の二次形態F = xについて18 T A AX、T = Aは、Pは直交行列である直交変換X = Pyは、標準的なフォームは、X二次形式なって、常に存在するTアックス= Y T λyとを= Σλ I・Y I 2 λ、iはAのn個の固有値であります
19.二次形式の正準形式は一意です(慣性の定理):任意の二次形式x T Axの場合、正と負の慣性指数は、座標変換に変換された標準形式で一意に決定されます。
20.正定値二次形式:二次形式f(x)= x T Axを設定します。ゼロ以外のベクトルx =(x 1、x 2、…、x n)Tの場合、常にf(x)が存在します。 > 0の場合、f(x)は正定値二次形式と呼ばれ、対応する行列Aは正定値行列と呼ばれます。
21.二次形式は、座標変換後の正定性を変化させない:座標変換X = Cyの下で、二次形式は、x T Axが有する同様の正定性二次形式のY T C T ACYを。
22.二次正定値の必要条件は、すべての主対角要素a ii > 0であるということです。二次正定値に必要かつ十分な条件:①二次f(x)= x T Ax正定値;②標準形式のf(x)の二乗係数はすべて0より大きい;③正の慣性指数p = n; ④AとEの契約、つまりリバーシブルCがあるため、C T AC = E、A≃E;⑤Aの固有値はすべて0より大きい;⑥Aの連続するプリンシパルとサブフォームはすべてより大きい0。
23.正定値のn次の実対称行列Aに必要な条件は、| A |> 0です。正定n次実対称行列Aの必要十分条件:①AとEが縮約します。つまり、C T AC = E、A≃E;②Aの正の慣性指数が次のように反転可能なCが存在します。 Nに等しく、0より大きい;④Aの固有値は0より大きい;⑤、可逆Uあるので、A = U T U.
24.相似行列は、同じ固有値、特性多項式、行列式、ランク、およびトレースを持ちます。
25. Aはn次の行列である場合、AのR異なる固有値をλであるとする1、λ 2、...、λ R、及び対応する複数のルート数がpである1、P 2、...、 P R Pと呼ばれ、Iは、λであるI代数再現、のλ I、λに対応する特徴空間の次元、すなわちIの独立したベクトルの数が幾何学的反復と呼ばれます。
26.λ行列の逆行列とデジタル行列(可逆の場合)は両方とも次のとおりです。A -1 = A * / | A |。
27.任意のλ行列が可逆であるための必要十分条件は、その行列式が非ゼロ定数であるということです。
28.λ行列A(λ)のランクをrとします。①行列式係数:正の整数1≤k≤rの場合、A(λ)はゼロ以外のk次のサブ式を持つ必要があります。 A(λ)のがゼロ以外であるk次の部分式の1次係数が1である最大公約数D k(λ)は、A(λ)のk次行列式因子と呼ばれます。② A(λ)の
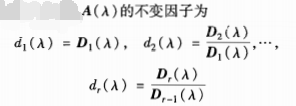
単因子:フルランクのn次λ行列A(λ)の場合、πd・C I(λ)= | a(λ)|、 Cは非ゼロ定数であり、すべてのD I数(λ)およびa = n;③は基本因子による定数因子ではありません。1の不変因子は項に分割されます。次に例を示します

。29 。両方がAとBはn次のデジタル行列であり、AからBの必要条件と十分な条件は次のとおりです。①λE-A≌λE-B;②λE-AλE-Bと同じシュミット標準形式です;③λE-AとλE-Bの定数係数は同じです。④λE-AとλE-Bの行列式係数は同じです。⑤λE-AとλE-Bの基本係数は同じです。
30.デジタル行列Aの場合、λE-Aの不変因子はAの不変因子と呼ばれ、λE-Aの基本因子はAの基本因子と呼ばれます。
31、Aがn次行列の場合、与えられたランクλE-Aは同じ係数rであり、λE-AはD I(λ)、I = R&lt .... 1です。その場合、λE-Aのシュミット標準タイプは次のとおりです。

6線形空間と線形変換
1.ベクトルグループ(α 1、α 2、α 3)と(β 1、β 2、β 3 IF(β)は、3次元ベクトル空間内の2個の異なる塩基である1、β 2、β 3)= (α 1、α 2、α 3)・P、次にPが呼び出された遷移行列ベクトル群から、(α 1、α 2、α 3)(βに対する1、β 2、β 3)。P =(β 1、β 2、β 3)-1・(α 1、α 2、α 3)。
2.同じ線形変換の異なる基底の下にある行列は類似しており、類似した行列は同じ固有値、特性多項式、行列式、ランク、およびトレースを持っています。
3、セットV 1、V 2がV場合、二つのサブ空間Vの線形空間である。1 ∩V 2 = {0}ベクトルと呼ばれるV 1及びV 2と空間V 1 + V 2真っ直ぐであり、Vと称される1 ⊕V 2。次の命題は等価である:①V 1 + V 2直和である。②DIM(V 1 + V 2)= DIM(V 1)+ DIM(V 2);③ベクトル群がⅠの場合基づいVの1、ベクトルグループⅱである基準Vの2は、{ベクトル群ⅰ、ベクトル群はⅱ}である基底Vの1 + V 2。
4. WをVの部分空間とし、α∈Vを取ります。任意のβ∈Wに対してα⊥βがある場合、それはα⊥Wと呼ばれます。
5.ピタゴラスの定理:α及びβの両方が非ゼロベクトル、及びα⊥βである場合、||α+β|| = ||α-β|| = ||α|| 2 + ||β| | 2。
数えてみると、ちょうど60音あることに気づきました。
終わり