Soy Yuantongxue. Este artículo se basa en el contenido del libro "Algoritmos y programas de modelado matemático" escrito por el Sr. Si Shoukui, usando los ejemplos del libro. Los lenguajes de programación en el libro son MATLAB y Lingo. Usa Python para resolver el problema. Durante el próximo mes aprenderé a usar Python para resolver problemas de modelado matemático. Se registrarán notas y algunos casos durante el estudio.

1. Programación lineal

1.1 Ejemplos y definiciones de programación lineal

Ejemplo 1 Una fábrica de máquinas herramienta produce dos tipos de máquinas herramienta A y B, y la ganancia después de cada venta es de 4000 yuanes y 3000 yuanes respectivamente. La producción de la máquina herramienta A debe ser procesada por las máquinas A y B, y el tiempo de procesamiento es de 2 horas y 1 hora para cada máquina. Si el número de horas de máquina disponibles para procesamiento por día es de 10 horas para la máquina A, 8 horas para la máquina B y 7 horas para la máquina C, ¿cuántas máquinas herramienta A y B debe producir la fábrica para maximizar la ganancia total?

Modelo matemático del problema anterior: suponiendo que la fábrica produce $x_{1}$ la $x_{2}$ mayor ganancia total al producir las máquinas A y B, $x_{1}, x_{2}$ debería satisfacer:

Las variables aquí se $x_{1}, x_{2}$ denominan variables de decisión, (1) se denomina función objetivo del problema y varias desigualdades en (2) son las restricciones del problema, indicadas como st (es decir, sujetas a). Dado que la función objetivo y las restricciones anteriores son funciones lineales, se denomina problema de programación lineal. En resumen, un problema de programación lineal es un problema de encontrar el máximo o mínimo de una función objetivo lineal bajo las restricciones de un conjunto de restricciones lineales.

1.2 Use la biblioteca scipy en Python para resolver el problema de programación lineal de la columna 1:

La forma estándar de programación lineal es

$\begin{reunidos} \min c^{T} x \\ \text { st }\left\{\begin{array}{l} A x \leq b \\ A eq \cdot x=beq \\ lb \ leq x \leq ub \end{matriz}\right. \end{reunidos}$ (3)

Entre ellos, c es el vector de valor; A y b corresponden a restricciones de desigualdad lineal; Aeq y beq corresponden a restricciones de igualdad lineal; los límites corresponden a lb y ub en la fórmula, los límites inferior y superior del vector de decisión.

scipy.optimize.linprog( c , A_ub=Ninguno , b_ub=Ninguno , A_eq=Ninguno , b_eq=Ninguno , límites=Ninguno , método='simple' , callback=Ninguno , opciones=Ninguno )

Análisis de parámetros de entrada:

c: coeficientes de la función objetivo lineal
A_ub (parámetro opcional): matriz de restricciones de desigualdad, $A_{ub}$ cada fila especifica los coeficientes de las restricciones de desigualdad lineal en x
b_ub (parámetro opcional): vector de restricciones de desigualdad, cada elemento representa $A_{ub}$ el límite superior de x
A_eq (parámetro opcional): matriz de restricciones de igualdad, $A_{equivalente}$ cada fila especifica los coeficientes de las restricciones de igualdad lineal en x xx
b_eq (parámetro opcional): vector de restricciones de igualdad, $A_{equivalente}$ cada elemento del cual debe ser igual al $b_{eq}$ elemento correspondiente
límites (parámetro opcional): define el valor mínimo y máximo de la variable de decisión x
- Tipo de datos: (mín., máx.) par de secuencias
- Ninguno: use Ninguno para no tener límites, por defecto los límites son (0, Ninguno) (todas las variables de decisión no son negativas)
- Si se proporciona una tupla (mín., máx.), los valores mínimo y máximo se utilizarán como límites para todas las variables de decisión.

Análisis de parámetros de salida:

x: el valor de la variable de decisión que minimiza la función objetivo mientras satisface las restricciones
diversión: el valor óptimo de la función objetivo ( $c^{^{T}}x$ )
holgura: valor de holgura para las restricciones de desigualdad (nominalmente positivo) $b_{ub}-A_{ub}x$
con: residuos para restricciones de igualdad (nominalmente cero) $b_{eq}-A_{eq}x$
éxito: verdadero cuando el algoritmo encontró con éxito la mejor solución
estado: un número entero que representa el estado de salida del algoritmo
- 0: la optimización finalizó con éxito
- 1 : límite de iteraciones alcanzado
- 2: El problema no parece factible
- 3: El problema parece ser la falta de convergencia
- 4: Dificultades numéricas encontradas
nit: número total de iteraciones realizadas en todas las etapas
mensaje: descriptor de cadena del estado de salida del algoritmo

Use la biblioteca scipy para resolver el ejemplo 1:

from scipy.optimize import linprog
c = [-4, -3]   #目标函数的系数
A= [[2, 1], [1, 1],[0,1]]  #<=不等式左侧未知数系数矩阵
b = [10,8,7]    # <=不等式右侧常数矩阵
#A_eq = [[]]   #等式左侧未知数系数矩阵
#B_eq = []     #等式右侧常数矩阵
x1 = [0, None]  #未知数取值范围
x2 = [0, None]  #未知数取值范围
res =linprog(c, A, b, bounds=(x1, x2))#默认求解最小值，求解最大值使用-c并取结果相反数
print(res)

Resultado de salida:

     con: array([], dtype=float64)
     fun: -25.999999999841208
 message: 'Optimization terminated successfully.'
     nit: 5
   slack: array([8.02629074e-11, 3.92663679e-11, 1.00000000e+00])
  status: 0
 success: True
       x: array([2., 6.])

fun es el valor óptimo de la función objetivo, slack es la variable de holgura, status es el estado del resultado de la optimización y x es la solución óptima.

El resultado solución de este modelo es: cuando x1=2, x2=6, la función obtiene el valor óptimo de 25.999999999841208.

Ejemplo 2 Resuelva el siguiente problema de programación lineal:

$\begin{reunidos} \max z=2x_{1}+3x_{2}-5x_{3} \\ \text { st }\left\{\begin{matriz}{l}x _{1}+x _ {2}+x _{3}=7 \\2x _{1}-5x _{2}+x _{3}\geq 10 \\x _{1}+3x _{2}+x _{{ 3}\leq 12 \\ x _{1},x _{2},x _{3}\geq 0 \end{matriz}\right. \end{reunidos}$

¡Cuidado con estandarizar primero!

Aquí hay otra forma más canónica de escribir:

from scipy import optimize
import numpy as np
c = np.array([2,3,-5])
A = np.array([[-2,5,-1],[1,3,1]])
B = np.array([-10,12])
Aeq = np.array([[1,1,1]])
Beq = np.array([7])
x1 = [0, None]  #未知数取值范围
x2 = [0, None]  #未知数取值范围
x3 = [0, None]  #未知数取值范围
res = optimize.linprog(-c,A,B,Aeq,Beq,bounds=(x1, x2, x3))
print(res)

Resultado de salida:

     con: array([1.80713489e-09])
     fun: -14.571428565645054
 message: 'Optimization terminated successfully.'
     nit: 5
   slack: array([-2.24579466e-10,  3.85714286e+00])
  status: 0
 success: True
       x: array([6.42857143e+00, 5.71428571e-01, 2.35900788e-10])

El resultado solución de este modelo es: cuando x1=6.4, x2=5.7, x3=2.3, la función obtiene el valor óptimo de 14.571428565645054

Ejemplo 3 Resolviendo un problema de programación lineal:

$\begin{reunidos} \min z=2x_{1}+3x_{2} + x_{3} \\ \text { st }\left\{\begin{matriz}{l}x _{1}+4x _ {2}+2x _{3} \geq 8 \\ 3x _{1} + 2x _{2} \geq 6 \\ x _{1},x _{2},x _{3}\geq 0 \end{matriz}\right. \end{reunidos}$

Escrito en Python:

from scipy import optimize
import numpy as np
c = np.array([2,3,1])
A = np.array([[1,4,2],[3,2,0]])
B = np.array([8,6])
x1 = [0, None]  #未知数取值范围
x2 = [0, None]  #未知数取值范围
x3 = [0, None]  #未知数取值范围
res = optimize.linprog(c,-A,-B,bounds=(x1, x2, x3))
print(res)

Resultado de salida:

     con: array([], dtype=float64)
     fun: 6.999999994872993
 message: 'Optimization terminated successfully.'
     nit: 3
   slack: array([ 3.85261245e-09, -1.41066261e-08])
  status: 0
 success: True
       x: array([1.17949641, 1.23075538, 0.94874104])

El resultado solución de este modelo es: cuando x1=1.1, x2=1.2, x3=0.9, la función obtiene el valor óptimo de 6.999999994872993

2. Problemas de transporte

2.1 Modelado matemático del proceso de producción y balance de ventas:

Ejemplo 6 Una mercancía tiene $metro$ un lugar de origen y $norte$ un lugar de venta, la producción de cada lugar de producción es $a_{1},... ,a_{m}$ y la demanda de cada lugar de venta es $b_{1},... ,b_{n}$ . Si la tarifa unitaria de flete del producto desde el lugar de $i$ origen hasta el lugar de venta es , ¿cómo se debe ajustar el transporte para que el costo total del flete sea el más económico? $j$ $c_{ij}$

Solución: Introducir una variable $x_{ij}$ cuyo valor sea la cantidad de la mercancía $i$ embarcada desde el lugar de origen hasta $j$ el lugar de venta El modelo matemático es

$\begin{array}{l} \min \sum_{i=1}^{m} \sum_{j=1}^{n} c_{ij} x_{ij} \\ \text { st }\left\ {\begin{matriz}{l} \sum_{j=1}^{n} x_{ij}=a_{i}, \quad i=1, \cdots, m \\ \sum_{i=1}^ {m} x_{ij}=b_{j}, \quad j=1,2, \cdots, n \\ x_{ij} \geq 0 \end{matriz}\right. \end{matriz}$

Obviamente un problema de programación lineal, que por supuesto puede ser resuelto por el método simplex.

Para el problema de transporte de balance de producción y ventas, existen las siguientes relaciones:

$\sum_{j=1}^{n} b_{j}=\sum_{i=1}^{m}\left(\sum_{j=1}^{n} x_{ij}\right)=\ suma_{j=1}^{n}\left(\sum_{i=1}^{m} x_{ij}\right)=\sum_{i=1}^{m} a_{i}$

La matriz de coeficientes de sus restricciones es bastante especial, y se puede utilizar un método de cálculo relativamente simple, que habitualmente se denomina método de tarea sobre la mesa (propuesto por Kantorovich y Hitchcock de forma independiente, denominado método de trabajo de la mesa de Kang-Hitch), lo siguiente usa un ejemplo para explicar.

2.2 El problema del transporte de la producción y el balance de ventas

1. Descripción del problema

Una empresa tiene tres fábricas, A, B y C, que suministran productos respectivamente a A, B, C y D. La producción, la demanda y la tasa de flete (unidad: yuan/tonelada) desde la fábrica hasta las lugar son los siguientes Como se muestra, encuentre el mejor plan de transporte que minimice el costo.

fábrica \ ventas	A	B	C	D	Producción (toneladas)
Primero	8	6	10	9	18
Segundo	9	12	13	1	18
C	14	12	dieciséis	5	19
Ventas (toneladas)	dieciséis	15	7	17	55

2. Análisis de problemas

Salida total=18+18+19=55

Ventas totales=16+15+7+17=55

La salida es igual a las ventas, es decir, es un problema de transporte del equilibrio entre producción y ventas. Resuelva directamente usando el método de trabajo en la tabla.

3. Usa Python para resolver:

# 运输问题求解：使用Vogel逼近法寻找初始基本可行解
import numpy as np
import copy
import pandas as pd


def main():
    # mat = pd.read_csv('表上作业法求解运输问题.csv', header=None).values
    # mat = pd.read_excel('表上作业法求解运输问题.xlsx', header=None).values
    a = np.array([18, 18, 19])  # 产量
    b = np.array([16, 15, 7, 17])  # 销量
    c = np.array([[8, 6, 10, 9], [9, 12, 13, 7], [14, 12, 16, 5]])
    # [c, x] = TP_vogel(mat)
    [c,x]=TP_vogel([c,a,b])


def TP_split_matrix(mat):  # 运输分割矩阵
    c = mat[:-1, :-1]
    a = mat[:-1, -1]
    b = mat[-1, :-1]
    return (c, a, b)


def TP_vogel(var):  # Vogel法代码，变量var可以是以numpy.ndarray保存的运输表，或以tuple或list保存的(成本矩阵,供给向量,需求向量)
    import numpy
    typevar1 = type(var) == numpy.ndarray
    typevar2 = type(var) == tuple
    typevar3 = type(var) == list
    if typevar1 == False and typevar2 == False and typevar3 == False:
        print('>>>非法变量<<<')
        (cost, x) = (None, None)
    else:
        if typevar1 == True:
            [c, a, b] = TP_split_matrix(var)
        elif typevar2 == True or typevar3 == True:
            [c, a, b] = var
        cost = copy.deepcopy(c)
        x = np.zeros(c.shape)
        M = pow(10, 9)
        for factor in c.reshape(1, -1)[0]:
            p = 1
            while int(factor) != M:
                if np.all(c == M):
                    break
                else:
                    print('第1次迭代！')
                    print('c:\n', c)
                    # 获取行/列最小值数组
                    row_mini1 = []
                    row_mini2 = []
                    for row in range(c.shape[0]):
                        Row = list(c[row, :])
                        row_min = min(Row)
                        row_mini1.append(row_min)
                        Row.remove(row_min)
                        row_2nd_min = min(Row)
                        row_mini2.append(row_2nd_min)
                    # print(row_mini1,'\n',row_mini2)
                    r_pun = [row_mini2[i] - row_mini1[i] for i in range(len(row_mini1))]
                    print('行罚数：', r_pun)
                    # 计算列罚数
                    col_mini1 = []
                    col_mini2 = []
                    for col in range(c.shape[1]):
                        Col = list(c[:, col])
                        col_min = min(Col)
                        col_mini1.append(col_min)
                        Col.remove(col_min)
                        col_2nd_min = min(Col)
                        col_mini2.append(col_2nd_min)
                    c_pun = [col_mini2[i] - col_mini1[i] for i in range(len(col_mini1))]
                    print('列罚数：', c_pun)
                    pun = copy.deepcopy(r_pun)
                    pun.extend(c_pun)
                    print('罚数向量：', pun)
                    max_pun = max(pun)
                    max_pun_index = pun.index(max(pun))
                    max_pun_num = max_pun_index + 1
                    print('最大罚数：', max_pun, '元素序号：', max_pun_num)
                    if max_pun_num <= len(r_pun):
                        row_num = max_pun_num
                        print('对第', row_num, '行进行操作：')
                        row_index = row_num - 1
                        catch_row = c[row_index, :]
                        print(catch_row)
                        min_cost_colindex = int(np.argwhere(catch_row == min(catch_row)))
                        print('最小成本所在列索引：', min_cost_colindex)
                        if a[row_index] <= b[min_cost_colindex]:
                            x[row_index, min_cost_colindex] = a[row_index]
                            c1 = copy.deepcopy(c)
                            c1[row_index, :] = [M] * c1.shape[1]
                            b[min_cost_colindex] -= a[row_index]
                            a[row_index] -= a[row_index]
                        else:
                            x[row_index, min_cost_colindex] = b[min_cost_colindex]
                            c1 = copy.deepcopy(c)
                            c1[:, min_cost_colindex] = [M] * c1.shape[0]
                            a[row_index] -= b[min_cost_colindex]
                            b[min_cost_colindex] -= b[min_cost_colindex]
                    else:
                        col_num = max_pun_num - len(r_pun)
                        col_index = col_num - 1
                        print('对第', col_num, '列进行操作：')
                        catch_col = c[:, col_index]
                        print(catch_col)
                        # 寻找最大罚数所在行/列的最小成本系数
                        min_cost_rowindex = int(np.argwhere(catch_col == min(catch_col)))
                        print('最小成本所在行索引：', min_cost_rowindex)
                        # 计算将该位置应填入x矩阵的数值（a,b中较小值）
                        if a[min_cost_rowindex] <= b[col_index]:
                            x[min_cost_rowindex, col_index] = a[min_cost_rowindex]
                            c1 = copy.deepcopy(c)
                            c1[min_cost_rowindex, :] = [M] * c1.shape[1]
                            b[col_index] -= a[min_cost_rowindex]
                            a[min_cost_rowindex] -= a[min_cost_rowindex]
                        else:
                            x[min_cost_rowindex, col_index] = b[col_index]
                            # 填入后删除已满足/耗尽资源系数的行/列，得到剩余的成本矩阵，并改写资源系数
                            c1 = copy.deepcopy(c)
                            c1[:, col_index] = [M] * c1.shape[0]
                            a[min_cost_rowindex] -= b[col_index]
                            b[col_index] -= b[col_index]
                    c = c1
                    print('本次迭代后的x矩阵：\n', x)
                    print('a:', a)
                    print('b:', b)
                    print('c:\n', c)
                if np.all(c == M):
                    print('【迭代完成】')
                    print('-' * 60)

                else:
                    print('【迭代未完成】')
                    print('-' * 60)

                    p += 1
                    print(f"第{p}次迭代！")
        total_cost = np.sum(np.multiply(x, cost))
        if np.all(a == 0):
            if np.all(b == 0):
                print('>>>供求平衡<<<')
            else:
                print('>>>供不应求，需求方有余量<<<')
        elif np.all(b == 0):
            print('>>>供大于求，供给方有余量<<<')
        else:
            print('>>>无法找到初始基可行解<<<')
        print('>>>初始基本可行解x*：\n', x)
        print('>>>当前总成本：', total_cost)
        [m, n] = x.shape
        varnum = np.array(np.nonzero(x)).shape[1]
        if varnum != m + n - 1:
            print('【注意：问题含有退化解】')
    return (cost, x)


if __name__ == '__main__':
    main()

Resultado de salida:

D:\Anaconda\python.exe D:/PyCharm/数学建模/线性规划/www.py
第1次迭代！
c:
 [[ 8  6 10  9]
 [ 9 12 13  7]
 [14 12 16  5]]
行罚数： [2, 2, 7]
列罚数： [1, 6, 3, 2]
罚数向量： [2, 2, 7, 1, 6, 3, 2]
最大罚数： 7 元素序号： 3
对第 3 行进行操作：
[14 12 16  5]
最小成本所在列索引： 3
本次迭代后的x矩阵：
 [[ 0.  0.  0.  0.]
 [ 0.  0.  0.  0.]
 [ 0.  0.  0. 17.]]
a: [18 18  2]
b: [16 15  7  0]
c:
 [[         8          6         10 1000000000]
 [         9         12         13 1000000000]
 [        14         12         16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第2次迭代！
第1次迭代！
c:
 [[         8          6         10 1000000000]
 [         9         12         13 1000000000]
 [        14         12         16 1000000000]]
行罚数： [2, 3, 2]
列罚数： [1, 6, 3, 0]
罚数向量： [2, 3, 2, 1, 6, 3, 0]
最大罚数： 6 元素序号： 5
对第 2 列进行操作：
[ 6 12 12]
最小成本所在行索引： 0
本次迭代后的x矩阵：
 [[ 0. 15.  0.  0.]
 [ 0.  0.  0.  0.]
 [ 0.  0.  0. 17.]]
a: [ 3 18  2]
b: [16  0  7  0]
c:
 [[         8 1000000000         10 1000000000]
 [         9 1000000000         13 1000000000]
 [        14 1000000000         16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第3次迭代！
第1次迭代！
c:
 [[         8 1000000000         10 1000000000]
 [         9 1000000000         13 1000000000]
 [        14 1000000000         16 1000000000]]
行罚数： [2, 4, 2]
列罚数： [1, 0, 3, 0]
罚数向量： [2, 4, 2, 1, 0, 3, 0]
最大罚数： 4 元素序号： 2
对第 2 行进行操作：
[         9 1000000000         13 1000000000]
最小成本所在列索引： 0
本次迭代后的x矩阵：
 [[ 0. 15.  0.  0.]
 [16.  0.  0.  0.]
 [ 0.  0.  0. 17.]]
a: [3 2 2]
b: [0 0 7 0]
c:
 [[1000000000 1000000000         10 1000000000]
 [1000000000 1000000000         13 1000000000]
 [1000000000 1000000000         16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第4次迭代！
第1次迭代！
c:
 [[1000000000 1000000000         10 1000000000]
 [1000000000 1000000000         13 1000000000]
 [1000000000 1000000000         16 1000000000]]
行罚数： [999999990, 999999987, 999999984]
列罚数： [0, 0, 3, 0]
罚数向量： [999999990, 999999987, 999999984, 0, 0, 3, 0]
最大罚数： 999999990 元素序号： 1
对第 1 行进行操作：
[1000000000 1000000000         10 1000000000]
最小成本所在列索引： 2
本次迭代后的x矩阵：
 [[ 0. 15.  3.  0.]
 [16.  0.  0.  0.]
 [ 0.  0.  0. 17.]]
a: [0 2 2]
b: [0 0 4 0]
c:
 [[1000000000 1000000000 1000000000 1000000000]
 [1000000000 1000000000         13 1000000000]
 [1000000000 1000000000         16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第5次迭代！
第1次迭代！
c:
 [[1000000000 1000000000 1000000000 1000000000]
 [1000000000 1000000000         13 1000000000]
 [1000000000 1000000000         16 1000000000]]
行罚数： [0, 999999987, 999999984]
列罚数： [0, 0, 3, 0]
罚数向量： [0, 999999987, 999999984, 0, 0, 3, 0]
最大罚数： 999999987 元素序号： 2
对第 2 行进行操作：
[1000000000 1000000000         13 1000000000]
最小成本所在列索引： 2
本次迭代后的x矩阵：
 [[ 0. 15.  3.  0.]
 [16.  0.  2.  0.]
 [ 0.  0.  0. 17.]]
a: [0 0 2]
b: [0 0 2 0]
c:
 [[1000000000 1000000000 1000000000 1000000000]
 [1000000000 1000000000 1000000000 1000000000]
 [1000000000 1000000000         16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第6次迭代！
第1次迭代！
c:
 [[1000000000 1000000000 1000000000 1000000000]
 [1000000000 1000000000 1000000000 1000000000]
 [1000000000 1000000000         16 1000000000]]
行罚数： [0, 0, 999999984]
列罚数： [0, 0, 999999984, 0]
罚数向量： [0, 0, 999999984, 0, 0, 999999984, 0]
最大罚数： 999999984 元素序号： 3
对第 3 行进行操作：
[1000000000 1000000000         16 1000000000]
最小成本所在列索引： 2
本次迭代后的x矩阵：
 [[ 0. 15.  3.  0.]
 [16.  0.  2.  0.]
 [ 0.  0.  2. 17.]]
a: [0 0 0]
b: [0 0 0 0]
c:
 [[1000000000 1000000000 1000000000 1000000000]
 [1000000000 1000000000 1000000000 1000000000]
 [1000000000 1000000000 1000000000 1000000000]]
【迭代完成】
------------------------------------------------------------
>>>供求平衡<<<
>>>初始基本可行解x*：
 [[ 0. 15.  3.  0.]
 [16.  0.  2.  0.]
 [ 0.  0.  2. 17.]]
>>>当前总成本： 407.0

进程已结束，退出代码为 0

El método utilizado anteriormente es el método de trabajo sobre la mesa, que se muestra a continuación:

Coste total óptimo final: 407,0

2.3 El problema del transporte donde la producción supera las ventas

1. Descripción del problema

Hay tres bases de cría de animales que proporcionan leche fresca a las ciudades 4. La demanda diaria de leche fresca en las ciudades 4, el suministro diario de leche fresca en las bases 3 y el costo de entregar leche fresca por kilolitro se muestran en la tabla a continuación. Trate de determinar la solución de transporte de leche fresca más económica.

ciudad\base	A	B	C	D	Suministro
Primero	3	2	4	5	30
Segundo	2	3	5	3	40
C	1	4	2	4	50
pedir	dieciséis	30	veinticuatro	30

2. Análisis de problemas

Suministro total=30+40+50=120

Demanda total=16+30+24+30=100

Sobreoferta, es decir, la producción excede las ventas, lo cual es un problema de transporte donde la producción excede las ventas. Para transformar el problema en un problema de transporte de producción y ventas equilibradas, es necesario realizar los siguientes ajustes.

(1) Agregue un lugar de venta virtual E, de modo que la demanda total sea 120-100=20.

(2) Dado que el lugar de venta es virtual, de hecho, los materiales con exceso de producción se almacenan in situ en el lugar de origen, por lo que no habrá transporte real, es decir, no se incurrirá en fletes.

Por lo tanto, la nueva tabla de oferta y demanda y tarifa unitaria es la siguiente.

ciudad\base	A	B	C	D	Y	Suministro
Primero	3	2	4	5	0	30
Segundo	2	3	5	3	0	40
C	1	4	2	4	0	50
pedir	dieciséis	30	veinticuatro	30	20	120

3. Resolución de problemas

Usando python para lograr:

Esto también se puede resolver usando el (método del elemento mínimo):

'----------------------------------------最小元素法------------------------------------' \
'最小元素法是指有限满足单位运价最小的供销服务'
import numpy as np
import copy

supplyNum = 3  # 供应商数量
demandNum = 5  # 需求商数量
A = np.array([30,40,50])  # 产量
B = np.array([16,30,24,30,20])  # 销量
C = np.array([[3,2,4,5,0], [2,3,5,3,0], [1,4,2,4,0]])  # 成本
X = np.zeros((supplyNum, demandNum))  # 初始解
c = copy.deepcopy(C)
maxNumber = 10000  # 极大数


def pivot(A, B, c, X):
    index = np.where(c == np.min(c))  # 寻找最小值的索引
    minIndex = (index[0][0], index[1][0])  # 确定最小值的索引
    # 确定应该优先分配的量，并且改变价格
    if A[index[0][0]] > B[index[1][0]]:
        X[minIndex] = B[index[1][0]]
        c[:, index[1][0]] = maxNumber  # 改变价格
        A[index[0][0]] = A[index[0][0]] - B[index[1][0]]
        B[index[1][0]] = 0  # 改变销量
    else:
        X[minIndex] = A[index[0][0]]
        c[index[0][0], :] = maxNumber
        B[index[1][0]] = B[index[1][0]] - A[index[0][0]]
        A[index[0][0]] = 0
    return A, B, c, X


# 最小元素法
def minimumElementMethod(A, B, c, X):
    while (c < maxNumber).any():
        A, B, c, X = pivot(A, B, c, X)
    return X


solutionMin = minimumElementMethod(A, B, c, X)
print('最小元素法得到的初始解为：')
print(solutionMin)
print('最小元素法得到的总运费为:', ((solutionMin * C).sum()))

Resultado de salida:

最小元素法得到的初始解为：
[[ 0. 10.  0.  0. 20.]
 [ 0. 20.  0. 20.  0.]
 [16.  0. 24. 10.  0.]]
最小元素法得到的总运费为: 244.0

2.4 El problema del transporte que la producción es menor que las ventas

1. Descripción del problema

Ciertas tres plantas de carbón abastecen a 4 regiones, y se supone que la misma cantidad de carbón tiene el mismo efecto en estas regiones.La producción anual de cada planta de carbón, la demanda en cada región y la tarifa de flete unitario de cada planta de carbón a cada región son los siguientes: Mostrar, tratar de determinar el plan de implementación óptimo.

Lugar de venta\Origen	B1	B2	B3	B4	Rendir
A1	5	3	10	4	90
A2	2	6	9	6	40
A3	14	10	5	7	70
Ventas	30	50	100	40

2. Análisis de problemas

Suministro total=30+40+50=120

Demanda total=16+30+24+30=100

(1) Agregue un lugar de venta virtual E, de modo que la demanda total sea 120-100=20.

Por lo tanto, la nueva tabla de oferta y demanda y tarifa unitaria es la siguiente.

Lugar de venta\Origen	B	B	B3	B4	Rendir
A,	5	3	10	4	90
A2	2	6	9	6	40
A3	14	10	5	7	70
A4	0	0	0	0	20
Ventas	30	50	100	40	220

3. Resolución de problemas

Resolver usando python:

Aquí puede usar (método de aproximación de Vogel) para encontrar la solución factible básica inicial

'-----------------------------------Vogel法---------------------------------'
supplyNum = 4  # 供应商数量
demandNum = 4  # 需求商数量
A = np.array([90,40,70,20])  # 产量
B = np.array([30,50,100,40])  # 销量
C = np.array([[5,3,10,4], [2,6,9,6], [14,10,5,7],[0,0,0,0]])  # 成本
X = np.zeros((supplyNum, demandNum))  # 初始解
c = copy.deepcopy(C)
numPunish = [0] * (supplyNum + demandNum)  # 整体罚数


def pivot(X, A, B, C):
    # 求解罚数，其中列罚数排在行罚数后面
    for i in range(supplyNum):
        sortList = np.sort(C[i, :])
        numPunish[i] = sortList[1] - sortList[0]
    for i in range(demandNum):
        sortList = np.sort(C[:, i])
        numPunish[i + supplyNum] = sortList[1] - sortList[0]

    maxIndex = np.argmax(numPunish)  # 寻找最大罚数的索引

    # 若最大的罚数属于行罚数
    if maxIndex < supplyNum:
        minIndex = np.argmin(C[maxIndex, :])
        index = (maxIndex, minIndex)  # 得到最大罚数的一行中最小的运价
        # 若产量大于销量
        if A[maxIndex] > B[minIndex]:
            X[index] = B[minIndex]  # 更新解
            C[:, minIndex] = maxNumber  # 将已经满足的一列中的运价增大替代删除操作
            A[maxIndex] -= B[minIndex]  # 更新剩余产量
            B[minIndex] = 0  # 更新已经满足的销量
        # 若销量大于产量
        else:
            X[index] = A[maxIndex]
            C[maxIndex, :] = maxNumber
            B[minIndex] -= A[maxIndex]  # 更新销量
            A[maxIndex] = 0

    # 若最大的罚数为列罚数
    else:
        minIndex = np.argmin(C[:, maxIndex - supplyNum])  # 这时maxIndex-supplyNum是罚数最大的列
        index = (minIndex, maxIndex - supplyNum)
        if A[minIndex] > B[maxIndex - supplyNum]:  # 这里是产量大于销量，因此有限满足销量
            X[index] = B[maxIndex - supplyNum]
            C[:, maxIndex - supplyNum] = maxNumber
            A[minIndex] -= B[maxIndex - supplyNum]
            B[maxIndex - supplyNum] = 0
        else:
            X[index] = A[minIndex]
            C[minIndex, :] = maxNumber
            B[maxIndex - supplyNum] -= A[minIndex]
            A[minIndex] = 0
    return X, A, B, C


# 沃格尔法得到初始解
def Vogel(A, B, C):
    X = np.zeros((supplyNum, demandNum))  # 初始解
    numPunish = [0] * (supplyNum + demandNum)  # 整体罚数
    # 迭代，直到所有的产量和销量全部满足
    while (A != 0).any() and (B != 0).any():
        X, A, B, C = pivot(X, A, B, C)
    return X


# 上面对于条件的判断，还需要对销量和需求量进行改变
solutionVogel = Vogel(A, B, c)
print('Vogel法得到的初始解为：')
print(solutionVogel)
print('Vogel法得到的总运费为:', (C * solutionVogel).sum())

Resultado de salida:

Vogel法得到的初始解为：
[[ 0. 50.  0. 40.]
 [30.  0. 10.  0.]
 [ 0.  0. 70.  0.]
 [ 0.  0. 20.  0.]]
Vogel法得到的总运费为: 810.0

Los tres problemas de producción y ventas anteriores son comunes Además de los problemas de producción y ventas, también hay problemas de transporte de demanda elástica y problemas de transporte de transbordo intermedio.

No seré prolijo aquí, ¡verifique la información usted mismo!

3. Problemas de asignación

3.1 Modelo matemático del problema de asignación

Ejemplo 7 Se propone asignar $norte$ personas para realizar $norte$ un trabajo, y cada persona realizará un y solo un trabajo, si $i$ se asigna a la segunda persona para realizar el primer $j$ trabajo, tomará una $c_{ij}$ unidad de tiempo ¿Cómo se debe asignar el trabajo? minimizar el tiempo total empleado por los trabajadores?

Es fácil ver que para dar una instancia de un problema de asignación, solo es necesario dar la matriz $C=(c_{ij})$ , $C$ llamada matriz de coeficientes del problema de asignación. Introduce una variable que tome = 1 si el trabajo está $x_{ij}$ asignado y = 0 en caso contrario. El modelo matemático del problema de asignación anterior es: $i$ $j$ $x_{ij}$ $x_{ij}$

$\begin{alineado} &\min \sum_{i=1}^{n} \sum_{j=1}^{n} c_{ij} x_{ij} \\ &\text { st } \sum_{j =1}^{n} x_{ij}=1 \\ &\sum_{i=1}^{n} x_{ij}=1 \\ &x_{ij}=0 \text { o } 1 \end{ alineado}$

La solución factible del problema de asignación anterior se puede representar mediante una matriz, cada fila y cada columna tiene un y solo un elemento es 1, y los otros elementos son 0; se puede representar $1,...,n$ mediante una permutación de .

Las variables en el problema solo pueden tomar 0 o 1, que es un problema de programación 0-1. El problema general de programación 0-1 es extremadamente difícil de resolver. Sin embargo, el problema de asignación no es difícil de resolver.La matriz de coeficientes del sistema de ecuaciones de restricción es muy especial (llamada matriz de módulo unitario completo, y sus subfórmulas distintas de cero de todos los órdenes son ±1), y el componente de su no -La solución factible negativa solo puede tomar 0 o 1, por lo que la restricción $x_{ij}$ = 0 o 1 se puede reescribir como $x_{ij}$ ≥ 0 sin cambiar su solución. En este punto, el problema de asignación se transforma en un problema especial de transporte donde $m=n$ , $a_{i}=b_{j}=1$ .

3.2 El algoritmo húngaro para resolver el problema de asignación

El algoritmo se basa principalmente en el hecho de $C=(c_{ij})$ que $B=(b_{ij})$ un problema de asignación con C o B como matriz de coeficientes tiene la misma asignación óptima si se suma o resta el mismo número a cada elemento en una fila (o columna) de la matriz de coeficientes, lo que da como resultado una nueva matriz .

Ejemplo 8 Resolviendo el problema de asignación, la matriz de coeficientes es

$C=\left[\begin{matriz}{llll} 16&15&19&22\\17&21&19&18\\24&22&18&17\\17&19&22&16\end{matriz}\right]$

Solución de la tarea:

Resta 15 del elemento de la primera fila, el elemento más pequeño de esta fila, de manera similar, resta 17 del elemento de la segunda fila, resta 17 del elemento de la tercera fila y resta 16 del elemento de la última fila, obtenemos:

$B_{1}=\left[\begin{matriz}{llll} 1&0&4&7\\0&4&2&1\\7&5&1&0\\1&3&6&0 \end{matriz}\right]$

Luego resta 1 de cada uno de los elementos en la tercera columna para obtener

$B_{2}=\left[\begin{matriz}{cccc} 1 & 0^{*} & 3 & 7 \\ 0^{*} & 4 & 1 & 1 \\ 7 & 5 & 0^{* } & 0 \\ 1 & 3 & 5 & 0^{*} \end{matriz}\right]$

El problema de asignación con $B_{2}$ la matriz de coeficientes tiene una asignación óptima

$\left(\begin{matriz}{llll}1&2&3&4\\2&1&3&4\end{matriz}\right)$

Por equivalencia, también es una asignación óptima de C.

solución pitón:

from scipy.optimize import linear_sum_assignment
import numpy as np
cost = np.array([[16,15,19,22], [17,21,19,18], [24,22,18,17],[17,19,22,16]])
row_ind, col_ind = linear_sum_assignment(cost)
print('row_ind:', row_ind)  # 开销矩阵对应的行索引
print('col_ind:', col_ind)  # 对应行索引的最优指派的列索引
print('cost:', cost[row_ind, col_ind])  # 提取每个行索引的最优指派列索引所在的元素，形成数组
print('cost_sum:', cost[row_ind, col_ind].sum())  # 最小开销

Resultado de salida:

row_ind: [0 1 2 3]
col_ind: [1 0 2 3]
cost: [15 17 18 16]
cost_sum: 66

Ejemplo 9 Resolviendo el problema de asignación de la matriz de coeficientes C

$C=\left[\begin{array}{lllll} 12 & 7 & 9 & 7 & 9 \\ 8 & 9 & 6 & 6 & 6 \\ 7 & 17 & 12 & 14 & 12 \\ 15 & 14 & 6 y 6 y 10 \\ 4 y 10 y 7 y 10 y 6 \end{matriz}\right]$

implementación de pitón:

from scipy.optimize import linear_sum_assignment
import numpy as np
cost = np.array([[12, 7, 9 ,7, 9], 
                 [8, 9, 6, 6, 6], 
                 [7, 17, 12, 14, 12],
                 [15,14, 6 ,6, 10],
                 [4,10 ,7 ,10 ,6]])
row_ind, col_ind = linear_sum_assignment(cost)
print('row_ind:', row_ind)  # 开销矩阵对应的行索引
print('col_ind:', col_ind)  # 对应行索引的最优指派的列索引
print('cost:', cost[row_ind, col_ind])  # 提取每个行索引的最优指派列索引所在的元素，形成数组
print('cost_sum:', cost[row_ind, col_ind].sum())  # 最小开销

Resultado de salida:

row_ind: [0 1 2 3 4]
col_ind: [1 2 0 3 4]
cost: [7 6 7 6 6]
cost_sum: 32

4. Teoría de la dualidad y análisis de sensibilidad

4.1 Problemas primitivos y duales

Considere el siguiente par de modelos de programación lineal:

$\max c^{T} x \quad \text { st } \quad A x \leq b, x \geq 0$ (PAGS)

$\min b^{T} y \quad \text { st } \quad A^{T} y \geq c, y \geq 0$ (D)

Llame (P) el problema primal y (D) su problema dual.

Con menos rigor, el problema dual puede verse como una "transposición fila-columna" del problema original:

(1) Los coeficientes de la j-ésima columna en el problema original son los mismos que los coeficientes de la j-ésima fila en el problema dual;

(2) Cada fila de coeficientes de la función objetivo original es igual a cada columna constante en el lado derecho de su problema dual;

(3) Cada columna constante en el lado derecho del problema original es igual a cada fila de coeficientes de su función objetivo dual;

(4) En este par de problemas, la dirección de desigualdad y la dirección de optimización son opuestas.

Considere la programación lineal:

$\max c^{T} x \quad \text { st } \quad A x \leq b, x \geq 0$

Convirtiendo las restricciones de igualdad en restricciones de desigualdad, podemos obtener

$\min c^{T} x \quad \text { st }\left[\begin{array}{c} A \\ -A \end{array}\right] x \geq\left[\begin{array} {c} b \\ -b \end{matriz}\right], x \geq 0$

Su doble problema es

$\max \left[\begin{array}{ll} b^{T} & -b^{T} \end{array}\right]\left[\begin{array}{l} y_{1} \\ y_{2} \end{matriz}\right] \quad \text { st }\left[\begin{matriz}{ll} A^{T} & -A^{T} \end{matriz}\right] \left[\begin{matriz}{l} y_{1} \\ y_{2} \end{matriz}\right] \leq c$

donde $y_{1}$ y representan los grupos de variables duales correspondientes a la suma $y_{2}$ de restricciones , respectivamente. , entonces la fórmula anterior se puede escribir como $Ah \ geq b$ $-Ax\geq -b$ $y=y_{1}-y_{2}$

$\min b^{T} y \quad \text { st } \quad A^{T} y \geq c, y \geq 0$

La relación entre el problema primal y las restricciones duales del dual:

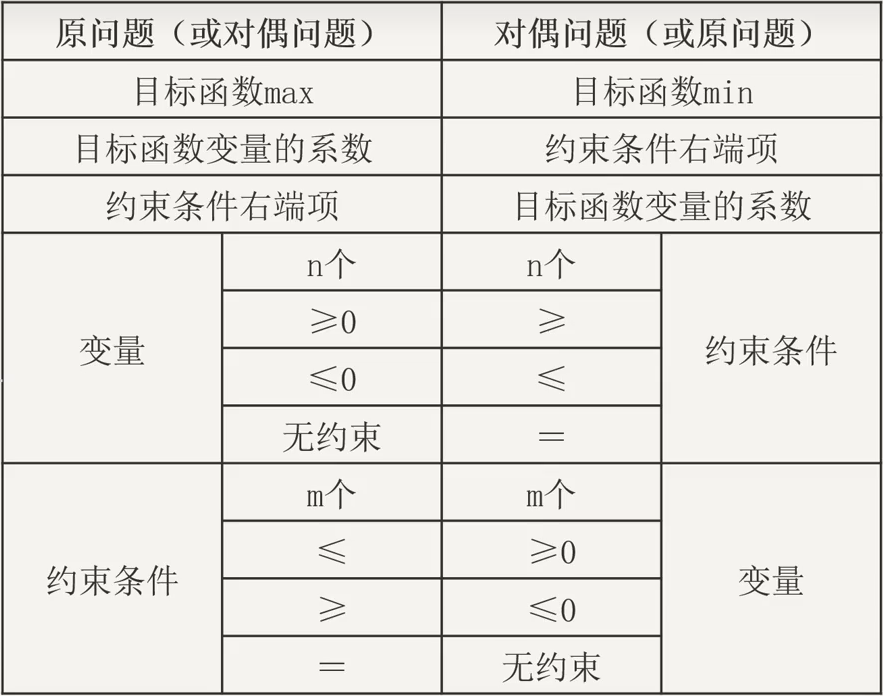
La formula:

El signo de desigualdad está en la misma dirección: el signo de desigualdad de la variable Max está en la misma dirección que el signo de desigualdad de la restricción min

La dirección del signo de desigualdad es opuesta: El signo de desigualdad de la restricción Max es opuesto al signo de desigualdad de la variable Min. El signo igual no corresponde a ninguna restricción:

El "=" de la condición de restricción corresponde a la variable "sin restricciones"

Ejemplo 1:

Intenta resolver el problema dual de la siguiente programación lineal.

$\begin{alineado} &\min Z=2 x_{1}+3 x_{2}-5 x_{3}+x_{4} \\ &\left\{\begin{matriz}{l} x_{1 }+x_{2}-3 x_{3}+x_{4} \geq 5 \\ 2 x_{1}+2 x_{3}-x_{4} \leq 4 \\ x_{2}+x_{ 3}+x_{4}=6 \\ x_{1} \leq 0 ; x_{2}, x_{3} \geq 0 ; x_{4} \epsilon R\end{matriz}\right. \end{alineado}$

Solución: Sean las variables duales correspondientes a las tres restricciones y1, y2 e y3 respectivamente, entonces el problema dual del problema original es:
$\begin{aligned} &\max Z^{\prime}=5 y_{1}+4 y_{2}+6 y_{3} \\ &\left\{\begin{array}{l} y_{1}+2 y_{2} \geq 2 \\ y_{1}+y_{3} \leq 3 \\ -3 y_{1}+2 y_{2}+y_{3} \leq-5 \\ y_{1}-y_{2}+y_{3}=1 \\ y_{1} \geq 0 ; y_{2} \leq 0 ; y_{3} \epsilon R \end{array}\right. \end{aligned}$

4.2 Propiedades básicas de los problemas duales

Los problemas primal y dual:

$\begin {array}{ll} \max Z=CX & \min Z^{\prime}=Y b \\ \begin{cases}AX \leq b \\ X \geq 0\end{cases} & \left \{\begin{matriz}{l} YA \geq C \\ Y \geq 0 \end{matriz}\right. \end{matriz}$

(1) Simetría
El dual del problema dual es el problema original
(2) Dualidad débil
Si $\overline{X}$ la solución factible del problema original (max) es una solución factible $\overline{Y}$ del problema dual (min), entonces $C\overline{X}\leq \overline{Y}b$ , demuestre:

problema max: $A\overline{X}\leq b$ multiplicacion por la izquierda $\overline{Y}$ $\overline{Y}A\overline{X}\leq \overline{Y}b$

problema mínimo: $\overline{Y}A\geq C$ multiplicación correcta $\overline{X}$ $\overline{Y}A\overline{X}\geq C\overline{X}$

(3) Ilimitado
Si el problema original (problema dual) tiene una solución ilimitada, entonces su problema dual (problema original) no tiene solución factible

(4) Optimalidad
Sea $\widehat{X}$ la solución factible del problema original y la solución factible $\widehat{Y}$ del problema dual, cuando $C\widehat{X}=\widehat{Y}b$ = , $\sombrero ancho{X},\sombrero ancho{Y}$ es la solución óptima

(5) Teorema de la dualidad
Si el problema original tiene una solución óptima, entonces el problema dual también tiene una solución óptima y los valores de la función escalar diaria son iguales

(6) Holgura complementaria
Sean $\sombrero ancho{X},\sombrero ancho{Y}$ las soluciones factibles del problema primal y del problema dual, respectivamente, y las soluciones factibles $X_{s},Y_{s}$ de sus variables de holgura, respectivamente, entonces $\sombrero ancho{X},\sombrero ancho{Y}$ la solución óptima es la solución óptima si y sólo si $Y_{s}\widehat{X}=0$ y $X_{s}\widehat{Y}=0$

Ejemplo 10 Problema conocido de programación lineal:

Se sabe que la solución óptima a su problema dual es $y_ {1} ^ {*} = \ fracción {4} {5}, y_ {2} ^ {*} = \ fracción {3} {5}, z = 5$ . Probar la teoría de la dualidad para encontrar la solución óptima del problema original

La solución es escribir primero su problema dual.

$\begin{aligned} &\max z=4 y_{1}+3 y_{2} \\ &\left\{\begin{array}{l} y_{1}+2 y_{2} \leq 2 \\ y_{1}-y_{2} \leq 3 \\ 2 y_{1}+3 y_{2} \leq 5 \\ y_{1}+y_{2} \leq 2 \\ 3 y_{1}+y_{2} \leq 3 \\ y_{1}, y_{2} \geq 0 \end{array}\right. \end{aligned}$ Agregar variables de holgura $\left\{\begin{array}{l} y_{1}+2 y_{2}+y_{s_{1}}=2 \\ y_{1}-y_{2}+y_{s_{2}}=3 \\ 2 y_{1}+3 y_{2}+y_{s_{3}}=5 \\ y_{1}+y_{2}+y_{s_{4}}=2 \\ 3 y_{1}+y_{2}+y_{s_{5}}=3 \\ y_{1}, y_{2}, y_{s_{1}}, y_{s_{2}}, y_{s_{3}}, y_{s_{4}}, y_{s_{5}} \geq 0 \end{array}\right.$ a la solución óptima

$\left\{\begin{matriz}{l} y_{s_{1}}=0 \\ y_{s_{2}} \neq 0 \\ y_{s_{3}} \neq 0 \\ y_{s_ {4}} \neq 0 \\y_{s_{5}}=0 \end{matriz}\right.$ $\left\{\begin{matriz}{l} y_{s_{2}} x_{2}^{*}=0 \\ y_{s_{3}} x_{3}^{*}=0 \\ y_{s_{4}} x_{4}^{*}=0 \end{matriz}\right.$ Solución de Relajación Complementaria $\left\{\begin{matriz}{l} x_{2}^{*}=0 \\ x_{3}^{*}=0 \\ x_{4}^{*}=0 \end{matriz }\Correcto.$

Vuelva a analizar el problema original:
$\left\{\begin{matriz}{l} x_{1}+x_{2}+2 x_{3}+x_{4}+3 x_{5}-x_{s_{1}}=4 \\ 2 x_{1}-x_{2}+3 x_{3}+x_{4}+x_{5}-x_{s_{2}}=3 \\ x_{1}, x_{2}, x_{ 3}, x_{4}, x_{5}, x_{s_{1}}, x_{s_{2}} \geq 0 \end{matriz}\right.$ dado que $y_{1}^{*} \neq 0, y_{2}^{*} \neq 0$ $\left\{\begin{matriz}{l} x_{s_{1}}=0 \\ x_{s_{2}}=0 \end{matriz}\right.$ el

$x_{s_{1}}, x_{s_{2}}, x_{2}^{*}, x_{3}^{*}, x_{4}^{*}$ Sustituya la $\left\{\begin{matriz}{l} x_{1}^{*}+3 x_{5}^{*}=4 \\ 2 x_{1}^{*}+x_{5}^{ *}=3 \end{matriz}\right.$ solución para obtener la $\left\{\begin{matriz}{l} x_{1}^{*}=1 \\ x_{5}^{*}=1 \end{matriz}\right.$ solución óptima : $\begin{alineado} &X^{*}=(1,0,0,0,1)^{T} \\ &\omega^{*}=5 \end{alineado}$

4.3 Análisis de sensibilidad

Se plantean dos interrogantes: cuando uno o más de estos coeficientes cambien, ¿qué pasará con la solución óptima del problema de programación lineal que se ha obtenido?, o cuando cambien estos coeficientes, ¿cuál es la solución óptima del problema de programación lineal? o la base óptima no cambia. No lo discutiremos aquí.

4.4 Programación lineal paramétrica

La programación lineal paramétrica consiste en estudiar $a_{ij},b_{i},c_{j}$ el valor de cada punto crítico en el que cambia la solución óptima cuando uno de estos parámetros cambia continuamente. Es decir, se usa un parámetro como parámetro, y la función objetivo es una función lineal de este parámetro en un cierto intervalo, y la condición de restricción que contiene este parámetro es una ecuación lineal o una desigualdad. Por lo tanto, el método símplex y el método símplex dual todavía pueden usarse para analizar el problema de programación lineal paramétrica.

4.4.1 Método símplex:

Ejemplo: Resolver un problema de programación lineal utilizando el método Simplex
$\begin{alineado} &\max z=2 x_{1}+x_{3} \\ &\text { st }\left\{\begin{array}{c} 5 x_{2} \leq 15 \\ 6 x_{1}+2 x_{2} \leq 24 \\ x_{1}+x_{2} \leq 5 \\ x_{1}, x_{2} \geq 0 \end{matriz}\right. \end{alineado}$

(1) Estandarización

$\begin{alineado} &\max z=2 x_{1}+x_{2}+0 x_{3}+0 x_{4}+0 x_{5} \\ &\text { st }\left\{ \begin{matriz}{c} 5 x_{2}+x_{3}=15 \\ 6 x_{1}+2 x_{2}+x_{4}=24 \\ x_{1}+x_{2 }+x_{5}=5 \\ x_{1}, x_{2}, x_{3}, x_{4}, x_{5} \geq 0 \end{matriz}\right. \end{alineado}$

(2) Use la programación de python:

import numpy as np
class Simplex:
    def __init__(self) -> None:
        self.solutionStatus = 0

    def set_param(self, A, b, c, baseInd):

        self.A = A
        self.m, self.n = self.A.shape
        self.b = b
        self.c = c
        self.baseInd = baseInd
        self.nonbaseInd = [i for i in range(self.n) if i not in self.baseInd]
        self.B = self.A[:, self.baseInd]
        self.N = self.A[:, self.nonbaseInd]
        self.B_inv = self.B.I

    def main(self):
        # 计算非基变量的检验数，基变量检验数为0
        reducedCost = [0] * self.n
        X_B = None
        simplexTable = SimplexTable()
        while (self.solutionStatus == 0):
            for i in range(self.n):
                reducedCost[i] = float(self.c[:, i] - np.dot(self.c[:, self.baseInd], self.A[:, i]))
                # p_j已经全部左乘B_inv，因此这里c_B可以直接与更新后的p_j相乘
            self.solutionStatus = self.check_solutionStatus(reducedCost)
            simplexTable.show(self.A, self.b, self.c, reducedCost, self.baseInd, self.solutionStatus)
            if self.solutionStatus == 0:
                inVarInd = reducedCost.index(max(reducedCost))
                outVarInd = self.get_outVar(inVarInd)
                self.baseInd[self.baseInd.index(outVarInd)] = inVarInd
                self.nonbaseInd[self.nonbaseInd.index(inVarInd)] = outVarInd
                # 得到新基
                self.B = self.A[:, self.baseInd]
                self.B_inv = self.B.I
                self.b = np.dot(self.B_inv, self.b)
                X_B = self.b.T.tolist()[0]
                self.A[:, inVarInd] = self.A[:, outVarInd]
                self.A[:, self.nonbaseInd] = np.dot(self.B_inv, self.A[:, self.nonbaseInd])
            else:
                break
        if self.solutionStatus == 1:
            solution = {}
            for i in range(self.n):
                if i in self.baseInd:
                    solution[i] = X_B[self.baseInd.index(i)]
                if i in self.nonbaseInd:
                    solution[i] = 0
            objctive = float(np.dot(np.dot(self.c[:, self.baseInd], self.B_inv), self.b))

            return solution, objctive, self.solutionStatus
        else:
            solution = None
            objctive = None
            return solution, objctive, self.solutionStatus

    def check_solutionStatus(self, reducedCost):
        if all(x < 0 or x == 0 for x in reducedCost):
            # 所有检验数<=0
            if any(reducedCost[i] == 0 for i in self.nonbaseInd):
                # 存在非基变量的检验数为0
                return 2  # 无穷多最优解
            else:
                return 1  # 唯一最优解
        else:
            if all(all(x < 0 for x in self.A[:, i]) for i in self.nonbaseInd if reducedCost[i] > 0):
                return 3  # 无界解
            else:
                # 选择最大检验数对应的非基变量入基
                return 0

    def get_outVar(self, inVarInd):
        inVarCoef = self.A[:, inVarInd]
        ratio = [np.inf] * self.m
        for i in range(len(inVarCoef)):
            if float(inVarCoef[i, :]) > 0:
                ratio[i] = float(self.b[i, :]) / float(inVarCoef[i, :])
        outVarInd = self.baseInd[ratio.index(min(ratio))]
        return outVarInd

class SimplexTable:
    def __init__(self):
        # 左端表头格式设置
        self.setting_left = '{:^8}'+'{:^8}'+'{:^8}|'
        # 右端变量格式设置
        self.setting_var = '{:^8}|'
        # 求解状态格式设置
        self.setting_status = '{:^24}|'+'{:^44}|'
    def show(self,A,b,c,reducedCost,baseInd,solutionStatus):
        var_num = A.shape[1]
        # 打印系数行
        c_j_list = c.flatten().tolist()[0]
        print('='*80)
        print(self.setting_left.format('','c_j',''),end = '')
        for i in c_j_list:
            print(self.setting_var.format(i),end = '')
        print()
        # 打印变量行
        print(self.setting_left.format('c_B','x_B','b'),end = '')
        for i in range(var_num):
            print(self.setting_var.format('x'+str(i)),end = '')
        print()
        # 打印变量与矩阵
        for i in range(len(baseInd)):
            varInd = baseInd[i]
            varCeof = round(float(c[:,varInd]),2)
            varValue = round(float(b[i,:]),2)
            row = A[i,:].flatten().tolist()[0]
            print(self.setting_left.format(str(varCeof),'x'+str(varInd),str(varValue)),end='')
            for i in range(var_num):
                print(self.setting_var.format(round(row[i],2)),end = '')
            print()
        # 打印检验数
        print(self.setting_left.format('','c_j-z_j',''),end='')
        for i in reducedCost:
            print(self.setting_var.format(round(i,2)),end = '')
        print()
        # 显示求解状态
        if solutionStatus == 0:
            print(self.setting_status.format('status','...Iteration continues...'))
        if solutionStatus == 1:
            print(self.setting_status.format('status','Unique Optimal Solution'))
            B = A[:,baseInd]
            B_inv =  B.I
            objctive = float(np.dot(np.dot(c[:, baseInd], B_inv), b))
            print(self.setting_status.format('objctive', round(objctive,2)))
            solution = [0]*var_num
            X_B = b.T.tolist()[0]
            for i in range(var_num):
                if i in baseInd:
                    solution[i] = X_B[baseInd.index(i)]
            print(self.setting_left.format('', 'solution', ''), end='')
            for i in solution:
                print(self.setting_var.format(round(i, 2)), end='')
            print()

        if solutionStatus == 2:
            print(self.setting_status.format('status','Multiple Optimal Solutions'))
            B = A[:, baseInd]
            B_inv = B.I
            objctive = float(np.dot(np.dot(c[:, baseInd], B_inv), b))
            print(self.setting_status.format('objctive', round(objctive, 2)))
        if solutionStatus == 3:
            print(self.setting_status.format('status','Unboundedness'))

'''=============================================================================='''
A = np.matrix([[0,5,1,0,0],
               [6,2,0,1,0],
               [1,1,0,0,1]], dtype=np.float64)
                    # 必须设置精度，否则在替换矩阵列时会被自动圆整
b = np.matrix([[15], [24], [5]], dtype=np.float64)
c = np.matrix([2,1,0,0,0], dtype=np.float64)
baseInd = [2,3,4]

s=Simplex()
s.set_param( A, b, c, baseInd)
s.main()

Resuelva la lista de esta forma, que satisface las condiciones básicas del método símplex, como sigue:

================================================================================
          c_j           |  2.0   |  1.0   |  0.0   |  0.0   |  0.0   |
  c_B     x_B      b    |   x0   |   x1   |   x2   |   x3   |   x4   |
  0.0      x2     15.0  |  0.0   |  5.0   |  1.0   |  0.0   |  0.0   |
  0.0      x3     24.0  |  6.0   |  2.0   |  0.0   |  1.0   |  0.0   |
  0.0      x4     5.0   |  1.0   |  1.0   |  0.0   |  0.0   |  1.0   |
        c_j-z_j         |  2.0   |  1.0   |  0.0   |  0.0   |  0.0   |
         status         |         ...Iteration continues...          |
================================================================================
          c_j           |  2.0   |  1.0   |  0.0   |  0.0   |  0.0   |
  c_B     x_B      b    |   x0   |   x1   |   x2   |   x3   |   x4   |
  0.0      x2     15.0  |  0.0   |  5.0   |  1.0   |  0.0   |  0.0   |
  2.0      x0     4.0   |  1.0   |  0.33  |  0.0   |  0.17  |  0.0   |
  0.0      x4     1.0   |  0.0   |  0.67  |  0.0   | -0.17  |  1.0   |
        c_j-z_j         |  0.0   |  0.33  |  0.0   | -0.33  |  0.0   |
         status         |         ...Iteration continues...          |
================================================================================
          c_j           |  2.0   |  1.0   |  0.0   |  0.0   |  0.0   |
  c_B     x_B      b    |   x0   |   x1   |   x2   |   x3   |   x4   |
  0.0      x2     7.5   |  0.0   |  0.0   |  1.0   |  1.25  |  -7.5  |
  2.0      x0     3.5   |  1.0   |  0.0   |  0.0   |  0.25  |  -0.5  |
  1.0      x1     1.5   |  0.0   |  1.0   |  0.0   | -0.25  |  1.5   |
        c_j-z_j         |  0.0   |  0.0   |  0.0   | -0.25  |  -0.5  |
         status         |          Unique Optimal Solution           |
        objctive        |                    8.5                     |
        solution        |  3.5   |  1.5   |  7.5   |   0    |   0    |

Solucion optima: ${X}^{*}=(3.5,1.5,7.5,0,0)^{T}$

El valor óptimo: $z^{*} = 8,5$

Más discusión sobre el método simplex:

1. Método de variables artificiales (método de la gran M)

Después de que algunos problemas de programación lineal se transforman en forma canónica, no hay una matriz de identidad en la matriz de coeficientes de restricción, por lo que es necesario agregar variables artificiales a las restricciones para construir un nuevo problema de programación lineal. Llevar el coeficiente de la variable artificial en la función objetivo a un número negativo arbitrariamente grande puede evitar que la variable artificial aparezca en la solución óptima durante el proceso de solución. Si todos los números de prueba en la tabla símplex final son menores o iguales a cero, pero todavía hay variables artificiales que no son cero en las variables base, el problema no está resuelto. A continuación, se dan los pasos de cálculo del método de la variable artificial.

2. Método de dos etapas

Utilice el método de la gran M para tratar con variables artificiales. Al resolver con una computadora electrónica, solo se puede ingresar en la computadora un número de la longitud máxima de palabra de la máquina para M. Si el valor del parámetro en el problema de programación lineal está cerca del número que representa M, o es mucho más pequeño que este número, el resultado del cálculo puede ser incorrecto debido al error en el valor de la computadora durante el cálculo.

Para superar esta dificultad, el problema de programación lineal después de agregar variables artificiales se puede calcular en dos etapas, lo que se denomina método de dos etapas.

Más información: Operations Research Edición n.° 16 | Combinación de puntos de conocimiento básico de programación lineal - método simplex - Zhihu

4.4.2 Método Simplex Dual:

Ejemplo: Resuelva PL usando el método dual simplex:

$\begin{alineado} &\operatorname{Min} W=2 x_{1}+3 x_{2}+4 x_{3} \\ &\text { st }\left\{\begin{array}{c} x_{1}+2 x_{2}+x_{3} \geq 3 \\ 2 x_{1}-x_{2}+3 x_{3} \geq 4 \\ x_{1}, x_{2} , x_{3} \geq 0 \end{matriz}\right. \end{alineado}$

(1) Estandarización:

$\begin{alineado} &\operatorname{Máx.} z=-2 x_{1}-3 x_{2}-4 x_{3} \\ &\text { st }\left\{\begin{array}{c } x_{1}+2 x_{2}+x_{3}-x_{4}=3 \\ 2 x_{1}-x_{2}+3 x_{3}-x_{5}=4 \\ x_{1}, x_{2}, x_{3}, x_{4}, x_{5} \geq 0 \end{matriz}\right. \end{alineado}$

Multiplicando ambos lados de las dos restricciones de igualdad por -1, obtenemos

$\begin{alineado} &\operatorname{Max}z=-2 x_{1}-3 x_{2}-4 x_{3} \\ &\text { st }\left\{\begin{array}{c } -x_{1}-2 x_{2}-x_{3}+x_{4}=-3 \\ -2 x_{1}+x_{2}-3 x_{3}+x_{5}= -4 \\ x_{1}, x_{2}, x_{3}, x_{4}, x_{5} \geq 0 \end{matriz}\right. \end{alineado}$

(2) Use la programación de python:

import re
import pandas as pd
from fractions import Fraction

# data = pd.read_csv("data2.csv", header=0, index_col=0)
# data=pd.DataFrame({"x1":[-2,-2,-1,-9],"x2":[-2,-3,-1,-12],"x3":[-1,-1,-5,-15],"x4":[1,0,0,0],"x5":[0,1,0,0],"x6":[0,0,1,0],"b":[-10,-12,-14,0]},index = ['x4', 'x5', 'x6',"sigma"])
data=pd.DataFrame({"x1":[-1,-2,-2],"x2":[-2,1,-3],"x3":[-1,-3,-4],"x4":[1,0,0],"x5":[0,1,0],"b":[-3,-4,0]},index = ['x4', 'x5' ,"sigma"])
print("=======原始表=======")

print(data)


def do_it(data):
    in_base_index = data.loc["sigma", :][data.loc['sigma', :] < 0].index
    rec = {}
    res_val = []
    for i in in_base_index:
        out_base_index = data.loc[:, i][data.loc[:, i] < 0].index.drop("sigma")
        for j in out_base_index:
            res = Fraction(data.loc["sigma", i], data.loc[j, i])
            res_val.append(res)
            rec[str(j) + "," + str(i)] = res

    def get_key(dic, value):
        return [k for k, v in dic.items() if v == value]

    s = get_key(rec, min(res_val))
    s = re.split(r"\,", s[0])

    # 这里是将本身变成1
    param1 = Fraction(1, data.loc[s[0], s[1]])
    data.loc[s[0], :] = data.loc[s[0], :] * param1
    # 将其他变为0
    for row in data.index.drop(s[0]):
        target = data.loc[row, s[1]]
        param2 = Fraction(-target, 1)
        data.loc[row, :] = data.loc[s[0], :] * param2 + data.loc[row, :]

    data = data.rename(index={s[0]: s[1]})
    print("================================")
    print(data)
    if (data["b"].drop("sigma") < 0).any():
        print("需要继续迭代！")
        do_it(data)
    else:
        print("迭代结束！")
    return data


# 如何b中的任何一个数小于零，都需要进一步操作
if (data["b"].drop("sigma") < 0).any():
    print("需要继续迭代！")
    do_it(data)
else:
    print("迭代结束！")

Resuelva la lista de esta forma, que satisface las condiciones básicas del método símplex dual, como sigue:

=======原始表=======
       x1  x2  x3  x4  x5  b
x4     -1  -2  -1   1   0 -3
x5     -2   1  -3   0   1 -4
sigma  -2  -3  -4   0   0  0
需要继续迭代！
================================
      x1    x2   x3 x4    x5   b
x4     0  -5/2  1/2  1  -1/2  -1
x1     1  -1/2  3/2  0  -1/2   2
sigma  0    -4   -1  0    -1   4
需要继续迭代！
================================
      x1 x2    x3    x4    x5     b
x2     0  1  -1/5  -2/5   1/5   2/5
x1     1  0   7/5  -1/5  -2/5  11/5
sigma  0  0  -9/5  -8/5  -1/5  28/5
迭代结束！

Solucion optima: ${X}^{*}=(11 / 5,2 / 5,0,0,0) ^{T}$

El valor óptimo: $\begin{alineado} &\nombre del operador{minW}=-\max { }^{*}= -[11 / 5 \times(-2)+2 / 5 \times(-3)]=28 / 5 \end {alineado}$

Modelado matemático de Python - Programación lineal

1. Programación lineal

1.1 Ejemplos y definiciones de programación lineal

1.2 Use la biblioteca scipy en Python para resolver el problema de programación lineal de la columna 1:

Análisis de parámetros de entrada:

Análisis de parámetros de salida:

2. Problemas de transporte

2.1 Modelado matemático del proceso de producción y balance de ventas:

2.2 El problema del transporte de la producción y el balance de ventas

2.3 El problema del transporte donde la producción supera las ventas

2.4 El problema del transporte que la producción es menor que las ventas

3. Problemas de asignación

3.1 Modelo matemático del problema de asignación

3.2 El algoritmo húngaro para resolver el problema de asignación

4. Teoría de la dualidad y análisis de sensibilidad

4.1 Problemas primitivos y duales

4.2 Propiedades básicas de los problemas duales

4.3 Análisis de sensibilidad

4.4 Programación lineal paramétrica

4.4.1 Método símplex:

4.4.2 Método Simplex Dual:

Supongo que te gusta