Teoría de grafos del modelado matemático

1 Conceptos básicos de gráficas

Una gráfica en teoría de grafos es una gráfica compuesta por un número de puntos dados y una línea que conecta los dos puntos. Esta gráfica se usa generalmente para describir una relación específica entre ciertas cosas. Los puntos se usan para representar cosas y una línea que conecta dos puntos. Indica que existe una relación entre las dos cosas correspondientes.

Una gráfica se puede describir en lenguaje matemático como: G(V(G),E(G)). V(vertex)Se refiere al conjunto de vértices del gráfico E(edge)y se refiere al conjunto de aristas del gráfico.

Dependiendo de si las aristas tienen dirección, los gráficos se pueden dividir en gráficos no dirigidos y gráficos dirigidos . Además, algunos gráficos pueden tener pesos en sus bordes y dichos gráficos se denominan gráficos ponderados .

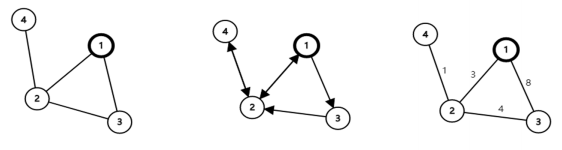
2 Cómo hacer fotos

2.1 Dibujar directamente

URL de la herramienta de dibujo en línea

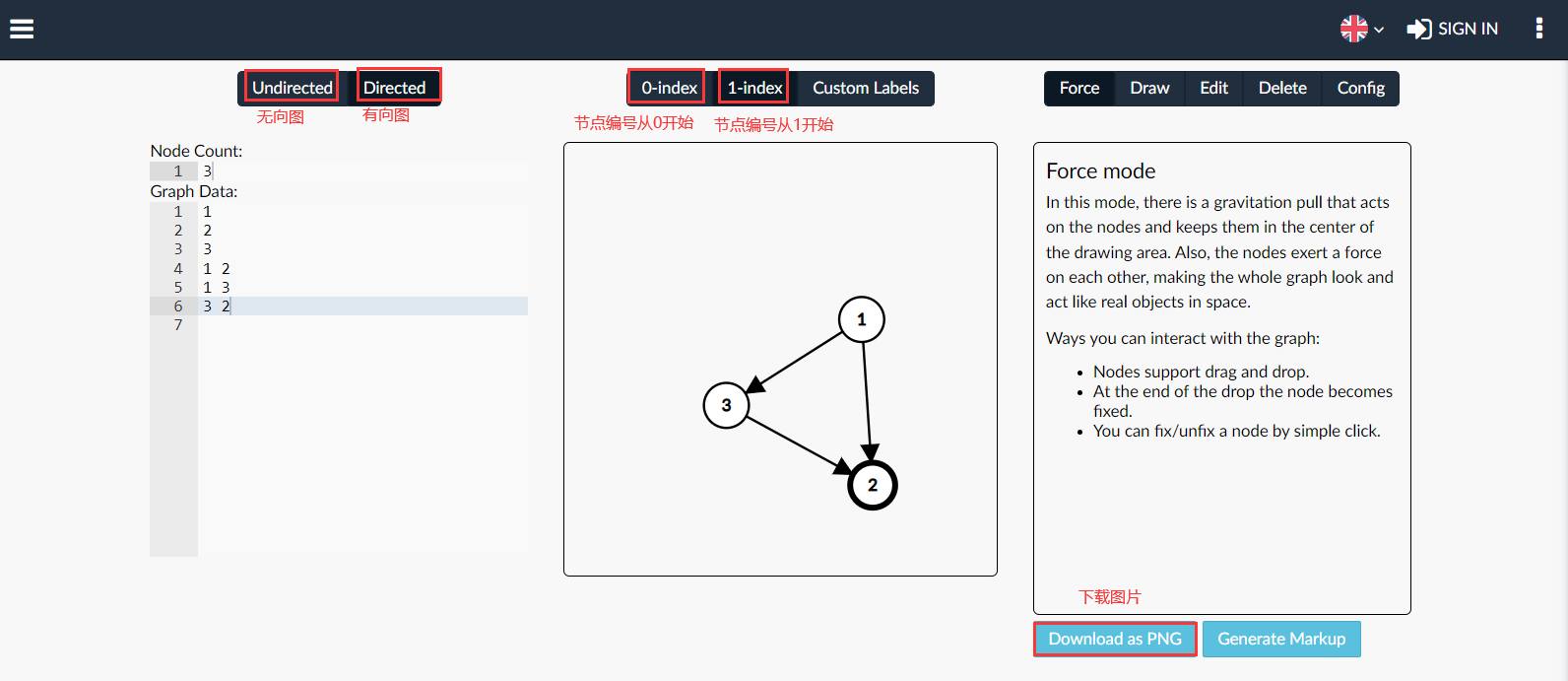
2.2 Programación y dibujo

Gráfico no dirigido

• graph(s,t): puede crear bordes entre los nodos correspondientes en sy generar un gráficot
• graph(s,t,w): Se puede crear un borde entre los nodos correspondientes en sy con un peso y generar un gráfico.tw

Para hacer un gráfico dirigido, simplemente graphcambie digrapha .

1️⃣ Gráfico no dirigido

% 无权重，也可以说每条边的权重默认为1
s1 = [1,2,3,4];
t1 = [2,3,1,1];
% 函数graph(s,t)：可在 s 和 t 中的对应节点之间创建边，并生成一个图
% s 和 t 都必须具有相同的元素数；这些节点必须都是从1开始的正整数，或都是字符串元胞数组。
G1 = graph(s1, t1);
plot(G1)

% 注意字符串元胞数组是用大括号包起来的哦
s2 = {
    
    '学校','电影院','网吧','酒店'};
t2 = {
    
    '电影院','酒店','酒店','KTV'};
G2 = graph(s2, t2);
plot(G2, 'linewidth', 2)  % 设置线的宽度
% 下面的命令是在画图后不显示坐标
set( gca, 'XTick', [], 'YTick', [] );  

% 有权重
s = [1,2,3,4];
t = [2,3,1,1];
w = [3,8,9,2];
% 函数graph(s,t,w)：可在 s 和 t 中的对应节点之间以w的权重创建边，并生成一个图
G = graph(s, t, w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
set( gca, 'XTick', [], 'YTick', [] );  

❗️Nota:

• Tenga en cuenta que los números solo se pueden numerar consecutivamente a partir de 1 (de lo contrario, se informará un error). No defina los números casualmente, porque la numeración predeterminada es consecutiva y es posible no escribirla.

s = [1,2,3,50];
t = [2,3,1,1];
G = graph(s, t);
plot(G)

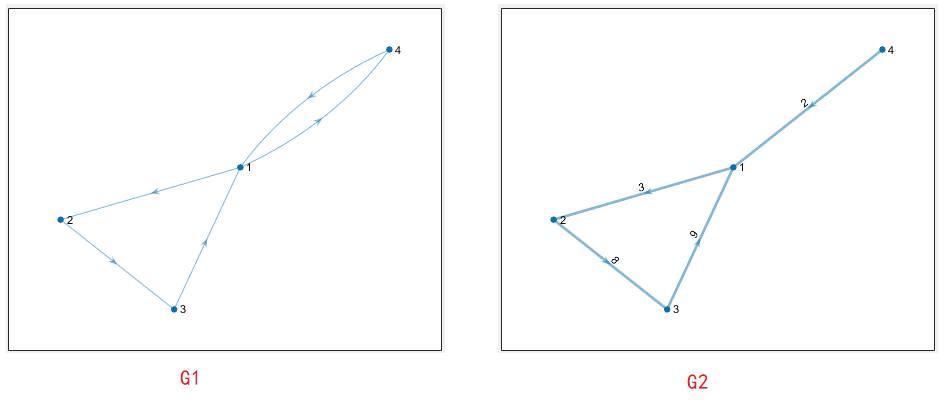
2️⃣ Gráfico dirigido

% 无权图 digraph(s,t)
s = [1,2,3,4,1];
t = [2,3,1,1,4];
G1 = digraph(s, t);
plot(G1)
set( gca, 'XTick', [], 'YTick', [] );  

% 有权图 digraph(s,t,w)
s = [1,2,3,4];
t = [2,3,1,1];
w = [3,8,9,2];
G2 = digraph(s, t, w);
plot(G2, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
set( gca, 'XTick', [], 'YTick', [] );  

☀️ Resumen:

• Los gráficos producidos por Matlab no son muy hermosos, si hay relativamente pocos nodos, se recomienda usarlos en línea.

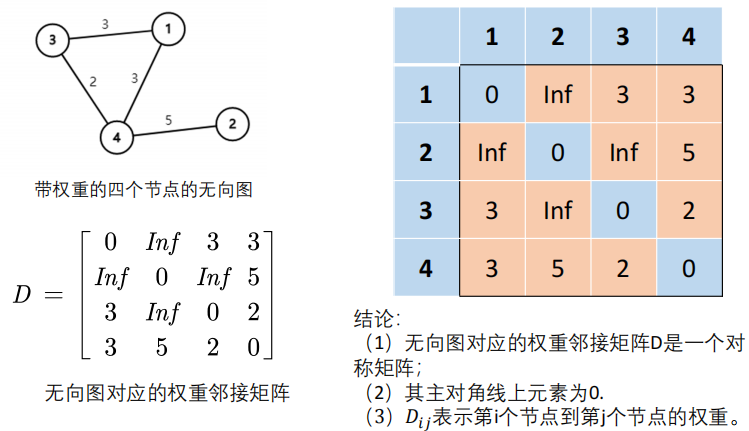
3 Matriz de adyacencia ponderada

3.1 Gráfico no dirigido

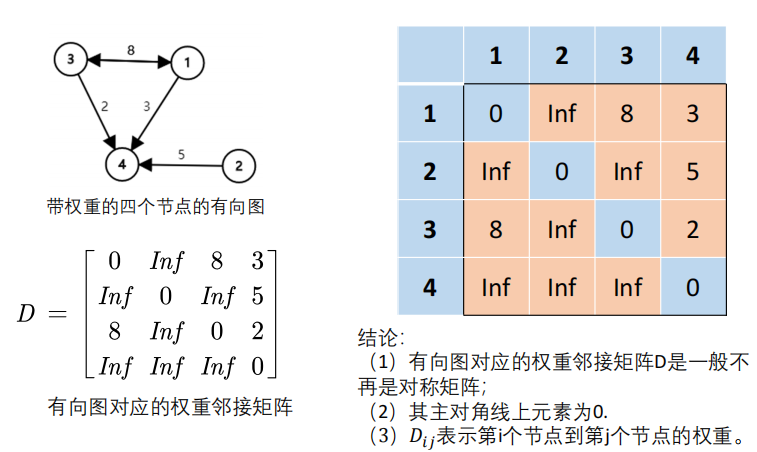
3.2 Gráfico dirigido

4 algoritmo de Dijkstra

4.1 Descripción general del algoritmo

Hay un total de nueve ubicaciones del 0 al 8 en la imagen. Si las ubicaciones están conectadas por una línea recta, significa que se puede llegar a los dos lugares directamente. El valor al lado de la línea recta indica la distancia entre los dos lugares .

El punto inicial es 0 y el punto final es 4. ¿Cómo tomar la distancia más corta?

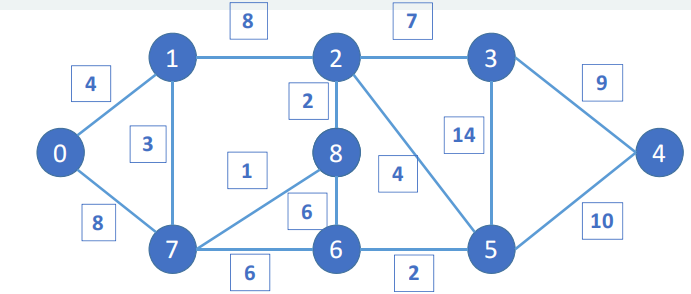
Utilice Dijkstraalgoritmos para resolver los problemas anteriores.

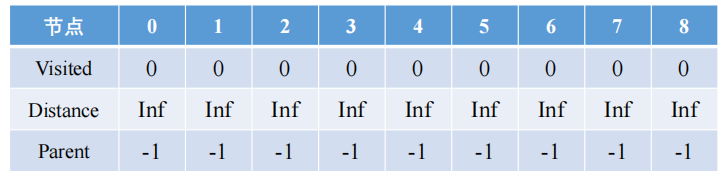
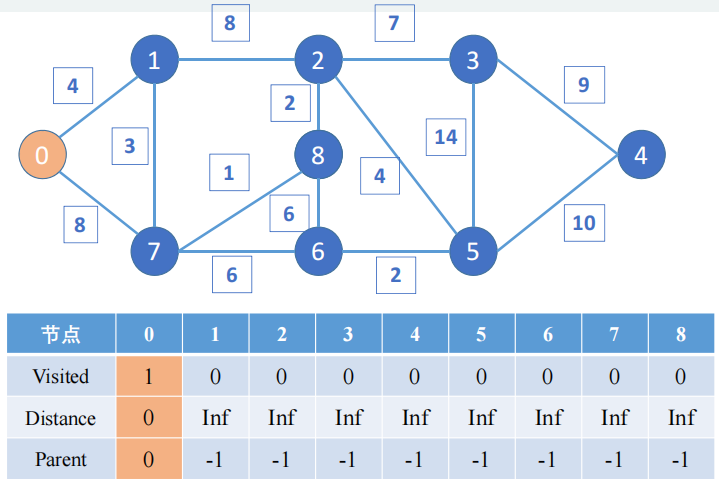
1️⃣ Inicialización

Visited: Todos los nodos no están visitados;
Distance: La distancia entre todos los nodos es Inf;
Parent: El nodo principal (nodo anterior) de todos los nodos es -1, lo que indica que no existe

1️⃣ El punto de partida es 0, actualiza la tabla:

• El estado de acceso del nodo 0 cambia a 1
• La distancia correspondiente al nodo 0 se convierte en 0
• El nodo padre del nodo 0 está representado por 0. Por supuesto, puede representarse mediante otros símbolos.

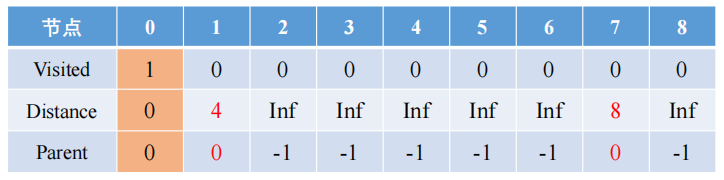
2️⃣ Actualice la información del nodo (B) adyacente al nodo 0 (A). Tenga en cuenta que el nodo B aquí no se visita.

• Si la distancia entre A y B + la distancia entre A es menor que la distancia entre B, entonces actualizamos la distancia entre B a una distancia menor, actualizamos el nodo principal de B a A e incluimos los nodos con una distancia menor en el nodo visitado

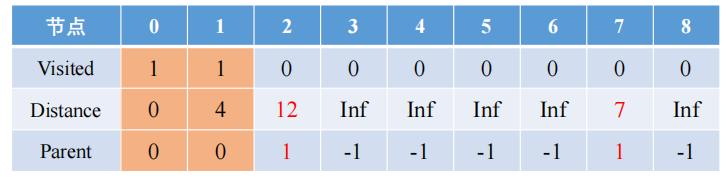
3️⃣ Actualice la información del nodo (B) adyacente al nodo 1 (A). Tenga en cuenta que el nodo B aquí no se visita.

• Si la distancia entre A y B + la distancia entre A es menor que la distancia entre B, entonces actualizamos la distancia entre B a una distancia menor, actualizamos el nodo principal de B a A e incluimos los nodos con una distancia menor en el nodo visitado

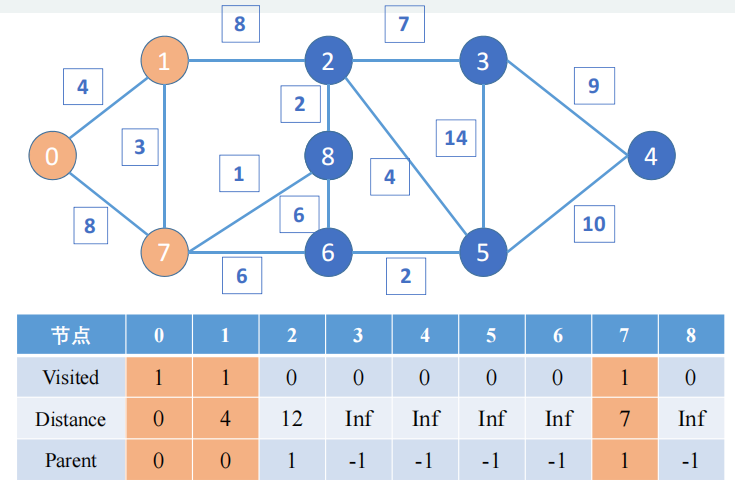
4️⃣ Repita los pasos anteriores y finalmente obtenga:

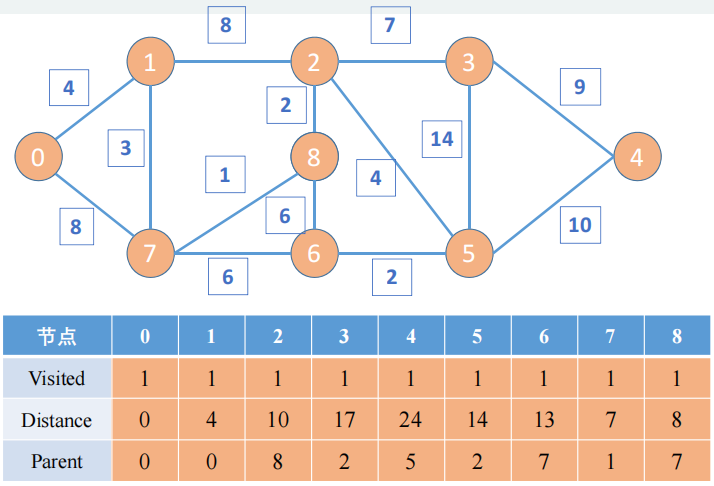
Según los resultados anteriores, podemos obtener la ruta más corta desde el nodo 0 al nodo 4:

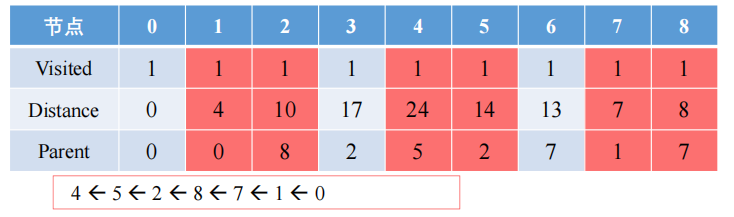
DijkstraEl algoritmo se usa generalmente para encontrar la ruta más corta en gráficos no dirigidos y también se puede usar en gráficos dirigidos, pero Dijkstrauna desventaja del algoritmo es que no se puede usar para procesar gráficos con pesos negativos.

Bellman‐Fordalgoritmo

Para solucionar Dijkstrala deficiencia de que el algoritmo no se puede utilizar para tratar gráficos con pesos negativos, se propone Bellman‐Fordun algoritmo.

De hecho, Bellman‐Fordel algoritmo ya no distingue los nodos entre visitados y no , porque Bellman‐Fordel algoritmo utiliza bucles para actualizar los pesos, y en cada bucle, Bellman‐Fordel algoritmo actualiza la información de todos los nodos.

Bellman‐FordEl algoritmo no admite gráficos que contengan ciclos de peso negativos (tampoco el algoritmo de Floyd)

4.2 Implementación del código

[P,d] = shortestpath(G,start,end [,'Method',algorithm])

• Función: Devuelve la ruta más corta de un nodo a otro Gen el gráficostartend

• Parámetros de entrada:

  • G: Gráfico de entrada ( graphobjeto u digraphobjeto)
  • start: nodo inicial
  • end: nodo objetivo
  • [,‘Method’,algorithm]: es un parámetro opcional que indica el algoritmo para calcular el camino más corto. Generalmente no necesitamos configurarlo manualmente, el valor predeterminado esauto
    

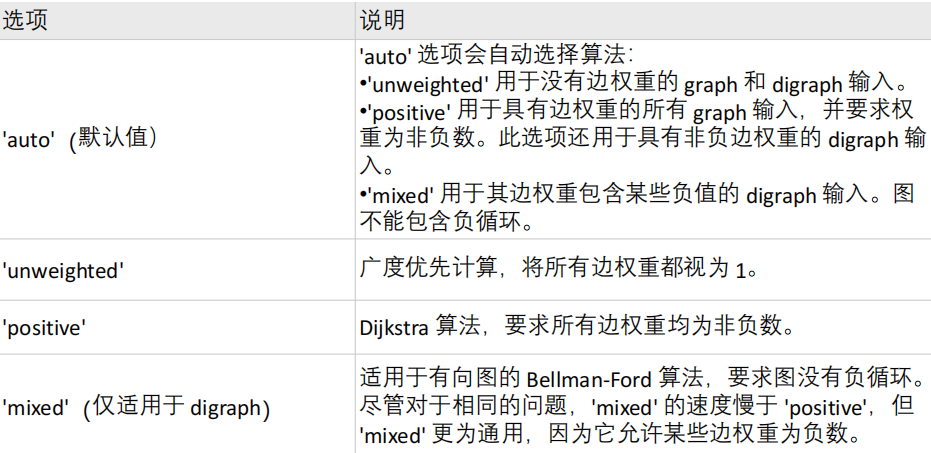
• Parámetros de salida:

  • PNodos pasados ​​por el camino más corto.
  • ddistancia más corta

Código de muestra:

%% 注意：以下代码需要较新版本的matlab才能运行（最好是2016版本及以上）
% 如果运行出错请下载新版的matlab代码再运行

% 注意哦，Matlab中的图节点要从1开始编号，所以这里把0全部改为了9
% 编号最好是从1开始连续编号，不要自己随便定义编号
s = [9 9 1 1 2 2 2 7 7 6 6  5  5 4];
t = [1 7 7 2 8 3 5 8 6 8 5  3  4 3];
w = [4 8 3 8 2 7 4 1 6 6 2 14 10 9];
G = graph(s,t,w);
plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2) 
set( gca, 'XTick', [], 'YTick', [] );  
[P,d] = shortestpath(G, 9, 4)  %注意：该函数matlab2015b之后才有哦

% 在图中高亮我们的最短路径
myplot = plot(G, 'EdgeLabel', G.Edges.Weight, 'linewidth', 2);  %首先将图赋给一个变量
highlight(myplot, P, 'EdgeColor', 'r')   %对这个变量即我们刚刚绘制的图形进行高亮处理（给边加上r红色）

% 求出任意两点的最短路径矩阵
D = distances(G)   %注意：该函数matlab2015b之后才有
D(1,2)  % 1 -> 2的最短路径
D(9,4)  % 9 -> 4的最短路径

% 找出给定范围内的所有点  nearest(G,s,d)
% 返回图形 G 中与节点 s 的距离在 d 之内的所有节点
[nodeIDs,dist] = nearest(G, 2, 10)   %注意：该函数matlab2016a之后才有

Gráficos de salida:

5 algoritmo de Floyd

5.1 Descripción general del algoritmo

FloydEl algoritmo es un algoritmo para resolver el camino más corto entre dos puntos cualesquiera y puede manejar correctamente el problema de camino más corto de gráficos no dirigidos o gráficos dirigidos (se permiten pesos negativos, pero no pueden existir bucles de pesos negativos).

FloydEn comparación con el algoritmo Dijkstrao Bellman‐Fordel algoritmo, el algoritmo puede encontrar el camino más corto entre dos puntos cualesquiera a la vez . Los dos últimos algoritmos solo pueden calcular el camino más corto entre el punto inicial dado y el punto final después de una ejecución. Por supuesto, Floydel tiempo de cálculo del algoritmo también es mayor que el de los dos últimos algoritmos. Los pasos centrales del algoritmo constan de tres capas de bucles.

Visualización de animación de algoritmo.

De las dos conclusiones observadas anteriormente, no nos resulta difícil extraer la siguiente idea:

• Supongamos que hay un punto inicial A y un punto final B, luego, para cualquier otro punto intermedio M:,
  D(A,B) ≤ D(A,M) + D(M,B)aquí, D (X, Y) representa la distancia más corta entre los dos puntos X e Y.

Por lo tanto, el núcleo del algoritmo de Floyd en realidad reside en un bucle de tres capas.

5.2 Implementación del código

☀️Realiza la distancia del camino más corto entre dos puntos cualesquiera

☀️Encontrar el camino más corto (registrar los puntos pasados ​​por el camino más corto)

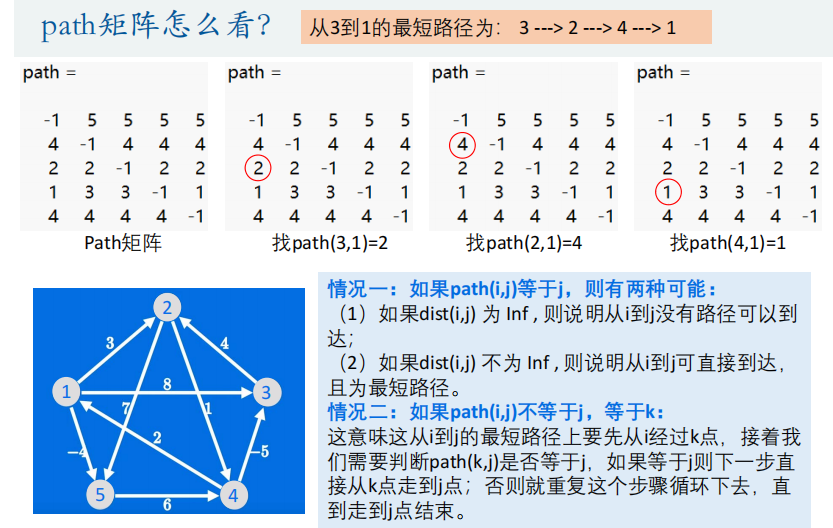
Convertir pseudocódigo a código Matlab :

1️⃣ Definir Floydfunciones de algoritmoFloyd_algorithm.m

function [dist,path] = Floyd_algorithm(D)
%% 该函数用于求解一个权重邻接矩阵任意两个节点之间的最短路径
% 输入：
%        D是权重邻接矩阵
% 输出：
%        dist是最短距离矩阵，其元素dist_ij表示表示i,j两个节点的最短距离
%        path是路径矩阵，其元素path_ij表示起点为i，终点为j的两个节点之间的最短路径要经过的节点

n = size(D,1);  % 计算节点的个数

% 初始化dist矩阵
dist = D;

% 下面我们来初始化path矩阵
path = zeros(n);
for j = 1:n
    path(:,j) = j;   % 将第j列的元素变为j
end
for i = 1:n
    path(i,i) = -1;  % 将主对角线元素变为-1
end

% 下面开始三个循环
for k=1:n    % 中间节点k从1- n 循环
   for i=1:n     % 起始节点i从1- n 循环
      for j=1:n    % 终点节点j从1-n 循环
          if dist(i,j)>dist(i,k)+dist(k,j)  % 如果i,j两个节点间的最短距离大于i和k的最短距离+k和j的最短距离
             dist(i,j)=dist(i,k)+dist(k,j);  % 那么我们就令这两个较短的距离之和取代i,j两点之间的最短距离
             path(i,j)=path(i,k);   % 起点为i，终点为j的两个节点之间的最短路径要经过的节点更新为path(i,k)
             % 注意，上面一行语句不能写成path(i,j) = k
          end
      end
   end
end

end

2️⃣ Defina una función que imprima la ruta más corta entre dos nodos cualesquieraprint_path.m

function [] = print_path(path,dist,i,j)
%% 该函数的作用是打印从i到j经过的最短路径
% 输入：
%        path是使用floyd算法求出来的路径矩阵
%        dist是使用floyd算法求出来的最短距离矩阵
%        i是起始节点的编号
%        j是终点节点的编号
% 输出：无

if i == j
    warning('起点和终点相同，请检查后重新输入')  % 在屏幕中提示警告信息
    return;  % 不运行下面的语句，直接退出函数
end
if path(i,j) == j   % 如果path(i,j) = j，则有两种可能：
% （1）如果dist(i,j) 为 Inf , 则说明从i到j没有路径可以到达
    if dist(i,j) == Inf
        disp(['从',num2str(i),'到',num2str(j),'没有路径可以到达'])
% （2）如果dist(i,j) 不为 Inf , 则说明从i到j可直接到达，且为最短路径
    else
        disp(['从',num2str(i),'到',num2str(j),'的最短路径为'])
        disp([num2str(i),' ---> ',num2str(j)])
        disp(['最短距离为',num2str(dist(i,j))])
    end
else  % 如果path(i,j) ~= j，则说明中间经过了其他节点：
    k = path(i,j);
    result = [num2str(i),' ---> '];  % 初始化要打印的这个字符串
    while k ~= j  % 只要k不等于j, 就一直循环下去
        result = [result , num2str(k) , ' ---> ' ];  % i先走到k这个节点处
        k = path(k,j);
    end
    result = [result , num2str(k)];
    disp(['从',num2str(i),'到',num2str(j),'的最短路径为'])
    disp(result)
    disp(['最短距离为',num2str(dist(i,j))])
end

end

3️⃣ Defina una función que imprima todos los caminos más cortos entre dos nodos cualesquiera.print_all_path.m

function [] = print_all_path(D)
%% 该函数的作用是求解一个权重邻接矩阵任意两个节点之间的最短路径,并打印所有的结果出来
% 输入：
%        D是权重邻接矩阵
% 输出：无

[dist,path] = Floyd_algorithm(D);   % 调用之前的Floyd_algorithm函数
n = size(D,1);
if n == 1
    warning('请输入至少两阶以上的权重邻接矩阵')   % 在屏幕中提示警告信息
    return;   % 不运行下面的语句，直接退出函数
end

for i = 1:n
    for j = 1:n
        if i ~= j  % 不等号用~=表示
            print_path(path,dist,i,j);   % 调用之前的print_path函数
            disp('-------------------------------------------')
            disp('  ')
        end
    end
end

end

4️⃣ Convierta el gráfico en una matriz de adyacencia ponderada D y llame Floyda la función del algoritmo

%% 首先将图转换为权重邻接矩阵D
n = 5;  %一共五个节点
D = ones(n) ./ zeros(n);  % 全部元素初始化为Inf【有向图】
for i = 1:n
    D(i,i) = 0;  % 主对角线元素为0
end
D(1,2) = 3;
D(1,3) = 8;
D(1,5) = -4;
D(2,5) = 7;
D(2,4) = 1;
D(3,2) = 4;
D(4,3) = -5;
D(5,4) = 6;
D(4,1) = 2;

%% 调用Floyd_algorithm函数求解
[dist,path] = Floyd_algorithm(D)

print_path(path,dist,1,5)
print_path(path,dist,1,4)
print_path(path,dist,3,1)

clc
disp('下面我们打印任意两点之间的最短距离：')
print_all_path(D)

6 preguntas para pensar

Encuentra el camino más corto entre dos puntos cualesquiera.

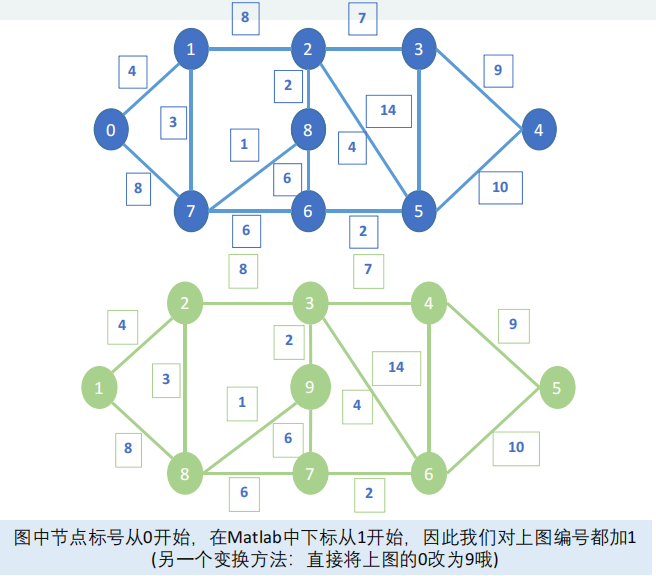
Respuesta de referencia:

%% 首先将图转换为权重邻接矩阵D
n = 9; %一共9个节点
D = zeros(n); % 全部元素初始化为0 【无向图】
% 因为是无向图，所以权重邻接矩阵是一个对称矩阵
D(1,2) = 4; D(1,8) = 8;
D(2,8) = 3; D(2,3) = 8;
D(8,9) = 1; D(8,7) = 6;
D(9,7) = 6; D(9,3) = 2;
D(7,6) = 2; D(3,4) = 7;
D(3,6) = 4; D(6,4) = 14;
D(4,5) = 9; D(6,5) = 10;
D = D+D'; % 这个操作可以得到对称矩阵的另一半
for i = 1:n
for j = 1:n
if (i ~= j) && (D(i,j) == 0) 
D(i,j) = Inf; % 将非主对角线上的0元素全部变为Inf
end
end
end
%% 调用Floyd_algorithm函数求解
[dist,path] = Floyd_algorithm(D)