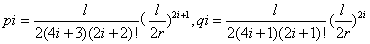缓和曲线参数再推导

〇、前言

在20世纪90年代之前，我国的高速公路还没有大规模建设，公路建设基本以二、三级甚至更低等级的公路为主，因此测量放样采用以前教科书上的切线支距法、偏角法等已经可以满足测量精度和工期的需要。随着20世纪80年代末90年代初高速公路建设事业的兴起，公路平面线型设计多样化，线型组合复杂，加之建设进度要求加快，相应精度要求也比普通公路要高，切线支距法、偏角法等已经不能满足测量精度和工期的需求了。因此必须采用坐标法精确计算平曲线上任意点的坐标，然后再采用坐标法进行放样。在计算坐标的过程当中，直线和圆曲线的计算方法简单，难点在于计算缓和曲线上任意点的坐标。在我国的公路、铁路工程平曲线设计中，普遍采用辐射螺旋线（又称回旋曲线）作为缓和曲线的线型计算模型（因此以下的缓和曲线均指回旋曲线）。为了计算缓和曲线上任意点的坐标，我们有必要从缓和曲线特性来推导出其代表参数的计算公式，进而为坐标的精确计算提供基础依据。

一、缓和曲线特性

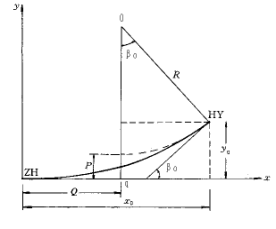
对于完整缓和曲线，设起点为ZH点，其半径r=∞，设终点为HY点，其半径r=R，起终点间缓和曲线全长为Ls；设p为缓和曲线上任意一点，曲率半径为r，该点至起点的曲线长度为l，根据回旋线特性：回旋线是半径与曲线长度成反比的曲线，则rl=RLs=C。其中C为常数，称为回旋线半径变化率，为今后计算方便，引入回旋曲线参数A，令A²=C。即当缓和曲线终点圆曲线半径（回旋线曲率半径）R及回旋线长度Ls已知时，C及A即可唯一确定。

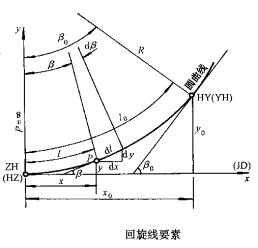
二、缓和曲线参数计算

1. 回旋曲线参数A的计算：根据前述缓和曲线特性，已经得出回旋曲线参数A的计算公式即：A²=C=rl=RLs。
2. 回旋线中心角（缓和曲线角）的计算：根据几何关系可知，回旋线上任意点p与缓和曲线起点之间的曲线长度l所对应的曲线中心角β即切线角，与p点切线与起点切线之间的夹角相等。在该p点取一微分弧段dl，所对应的中心角为dβ，于是有：
   
   ~~ $d\beta =\frac{dl}{r}=\frac{ldl}{C}=\frac{ldl}{RLs}\Rightarrow \beta =\int \frac{ldl}{RLs}=\frac{l^2}{2RLs}$ ~~
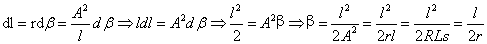
   则当l=Ls即缓和曲线终点处对应的缓和曲线圆心角为：
   β₀= $\frac{Ls^2}{2RLs}=\frac{Ls}{2R}=\frac{A^2}{2R^2}=\frac{Ls^2}{2A^2}$
3. 局部坐标参数计算 ：
   
   
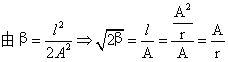
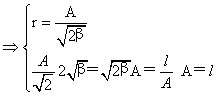
   建立以ZH点为原点，过该点的切线为x轴，法线为y轴的坐标系，则回旋线上任意点p的坐标为x，y，在该p点取一微分弧段dl，其在坐标轴上的投影分别为dx，dy，则有：
   $dx=dl·cosβ=rdβ·cosβ=\frac{A}{\sqrt{2β}}·cosβ\Rightarrow x=\frac{A}{\sqrt{2}}·∫\frac{cosβ}{\sqrt{β}}dβ$
   $dy=dl·sinβ=rdβ·sinβ=\frac{A}{\sqrt{2β}}·sinβ\Rightarrow y=\frac{A}{\sqrt{2}}·∫\frac{sinβ}{\sqrt{β}}dβ$
   而cos(β)和sin(β)的级数展开公式分别为：
   $cos(β)=1-\frac{β^2}{2!}+\frac{β^4}{4!}+……+(-1)^i·\frac{β^{2i}}{(2i)!}$(注：i＝0从第一项1开始)
   $sin(β)=\beta-\frac{β^3}{3!}+\frac{β^5}{5!}+……+(-1)^i·\frac{β^{2i+1}}{(2i+1)!}$(注：i＝0从第一项β开始)
   则有：
   
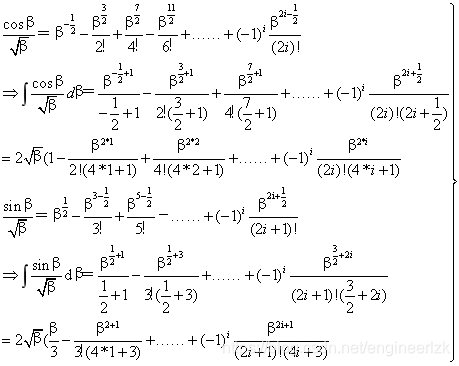
   将其入前述x，y的积分公式即可求出x，y的数值公式：
   
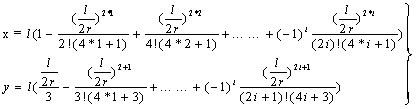
   将 $r=\frac{RLs}{l}$代入得:
   
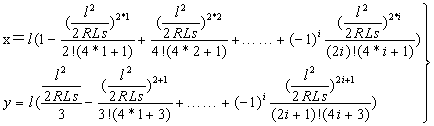
   由前式即可在已知R,Ls以及缓和曲线任意点p至起点缓和曲线长l的情况下计算p点的坐标，然后再通过坐标平移转换即可求出该点在全局坐标系下的坐标X,Y；由 $\beta=\frac{l^2}{2RLs}$即可求出p点的缓和曲线角，切线方位角也可由缓和曲线起点切线方位角+β的方式计算出来。至此，缓和曲线上任意点的坐标及方位角计算公式已推导完毕。
   从该式我们可以看出，如果在x值计算时取i=1，则 $x=l-\frac{l^5}{40R^2Ls^2}$,在y值计算时取i=0，则 $y=\frac{l^3}{6RLs}$，此两公式即为我们在教科书以及各种参考书上普遍见到的x，y值计算公式，也就是舍弃了高次项的近似公式表达式。
   为了描述方便，我们假定两个参数：
   
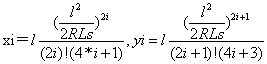
   测量施工人员可以根据设计精度要求(在实际施工测量中，若坐标精度达到1mm则完全满足规范和相关控制需求)，通过判断前述两个参数xi、yi的值是否小于精度要求值来确定x、y参数计算所需取的项数。
4. 曲线内移距p和切线增长值q的计算 ：
   
   由几何特性可知，p=y-r(1-cosβ)，q=x-rsinβ，将x、y、cosβ、sinβ的级数展开式代入并合并同类项后（推导过程略）得到：
   
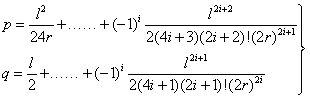
   为了防止在计算过程中
   
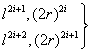
   数值溢出，也可将前述公式修改为：
   
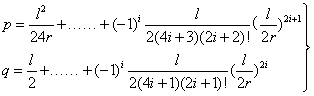
   当i取值0时， $p=\frac{Ls^2}{24R}，q=\frac{Ls}{2}$也是我们在教科书以及各种参考书上普遍见到的p，q值计算公式，也就是舍弃了高次项的近似公式表达式。
   同理，为了描述方便，我们假定pi，qi两个参数，测量施工人员可以根据设计精度要求(在实际施工测量中，若坐标精度达到1mm则完全满足规范和相关控制需求)，通过判断下述两个参数pi、qi的值是否小于精度要求值来确定p、q参数计算所需取的项数。