【机器学习】Logistic回归学习笔记(二) 梯度上升优化算法

机器学习实战（Machine Learning in Action）

CH05 logistic regression 学习笔记（一）梯度上升优化算法

import numpy as np
import math
%matplotlib inline
import matplotlib.pyplot as plt

def loadDataSet():
    dataMat = []
    labelMat = []
    with open('testdata.txt', 'r') as fr:
        for line in fr.readlines():
            lineArr = line.strip().split()
            dataMat.append([1, float(lineArr[0]), float(lineArr[1])])
            labelMat.append(int(lineArr[2]))
    return dataMat, labelMat

加载数据

返回 dataMat(list) 和 labelMat(list)

dataMat.len 为 (dataSize)(float)

labelMat.len 为 (dataSet)(int)

def sigmoid(inX):
    return 1.0/(1 + np.exp(-inX))

sigmoid 函数

$\sigma(z) = {{1}\over{1 + e^{-z}}}$

值得注意的是 $\sigma'(z) = \sigma(z)(1 - \sigma(z))$

sigmoid 函数经常被用于二分类，当 $\sigma(z) < 0.5$ 时，被认为 $P = 0$。而 $\sigma(z) \ge 0.5$ 时，被认为 $P = 1$。

在 logistic regression 里，我们把每个特征乘于一个回归系数，然后相加，将得到的总和带进 $\sigma(z)$ 中，得到一个 $0 \sim 1$ 的值。

即 $z = \omega_{0}x_{0} + \omega_{1}x_{1} + \cdots + \omega_{n}x_{n}$，如果采用向量的写法可以写成 $z = w^{T}x$。

其中， $\omega$ 是回归系数（权重）的了列向量，而 $x$ 是输入的特征值列向量。

因此我们现在剩下的问题就是如何求解回归系数（权重 $\omega$）。

def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    m, n = np.shape(dataMatrix)
    alpha = 0.001
    maxCycles = 100
    weights = np.ones((n, 1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)
        error = labelMat - h
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights

梯度上升(gradient ascent)

梯度

梯度是一个向量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该方向变化最快(梯度的方向)，变化率最大(梯度的模)。

我们将梯度记为 $\nabla$，则 $f(x,y)$ 的梯度为 $\nabla f(x,y) = \begin{bmatrix}\partial f(x,y)\over \partial x \\ \partial f(x,y) \over \partial y \end{bmatrix}$ 。

表示我们现在需要沿着 $x$ 轴移动 $\partial f(x,y)\over \partial x$，沿着 $y$ 轴移动 $\partial f(x,y)\over \partial y$ 。( $f(x,y)$ 要在这些点上有意义且可微)

但是我们上面的式子中，只给出了梯度的方向和变化率，并没有给出步长，因此我们还要定义一个步长 $\alpha$， $\alpha$ 也会被称之为学习率(learning rate)。

最优化权重

在本节中，我们讨论的分类为二分类，因此类别非0即1。
我们设 $x$ 为输入的特征向量， $\xi$ 为类别。

我们定义 $P(\xi = 1|x) = \sigma(z)$

显然 $P(\xi = 0|x) = 1 - P(\xi = 1|x) = 1 - {\sigma(z)} = \sigma(-z)$

因此，对于第 $i$ 个样本，有
$P(\xi = \xi_{i}|x_i) = P(\xi = 0|x_i)^{1-\xi_i}P(\xi = 1|x_i)^{\xi_i}=(1-\sigma(z_i))^{1-\xi_i}\sigma(z_i)^{\xi_i}$

由于各个样本之间是相互独立的，联合概率为各个样本的乘积。因此我们可以得到关于权重向量 $\omega$ 的最大似然函数
$\mathscr{L}(\omega) = \prod^n_{i = 1}(1-\sigma(z))^{1-\xi_i}(\sigma(z))^{\xi_i} \quad\text{($n$ 为样本总数)}$

两边同时取对数，得
$\begin{aligned} ln\ \mathscr{L}(\omega) & = \sum_{i=1}^{n}ln((1-\sigma(z))^{1-\xi_i}\sigma(z)^{\xi_i})\\ & = \sum_{i=1}^{n}((1-\xi_i)ln(1-\sigma(z)) + \xi_iln\ \sigma(z))\\ & = \sum_{i=1}^{n}((1-\xi_i)ln\ \sigma(-z_i) + \xi_iln\ \sigma(z_i))\\ \end{aligned}$
当 $\mathscr{L}(\omega)$ 最大时，此时的 $\omega$ 为回归系数最优解。

显然，若存在一个 $\omega$ 使得 $\mathscr{L}(\omega)$ 取得最大值，同样也可使 $ln\ \mathscr{L}(\omega)$ 取最大值。
因此，求解 $ln\ \mathscr{L}(\omega)$ 的最大值与求解 $\mathscr{L}(\omega)$ 的最大值是等效的。

现在的问题转换为求 $ln\ \mathscr{L}(\omega)$ 的最大值。

我们使用梯度上升求 $\omega$ 的最大值，即 $\omega := \omega +\alpha \nabla ln\ \mathscr{L}(\omega)$

对于 $\omega$ 的第 $j$ 个分量 $\omega_j$， 有 $\omega_j := \omega_j + \alpha {\partial ln\ \mathscr{L}(\omega) \over {\partial \omega_j}}$
$\begin{aligned}\\ {\partial ln\ \mathscr{L}(\omega) \over {\partial \omega_j}} & = \sum_{i=1}^n (-(1-\xi_i)(1 - \sigma(-z_i)) +\xi_i(1-\sigma(z_i))){\partial z_i \over \partial \omega_j}\\ & = \sum_{i=1}^n ((\xi_i - 1)\sigma(z_i) +\xi_i(1-\sigma(z_i)))x_j\\ & = \sum_{i=1}^n (\xi_i - \sigma(z_i))x_j\\ \end{aligned}$

即 ${\partial ln\ \mathscr{L}(\omega) \over {\partial \omega_j}} = x^T(\xi-\sigma(z))$
上述代码中，我们令 $error = \xi - \sigma(z)$

最后我们可以得到梯度上升的式子为 $\omega := \omega + \alpha x^T(\xi-\sigma(z))$

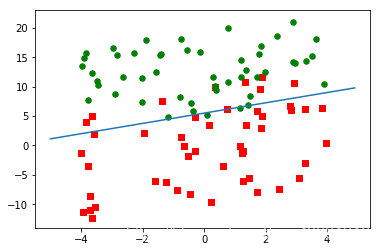
def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()
    dataArr = np.array(dataMat)
    n = np.shape(dataArr)[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i] == 1):
            xcord1.append(dataArr[i, 1])
            ycord1.append(dataArr[i, 2])
        else:
            xcord2.append(dataArr[i, 1])
            ycord2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s = 30, c = 'red', marker = 's')
    ax.scatter(xcord2, ycord2, s = 30, c = 'green')
    x = np.arange(-5.0, 5.0, 0.1)
    y = (-weights[0] - weights[1] * x)/weights[2]
    ax.plot(x, y)
    plt.show()

dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
print(weights)
plotBestFit(weights.getA())

[[ 1.65879592]
[ 0.2642799]
[-0.30190436]]