简单线性回归

简单线性回归围绕一个响应变量和解释变量的某个特征之间的关系进行建模。
讨论问题：
“如何对模型进行拟合”
虽然简单的线性回归对于现实世界的问题几乎不具有可用性，但是理解简单线性回归是理解许多其他模型的关键。
本文将学习简单线性回归的一般模型，并将他们运用到现实世界的数据集。

1. 简单线性回归-为何简单

大家回想一下，回归问题的目的是去预测一个连续响应变量的值。
我们举个例子：

通过披萨的尺寸来预测价格

ID	直径（英寸）	价格(RMB)
1	6	7
2	8	9
3	10	13
4	14	17.5
5	18	18

表1.1 披萨价格尺寸表

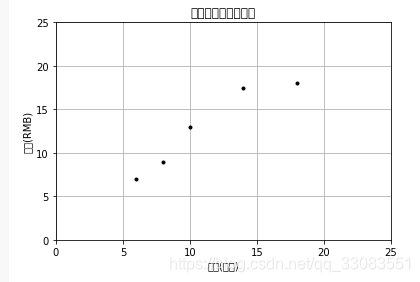
1. 我们用matplotlib作图来将训练数据可视化

导入包
创建解释变量和响应变量
画图
最后结果如下：

完整代码如下：

import numpy as np
import matplotlib.pyplot as plt
#Numpy库和Matplotlib库不用我说了吧~~
#在scikit-learn中的一个惯用法是将特征向量的矩形命名为X<-大写
#大写字母表示矩阵，小写字母表示向量
X = np.array([[6], [8], [10], [14], [18]]).reshape(-1,1)
#X表示披萨的直径
y = [7, 9, 13, 17.5, 18]
#y表示价格向量
plt.figure()
plt.title('披萨价格尺寸散点图')
plt.xlabel('直径(英寸)')
plt.ylabel('价格(RMB)')
plt.plot(X, y, 'k.')
plt.axis([0, 25, 0, 25])
plt.grid(True)
plt.show()

从训练数据中心我们可以看出披萨的直径和价格之间存在正相关关系，这个结论我们日常也可以得出。
接下来我们需要

2. 对这个关系进行建模

直接用sklearn的linear_model就可以

from sklearn.linear_model import LinearRegression
model = LinearRegression() #创建一个估计器实例
model.fit(X, y)#用训练数据拟合模型
test_pizza = np.array([[12]])
predicted_price = model.predict(test_pizza)[0]
#预测一个新的直径披萨的价格
print('直径12的披萨价格为：%.2f 元' %predicted_price)

简单线性模型假设响应变量和解释变量之前存在线性关系，它使用一个被称为超平面的线性平面来对这种关系进行建模。
一个超平面是一个子空间，它比组成它的环绕空间小一个维度。在简单线性回归中共有两个维度，一个维度表示响应变量，另一个维度表示解释变量。因此，回归超平面只有一个维度，一个一维的超平面是一条直线。
LinearRegression类是一个估计器，估计器基于观测到的数据预测一个值。在scikit-learn中，所有的估计器都实现了fit方法和predict方法。前者用于学习模型的参数，后者使用学习到的参数来预测一个解释变量对应的响应变量值。
LinearRegression的fit方法学习了公式简单线性回归模型的参数：

y = α+βx               公式1.1

在上面的公式中，y是响应变量的预测值，在这个例子中，它表示披萨的预测价格，x表示将解释变量，α和β都是通过学习算法学到的模型参数。
利用训练数据学习产生最佳拟合模型的简单线性回归的参数值称为普通最小二乘（Ordinary Lease Squares, OLS）或者线性最小二乘。

2. 用代价函数评价模型的拟合性

实际当中，一个参数的集合绘制，往往会产生几条回归线。那么问题来了，如何评估哪组参数值产生了最佳拟合回归线呢？
代价函数
代价函数，也称为损失函数，它用于定义和衡量一个模型的误差。
本例子中，由模型预测出的价格和在训练数据集中观测到的披萨价格之间的差值被称为残差或者训练误差。
我们可以通过最小化残差的和来生成最佳披萨价格预测器。也就是说，对于所有训练数据而言，如果模型预测的响应变量都接近观测值，那么模型就是拟合的。
这种衡量模型拟合的方法叫做残差平方和（RSS）代价函数。
在形式上，该函数通过对所有训练数据的残差平方求和来衡量模型的拟合性。
RSS由下面的方程公式计算出：
$SS_{res}=\sum_{n}^{i=1}(y_{i}-f(x_{i}))^{2}$ ----------------- 公式1.2
有了公式就好办了，来人，上代码：

print("残差平方和代价函数为: %.2f " %np.mean((model.predict(X)-y)**2))

结果如下：
在这里插入图片描述
到这一步，我们有了一个代价函数，可以通过求这个函数的极小值来找出模型的参数值。

3. 求解简单的线性回归的OLS

回想一下，简单线性回归由方程公式1.1给出，而我们的目标是通过求代价函数的极小值来求解出α和β的值。
首先，先求解β
这里需要引入协方差这个概念。我们需要计算x的方差以及x和y的协方差。

3.1 方差

方差用来衡量一组值偏离程度，如果集合中的所有数值都相等，那么这组数值的方差为0.方差小意味着这组值都很接近总体均值，而如果集合中包括偏离均值很远的数据则集合会有很大的方差。
方差可以使用下面的公式1.3算出：
$var(x)=\frac{\sum_{n}^{i=1}(x_{i}-\bar{x})^{2}}{n-1}$ -------------公式1.3
$ \bar{x} $表示x的均值，$ x_{i}$是训练数据中第i个x的值，n表示训练数据的总量。
接下来计算一下训练数据中披萨直径的方差，代码如下：

X=np.array([[6], [8], [10], [14], [18]]).reshape(-1, 1)
x_bar = X.mean()
print('平均值为：',x_bar)
#这里在计算样本方差的时候将样本的数量减去1
#这个技巧称为贝塞尔矫正，它的作用是纠正了对样本中总体方差估计的偏差
variance = ((X -x_bar)**2).sum() /(X.shape[0]-1)
print('方差是：',variance)

Numpy库也提供了一个叫做var的方法来计算方差。
计算样本方差时关键字参数ddof可以设置贝塞尔矫正，代码如下：

print(np.var(X,ddof=1))

结果如下：
在这里插入图片描述

3.2 协方差

协方差用来衡量两个变量如何一同变化。
如果变量一起增加，它们的协方差为证。如果一个变量增加时另外一个变量减少，他们的协方差为负。如果这两个变量之间没有线性关系，它们的协方差为0，它们是线性无关但是不一定是相对独立的。
协方差可以使用下面的公式计算：
$cov(x,y)=\frac{\sum_{n}^{i=1}(x_{i}-\bar{x})(y_{i}-\bar{y}))}{n-1}$
和方差一样， $x_{i}$ 是训练数据中第i个x的值， $\bar{x}$ 表示披萨直径的均值， $\bar{y}$ 表示价格的均值， $y_{i}$ 表示训练数据中第i个y的值，n表示训练数据的总量。
我们来计算一下训练数据中披萨半径和价格的协方差：
代码如下：

y = np.array([7, 9, 13, 17.5, 18])
y_bar = y.mean()
#因为所有的操作是行向量，所以把x转置
covariance = np.multiply((X - x_bar).transpose(), y - y_bar).sum() /(X.shape[0] - 1)
print('协方差为:',covariance)
#看看Numpy自带的
print(np.cov(X.transpose(),y)[0][1])

结果图如下：
在这里插入图片描述
到这里，我们已经计算出了解释变量的方差以及解释变量和响应变量之间的协方差，接下来需要求解出β
公式和结果如下：
$b=\frac{cov(x,y)}{var(x)}$ ( β显示错误，用b来表示，但是请读者注意，这里是 β)
把数字代入得：
$b=\frac{22.65}{23.2} =0.98$
现在我们获得了β的值，，接下来我们需要求解α，
$a = \bar{y}-b\bar{x}$
这里 $\bar{y}$ 是y的均值， $\bar{x}$ 是x的均值。 $(\bar{x},\bar{y})$ 是质心坐标，是一个模型必须经过的点。
$a = 12.9 - 0.98x11.2 = 1.92$
ok，到此，已经通过代价函数的极小值解除了模型的参数值，可以代入披萨的直径预测他们的价格。
（一元二次方程，，，这就是传说中：简单线性回归！！！）

4. 评价模型

到这里，我们已经使用了一种学习算法从训练数据中估计出了模型的参数。我们如何评估模型是否很好的表达了现实中解释变量和响应变量之间的关系呢？
表2：评价模型测试实例

测试实例	披萨直径	实际价格	预测价格
1	8	11	9.77
2	9	8.5	10.75
3	11	15	12.70
4	16	18	17.59
5	12	11	13.68

本文使用一种叫做R方的方法。
R方，也叫决定系数，它用来衡量数据和回归线的贴近程度。计算R方的方法有很多种，在简单线性回归模型中，R方等于皮尔森积差相关系数（PPMCC）的平方，也被称为皮尔森相关系数r的平方。使用该计算方法，R方必须是0和1之间的正数。
原因非常简单和直观：如果R方描述的是由模型解释的响应变量中的方差的比例，这个比例不能大于1或者小于0.
了解性能指标的局限性非常重要，R方对于异常值尤其敏感，新的特征增加到模型中时，它常常会出现异样增长。
我们通过scikit-learn使用的方法来计算披萨价格预测器R方。首先我们需要算出平方总和。
$y_{i}$ 是第i个测试实例的响应变量观测值， $\bar{y}$ 是响应变量的观测值均值。
$SS_{tot}=\sum_{n}^{i=1}(y_{i}- \bar{y})^{2}$
以我们表格里面数据为例：
$SS_{tot}=(11-12.7)^{2}+(8.5-12.7)^{2}+....+(11-12.7)^{2}=56.8$
此外，我们还要计算出RSS
回顾之前的RSS公式1.2：
$SS_{res}=\sum_{n}^{i=1}(y_{i}-f(x_{i}))^{2}$
把数字带进去就应该是：
$SS_{res}=(11-9.78)^{2} +(8.5-10.75)^{2} +.....+(11-13.68)^{2}=19.20$
最后,我们来求R方
$R^{2}= 1-\frac{SS_{res}}{SS_{tot}}$
代入具体数字就是：
$R^{2}= 1-\frac{19.20}{56.8} =0.66$
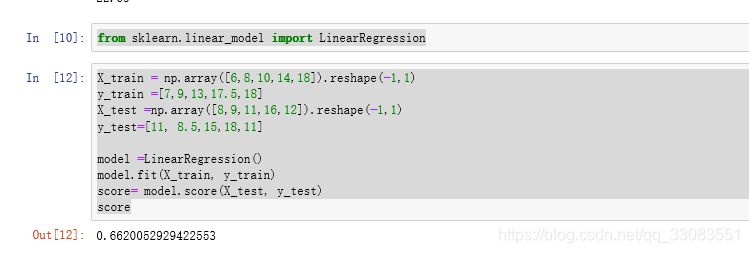
R方计算得分为0.662，这表明测试实例价格变量的方差很大比例上是可以被模型解释的。
接下来，用scikit-learn来印证：
代码如下：
在这里插入图片描述