根据三角恒等式
$$cos(n+1)\theta +cos(n-1)\theta =2cos\theta \cdot cos(n\theta)$$
令$\theta=arccost$,则对于函数
$${P}_{n}(t)=cos((n-1)arccost),-1\leqslant t\leqslant 1\text{ }\left( n=1,2,\cdots \right)$$
有递推关系
$${P}_{n+1}(t)=2t \cdot {P}_{n}(t) - {P}_{n-1}(t)$$
由上式推出的多项式为第一类切比雪夫多项式,其前几个形式为
$$\left\{\begin{matrix}
\\ {P}_{1}(t)=1
\\ {P}_{2}(t)=t
\\ {P}_{3}(t)=2{{t}^{2}}-1
\\ {P}_{4}(t)=4{{t}^{2}}-3t
\\ {P}_{5}(t)=8{{t}^{4}}-8{{t}^{2}}+1
\\ {P}_{6}(t)=16{{t}^{5}}-20{{t}^{3}}+5t
\\ {P}_{7}(t)=32{{t}^{6}}-48{{t}^{4}}+18{{t}^{2}}-1
\\\vdots
\end{matrix}\right.$$
—个n次多项式可以表示为多个切比雪夫多项式的加权和,在NumPy中,使用Chebyshev类表示由切比雪夫多项式组成的多项式:
$$f\left( t \right)=\sum\limits_{i=0}^{n}{{{a}_{i}}}{{P}_{i}}\left( t \right)$$
${{P}_{i}}\left( t \right)$多项式可以通过Chebyshev.basis(i)获得,通过多项式类的conveit()方法可以在不同类型的多项式之间相互转换,转换的目标类型由kind参数指定,多项式各项的系数按照从小到大的顺序排列。
from numpy.polynomial import Polynomial, Chebyshev
P1 = Chebyshev.basis(1).convert(kind=Polynomial)
P6 = Chebyshev.basis(6).convert(kind=Polynomial)
P1: poly([0. 1.])
P6: poly([ -1. 0. 18. 0. -48. 0. 32.])
上所示即为多项式的系数,如果想得到表达式,如下
from numpy.polynomial import Polynomial, Chebyshev
from sympy import *
P6 = Chebyshev.basis(6).convert(kind=Polynomial)
t = Symbol('t')
P6(t)
1.0*t**2*(1.0*t**2*(32.0*t**2 - 48.0) + 18.0) - 1.0
如上所示即为第六个切比雪夫不等式。
${a}_{i}$的获得则需要知道$f\left( t \right)$的坐标点,假设已知其五个坐标点(2,6)、(3,9)、(4,10)、(5,15)、(6,19),由于有五个点,故x最高次数为4次方,所以
$$f\left( t \right)=\sum\limits_{i=0}^{4}{{{a}_{i}}}{{P}_{i}}\left( t \right)$$
将其五个点坐标代入,
$$f\left( 2 \right)={{a}_{0}}{{P}_{0}}\left( 2 \right)+{{a}_{1}}{{P}_{1}}\left( 2 \right)+{{a}_{2}}{{P}_{2}}\left( 2 \right)+{{a}_{3}}{{P}_{3}}\left( 2 \right)+{{a}_{4}}{{P}_{4}}\left( 2 \right)=6$$
$$f\left( 3 \right)={{a}_{0}}{{P}_{0}}\left( 3 \right)+{{a}_{1}}{{P}_{1}}\left( 3 \right)+{{a}_{2}}{{P}_{2}}\left( 3 \right)+{{a}_{3}}{{P}_{3}}\left( 3 \right)+{{a}_{4}}{{P}_{4}}\left( 3 \right)=9$$
$$f\left( 4 \right)={{a}_{0}}{{P}_{0}}\left( 4 \right)+{{a}_{1}}{{P}_{1}}\left( 4 \right)+{{a}_{2}}{{P}_{2}}\left( 4 \right)+{{a}_{3}}{{P}_{3}}\left( 4 \right)+{{a}_{4}}{{P}_{4}}\left( 4 \right)=10$$
$$f\left( 5 \right)={{a}_{0}}{{P}_{0}}\left( 5 \right)+{{a}_{1}}{{P}_{1}}\left( 5 \right)+{{a}_{2}}{{P}_{2}}\left( 5 \right)+{{a}_{3}}{{P}_{3}}\left( 5 \right)+{{a}_{4}}{{P}_{4}}\left( 5 \right)=15$$
$$f\left( 6 \right)={{a}_{0}}{{P}_{0}}\left( 6 \right)+{{a}_{1}}{{P}_{1}}\left( 6 \right)+{{a}_{2}}{{P}_{2}}\left( 6 \right)+{{a}_{3}}{{P}_{3}}\left( 6 \right)+{{a}_{4}}{{P}_{4}}\left( 6 \right)=19$$
矩阵表示为:
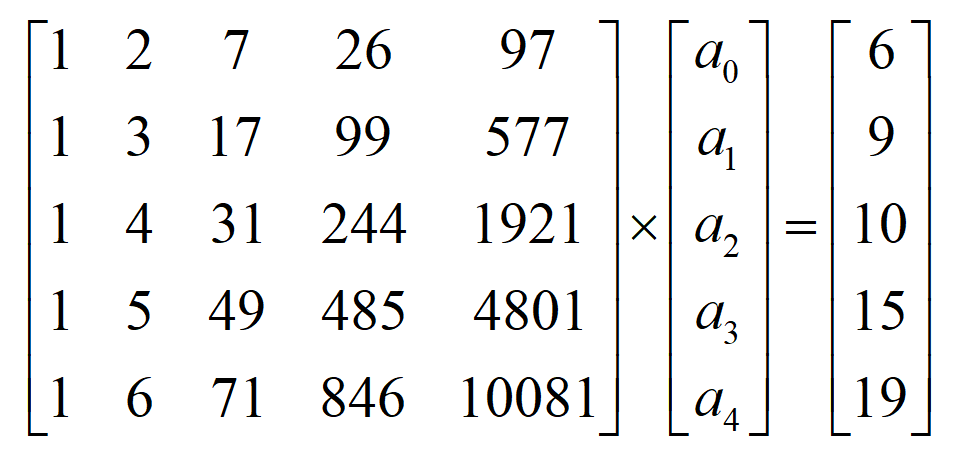
由上述方程组即可解得${a}_{i}$。Numpy库里numpy.polynomial.chebyshev模块提供了chebvander函数可以自动完成上述计算过程,称虚范德蒙矩阵。
import numpy as np
import numpy.polynomial.chebyshev as chebyshev
import numpy.linalg as linalg
x = np.array([2, 3, 4, 5, 6])
y = np.array([5, 9, 10, 15, 19])
deg = len(x) - 1
R = chebyshev.chebvander(x, deg)
A = linalg.solve(R, y)
R: [[1.0000e+00 2.0000e+00 7.0000e+00 2.6000e+01 9.7000e+01]
[1.0000e+00 3.0000e+00 1.7000e+01 9.9000e+01 5.7700e+02]
[1.0000e+00 4.0000e+00 3.1000e+01 2.4400e+02 1.9210e+03]
[1.0000e+00 5.0000e+00 4.9000e+01 4.8500e+02 4.8010e+03]
[1.0000e+00 6.0000e+00 7.1000e+01 8.4600e+02 1.0081e+04]]
A: [-1.23937500e+02 1.24958333e+02 -2.40000000e+01 2.04166667e+00 -6.25000000e-02]
A即为所需求系数${a}_{i}$。