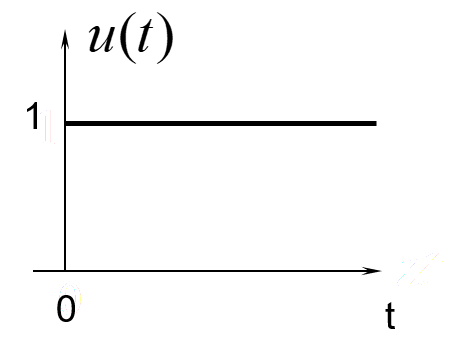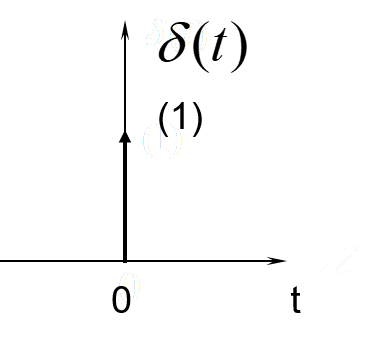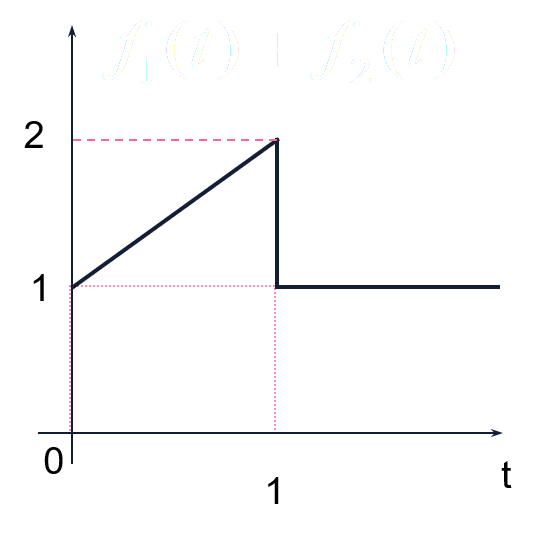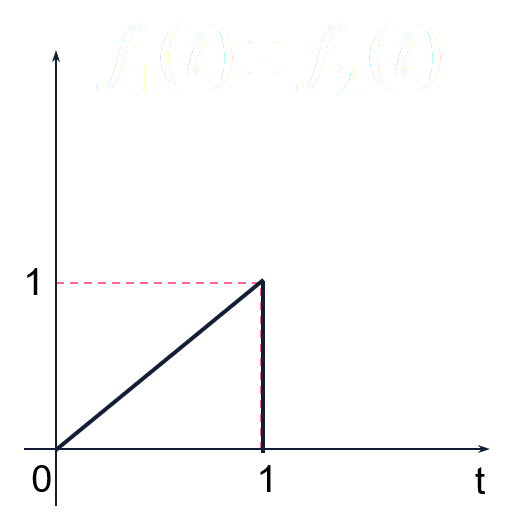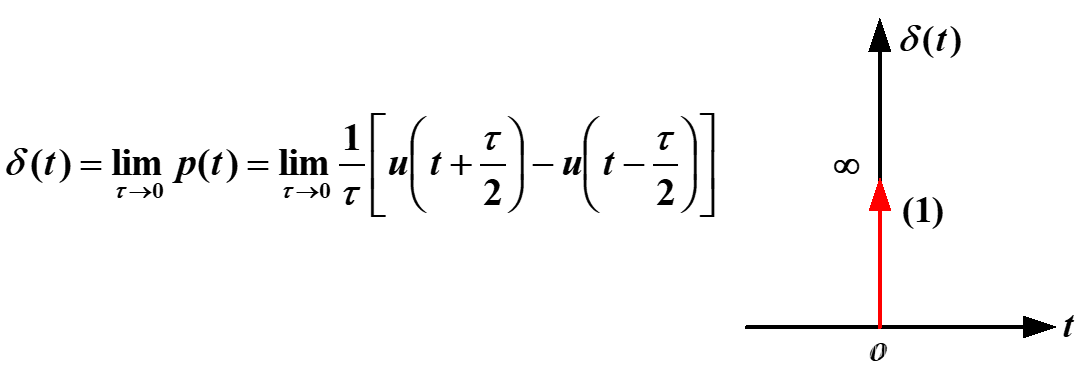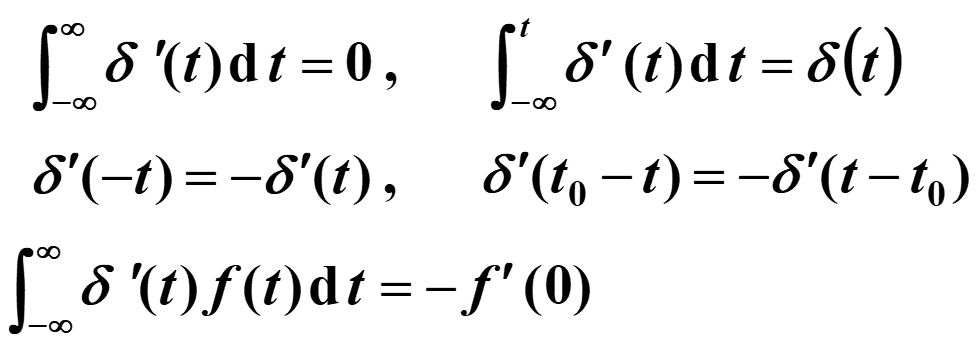原文请前往 https://blog.csdn.net/qq_42635142/article/details/88380966
信号的分类
确定信号和随机信号
{确定信号:可以用确定时间函数表示的信号随机信号随机信号:信号不能用确切的函数描述,在任意时刻的取值都具有不确定性,只可能知道它的统计特性
一些确定信号比如正弦波、余弦波、方波等
一些随机信号比如股市的k线,语音信号等
连续信号和离散信号
{连续信号:在连续的时间范围内有定义的信号称为连续时间信号离散信号:在一些离散的瞬间才有定义的信号称为离散时间信号

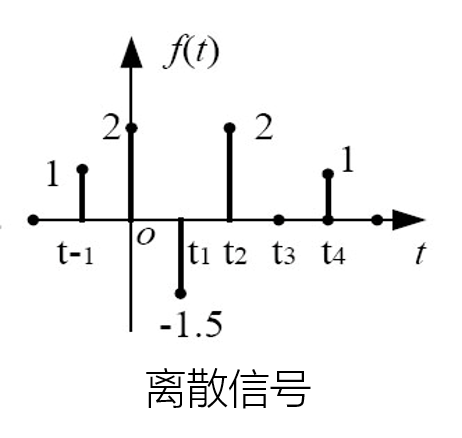
离散信号可表示为
x(nT),通常取等间隔T,简写为x(n),这种等间隔的离散信号也常称为序列。其中k称为序号。
周期信号和非周期信号
{周期信号:是指一个每隔一定时间T,按相同规律重复变化的信号非周期信号:不具有周期性的信号称为非周期信号
周期信号的规律
- 两个周期信号
x(t),y(t)的周期分别为
T1和T2,若其周期之比
T1/T2为有理数,则其和信号
x(t)+y(t)仍然是周期信号,其周期为
T1和T2的最小公倍数。
- 两连续周期信号之和不一定是周期信号,而两周期序列之和一定是周期序列
- 连续正弦信号一定是周期信号,而正弦序列不一定是周期序列
{sin2t+cos3t是周期信号sinπt+cos2t不是周期信号
信号类型的分辨
- 数字信号与离散信号:数字信号属于离散信号,但二者并不是完全等价,幅值为有限个的离散信号才是数字信号。比如某个离散信号,只取0,1,2这几个数的幅值,这便是数字信号,若是赋值范围是无限大,那就不是数字信号
典型连续时间信号
正弦信号
f(t)=Ksin(ω+θ)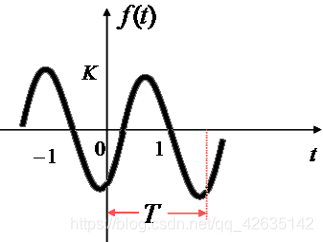
- 周期
T=ω2π
- 角频率
ω=2πf
- 正弦信号对时间的积分、微分后仍然是同频率余弦
指数信号
f(t)=Keat
τ=∣a∣1
- 指数信号对时间的微、积分仍是指数
-
⎩⎪⎨⎪⎧a>0:信号将随时间而增长a<0:信号将随时间而衰减a=0:直流信号
-
τ为指数信号时间常数,
τ越大,信号变化(增长或衰减)越快
复指数信号
f(t)=Kest,s=σ+jω
f(t)=Keat=Keσtcos(ωt)+Keσtsin(ωt)
-
s=σ+jω为复数,称为复频率
-
σ,ω都是实常数
-
σ的量纲是
1/s,
ω的量纲是
rad/s
-
⎩⎪⎨⎪⎧σ=0,ω=0:直流信号σ>0,ω=0:升指数信号σ<0,ω=0:衰减指数信号
- 振荡信号
⎩⎪⎨⎪⎧σ=0,ω̸=0:等幅σ>0,ω̸=0:增幅σ<0,ω̸=0:衰减
阶跃信号
单位阶跃信号:
u(t)={0 (t<0)1 (t>0)
图像表示:
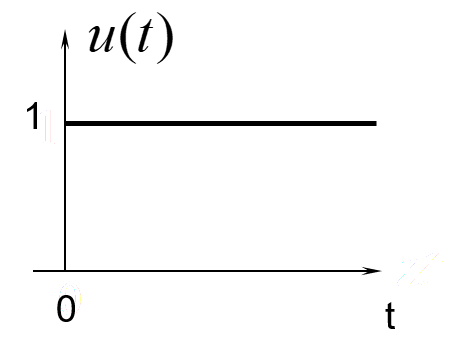
冲激信号
{δ(t)=0 (t̸=0)∫−∞∞δ(t)dt=1 (t>0)
图像表示:
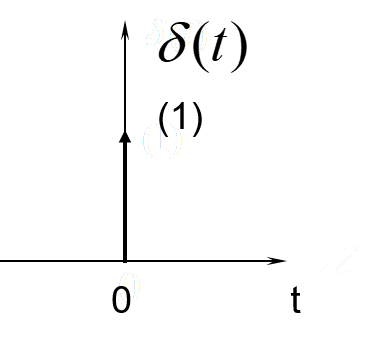
(在后面会对冲激信号和阶跃信号详细阐述)
抽样信号
Sa(t)=tsint
-
Sa(−t)=Sa(t),即它是偶函数
-
t→0limSa(t)=1
-
t→∞limSa(t)=0
-
Sa(t)=0⟹t=±nπ (n=1,2,3....)
-
∫0∞Sa(t)dt=2π,∫−∞∞Sa(t)=π
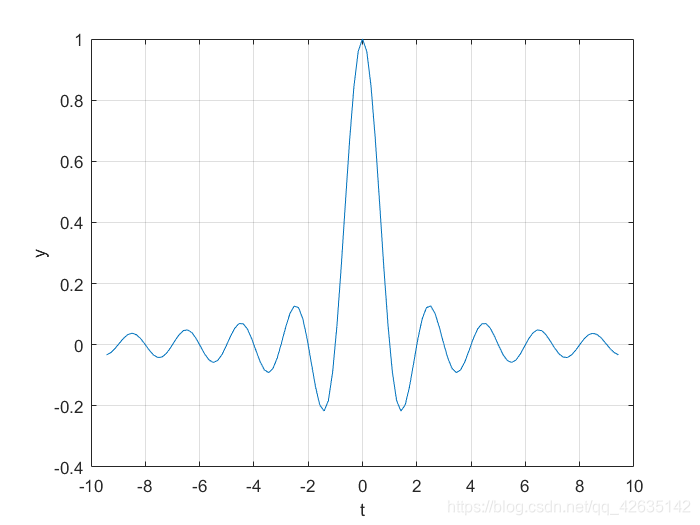
% matlab 代码
clear ;
close all;
clc;
t=-3*pi:pi/20:3*pi;
y=sinc(t);
plot(t,y);
xlabel('t');
ylabel('y');
grid on;
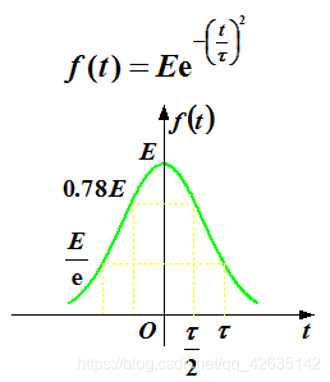
钟形脉冲函数(高斯函数)
f(t)=Ee−(τt)2
信号的基本运算
- 常规运算
{线性运算乘除运算
- 数学运算
{微分运算积分运算
- 波形变换
⎩⎪⎨⎪⎧反褶变换移位变换尺度变换
- 相互运算
{卷积运算相关运算
信号的四则运算
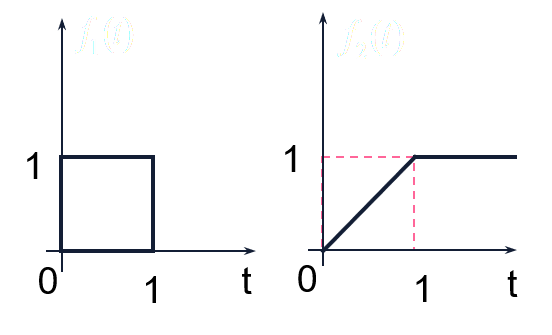
两信号的相加、相减、相乘运算指同一时刻两信号之值对应相加减乘
如下图两信号
f1(t)和f2(t):
f1(t)+f2(t):
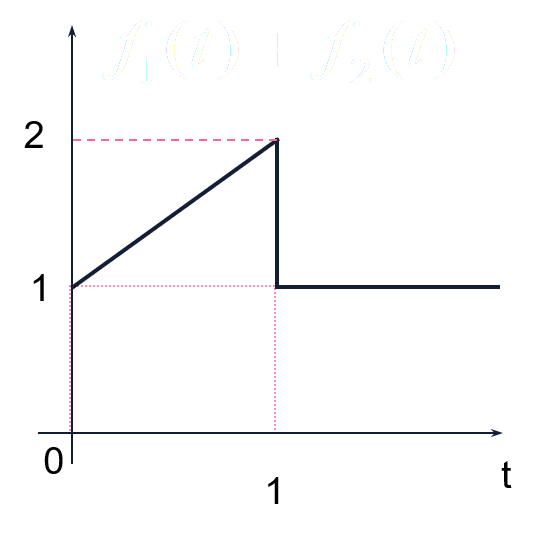
f1(t)×f2(t):
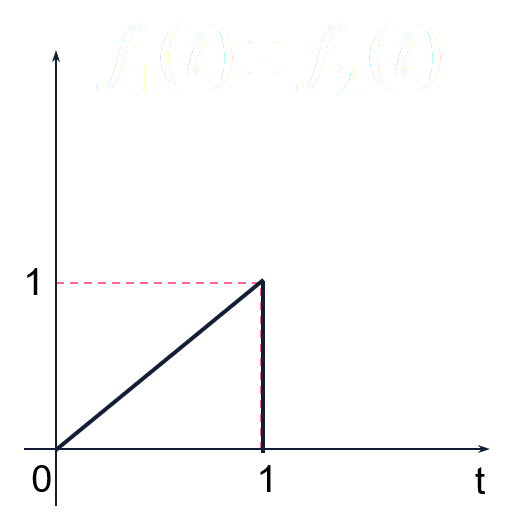
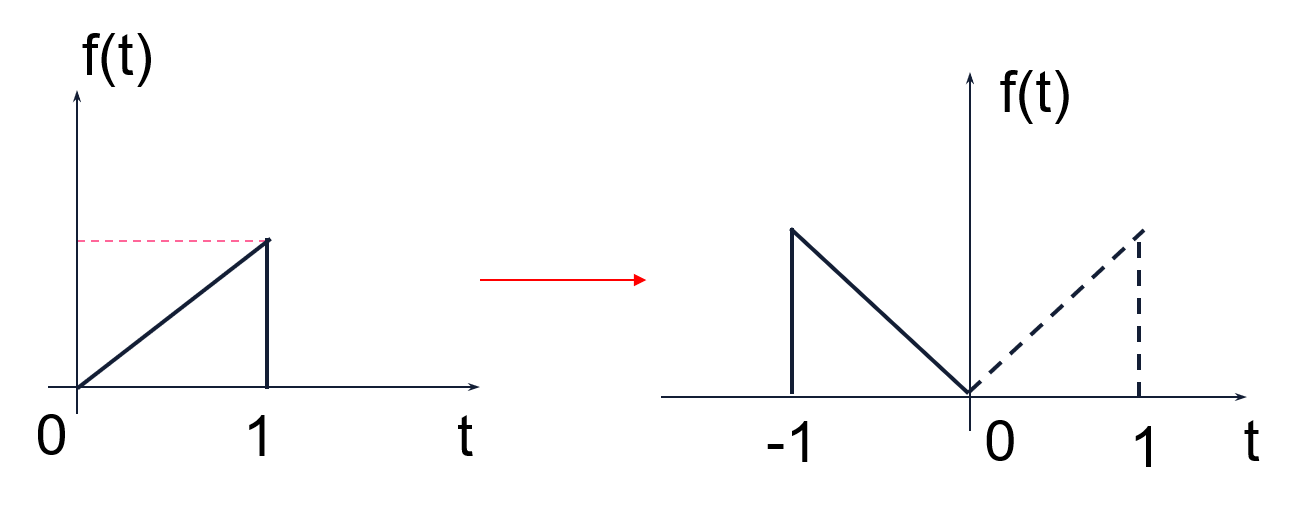
信号的波形变换
反褶
将
f(t)→f(−t),
x(n)→x(–n) 称为对信号
f的反转或反折。从图形上看是将
f 以纵坐标为轴反转180度
移位
遵循“左加右减”原则,即
f(t+t0)时,图像向左平移,
f(t−t0)时,图像向右平移(这里
t0>0)
尺度变换
遵循“大缩小展”原则,即
f(at)中,
{a>1 图像压缩为原来的a1a<1 图像展开为原来的a1倍
(这里
a>0)
几种变换组合
移位、反褶、尺度变换相结合,三种运算的次序可任意。但一定要注意始终对时间t 进行。
例如:
f(t)→f(−2t−4)
-
先移位、再尺度变换、最后反褶.
右移四位:
f(t)→f(t−4)
压缩1/2:
f(t−4)→f(2t−4)
反褶:
f(2t−4)→f(−2t−4)
(可以注意到,在尺度变换的时候,进行的是
2t−4而不是
2(t−4),反褶也是只对
t加了负号)
-
尺度变换、再移位、最后反褶
压缩1/2:
f(t)→f(2t)
右移两位:
f(2t)→f(2(t−2))→f(2t−4)
反褶:
f(2t−4)→f(−2t−4)
-
先反褶,再移位,最后尺度变换
反褶:
f(t)→f(−t)
左移四位:
f(−t)→f(−t−4)
压缩1/2:
f(−t−4)→f(−2t−4)
(先进行反褶会增大变换难度,所以反褶一般最后处理)
信号的积分和微分
- 微分:信号f(t)的微分运算指
f(t)对
t取导数,即
f′(t)=dtdf(t)
- 积分:信号f(t)的积分运算指
f(t)在
(−∞,t)区间内的定积分,表达式为:
∫−∞tf(τ)dτ
信号的微分和积分作用效果:
- 信号经过微分运算后突出显示了它的变化部分,起到了锐化的作用
- 信号经过积分运算后,使得信号突出变化部分变得平滑了,起到了模糊的作用;利用积分可以削弱信号中噪声的影响。
即:微分
→锐化;积分
→平滑
阶跃信号和冲激信号
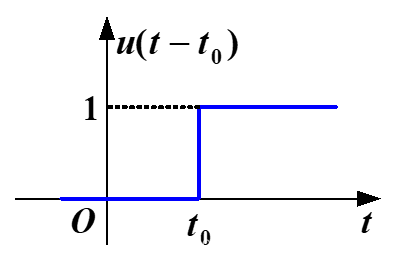
单位阶跃信号
u(t)={0 (t<0)1 (t>0)
有延迟的单位阶跃信号
u(t−t0)={0 (t<t0)1 (t>t0)
即当
t0>0时,信号向右做
t0个单位的平移变换:
阶跃信号的应用——窗函数(门函数)
Gτ(t)=u(t+2τ)−u(t−2τ)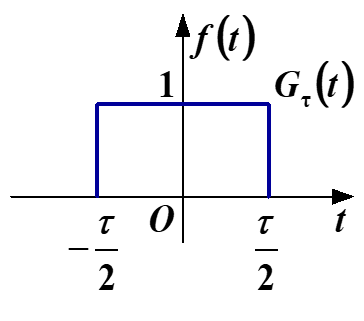
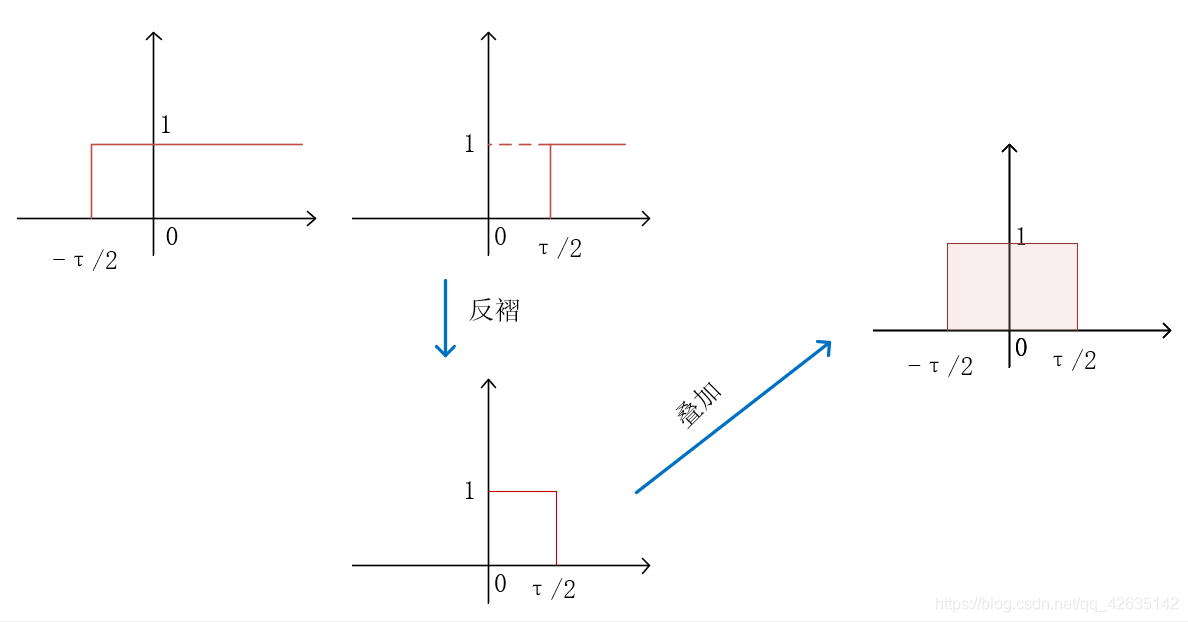
窗函数的应用:
- 任何信号乘以一个窗函数,就只剩窗函数“窗口”里的内容了
如: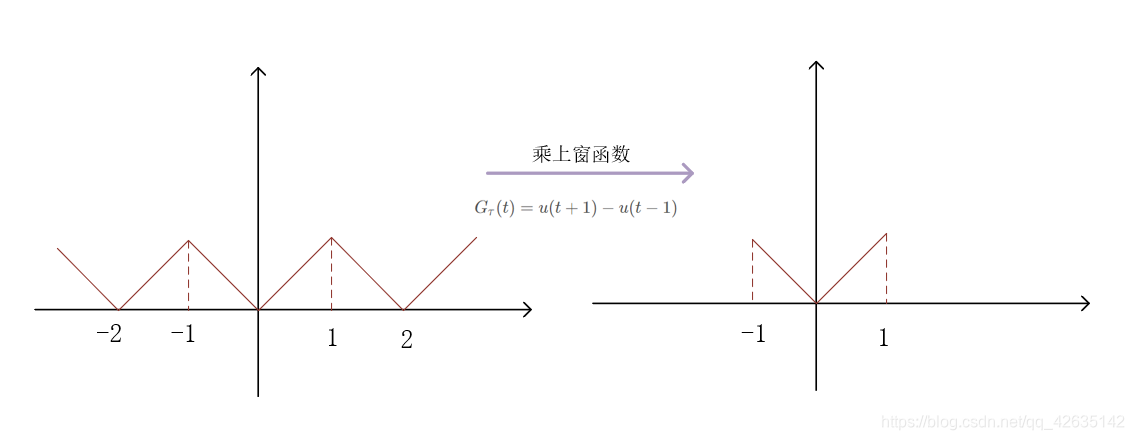
- 特殊函数的表示,如
sgn(x)
sgn(x)={1 (t>0)−1 (t<0)=u(t)−u(−t)=2u(t)−1
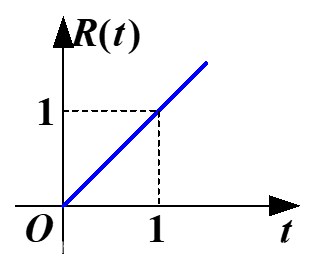
单位阶跃信号的积分——单位斜变信号
R(t)={0 (t<0)t (t⩾0)
R(t)=∫−∞∞u(t)
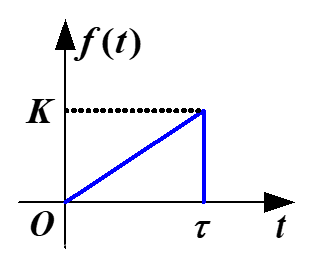
三角脉冲信号
f(t)={τKR(t) (0⩽t⩽τ)0 (other)
单位冲激信号
单位冲激信号的定义及图像
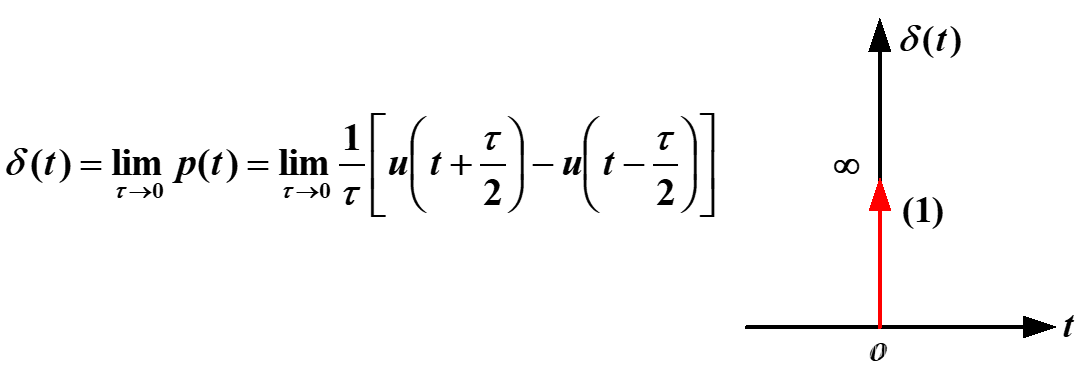
冲激函数的性质
- 冲激函数与单位阶跃函数的关系:
∫−∞tδ(τ)dτ=u(t),δ(t)=dtdu(t)
- 抽样性:
∫−∞∞f(t)δ(t−t0)dt=f(t0)
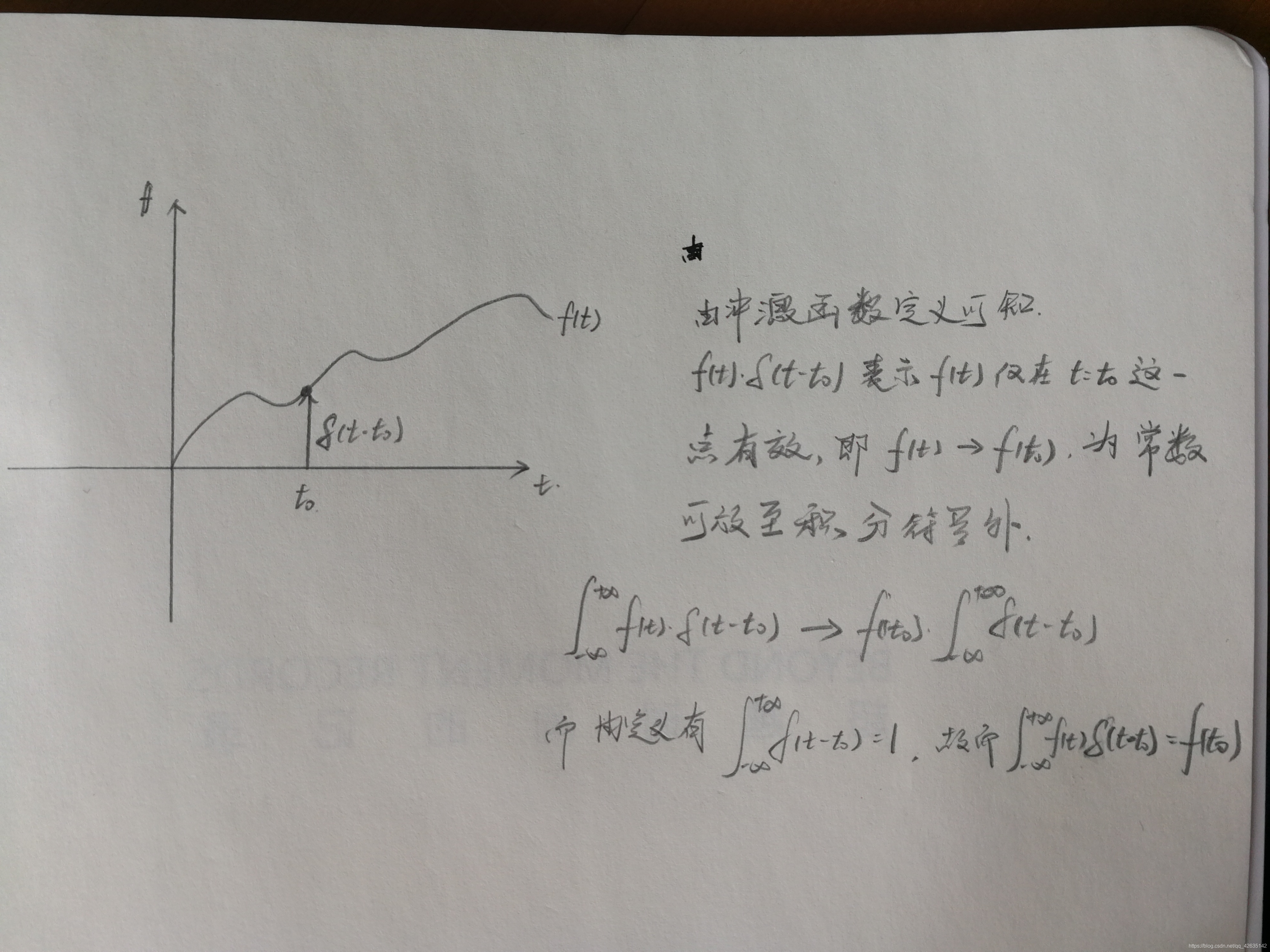
- 奇偶性:为偶函数,
δ(−t)=δ(t)
- 尺度变换性质:

(这里
a和
t0为常数,且
a̸=0)
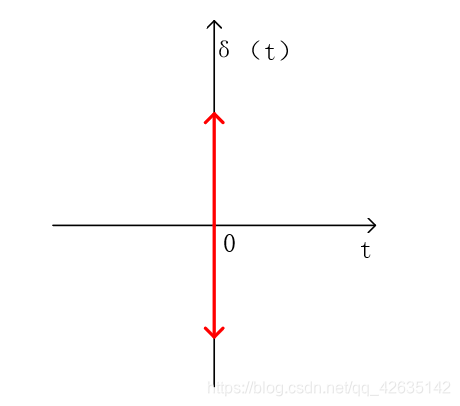
冲激偶信号——冲激函数的导数
冲激偶信号的定义和图像
冲激函数的微分,呈现正负极性的一对冲激,称为冲激偶信号
图像如下:
冲激偶的性质
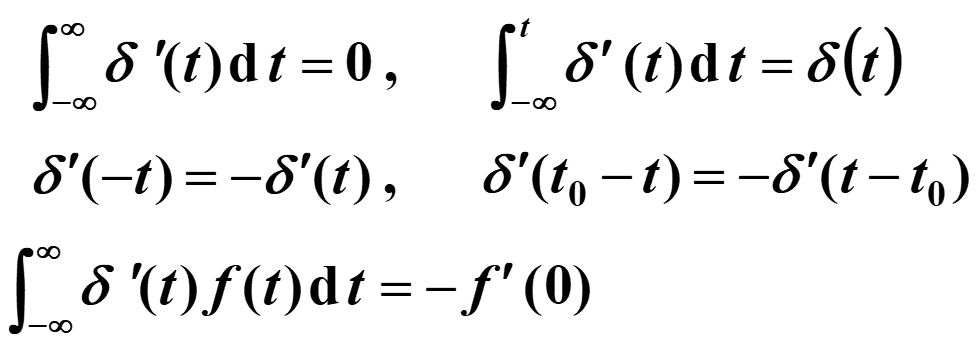
信号的分解
信号从不同角度分解:
- 直流分量与交流分量
- 偶分量与奇分量
- 脉冲分量
- 实部分量与虚部分量
- 正交函数分量
- 利用分形理论描述信号
直流分量与交流分量
f(t)→fD(t)+fA(t)
fD(t)为信号直流分量,
fA(t)为交流分量
信号的直流分量值的是信号的平均值
偶分量与奇分量
数学中,任何一个函数可以分解为偶函数和奇函数,信号也是如此
f(t)→fe(t)+fo(t)
fe(t)为信号偶分量,
fo(t)为奇分量
分解方法:
- 判断信号是否为单纯的偶信号或者是奇信号
- 若不是,则可先将信号反褶,即
f(t)→f(−t)
- 利用
fe=21[f(t)+f(−t)]和
fo=21[f(t)−f(−t)]对信号进行分解
脉冲分量
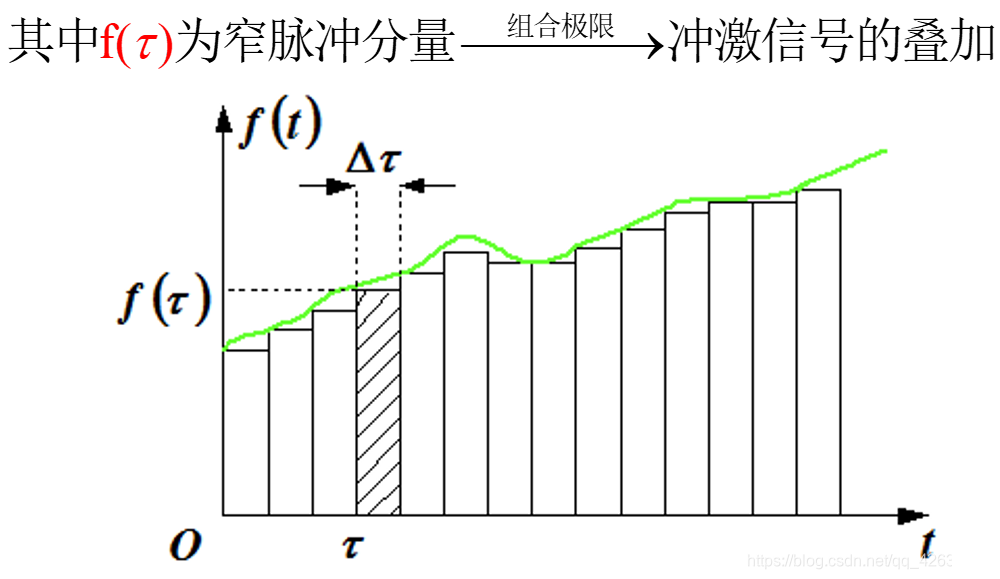
脉高:
f(τ)
脉宽:
Δτ
存在区间:
u(t−τ)−u(t−τ−Δτ)
此脉冲可表示为:
f(τ)[u(t−τ)−u(t−τ−Δτ)]
实部分量与虚部分量
对于瞬时值为复数的信号f(t)可分解为实、虚部两个部分之和
f(t)→fr(t)+jfi(t)
其实部为:
fr(t)=21[f(t)+f∗(t)]
虚部为:
jfi(t)=21[f(t)−f∗(t)]
系统模型及分类
连续系统与离散系统
输入和输出均为连续时间信号的系统称为连续时间系统。
输入和输出均为离散时间信号的系统称为离散时间系统。
连续时间系统的数学模型是用微分方程来描述,而离散时间系统的数学模型是用差分方程来描述。
动态系统与即时系统
若系统在任一时刻的响应不仅与该时刻的激励有关,而且与它过去的历史状况有关,则称为动态系统或记忆系统。
判别方法:
含有记忆元件(电容、电感等)的系统是动态系统。否则称即时系统或无记忆系统。
线性系统与非线性系统
能同时满足齐次性与叠加性的系统称为线性系统。满足叠加性是线性系统的必要条件。不能同时满足齐次性与叠加性的系统称为非线性系统。
判别方法:
若有激励
e(t),响应
r(t),之间满足
r(t)=F[e(t)]
- 齐次性: 若
F[ae(t)]=aF[e(t)],则说明该系统有齐次性
- 可加性: 若
F[e1(t)+e2(t)]=F[e1(t)]+F[e2(t)],则说明该系统有可加性
在判别线性系统的时候,齐次性可加性需同时满足,故可一起判别:
若
F[C1e1(t)+C2e2(t)]=C1F[e1(t)]+C2F[e2(t)],则说明该系统是线性系统
时不变系统与时变系统
时不变性质: 若系统满足输入延迟多少时间,其激励引起的响应也延迟多少时间
判别方法:
- 有激励
e(t),响应
r(t),之间满足
r(t)=F[e(t)],若输入延迟
t0个单位时间长度,即
e(t−t0),若有响应
r(t−t0),则说明该系统为时不变系统,反正则为时变系统
- 直观判断方法:若
e(t)前出现变系数,或有反转、展缩变换,则系统为时变系统
因果系统与非因果系统
激励引起的响应仅与该时刻之前的激励有关,即该系统无法预见未来。也可理解为响应与未来输入有关。
判别方法:
有激励
e(t),响应
r(t),之间满足
r(t)=F[e(t)],给出某一时刻激励有
r(t0)=e(t1),若
t1>t0说明响应在激励之前,也就是相应遇见了未来的激励,所以该系统为非因果系统,否则为因果系统
稳定系统与不稳定系统
若对有界的激励
e(t),产生的响应
r(t)也是有界时,则称该系统为有界输入有界输出稳定,简称稳定。
可逆与不可逆系统
- 如果已知可逆系统的输出,就可计算其唯一的输入
- 原系统与其可逆系统就构成一个恒等系统
例如:
-
r(t)=dtde(t)是不可逆系统,因为
∫dtde(t)的结果不唯一
-
r(t)=∫−∞te(τ)dτ是可逆系统,因为
dtd∫−∞te(τ)dτ的结果唯一
系统的描述
- 描述连续动态系统的数学模型是微分方程
- 描述离散动态系统的数学模型是差分方程
- 解析描述——建立数学模型
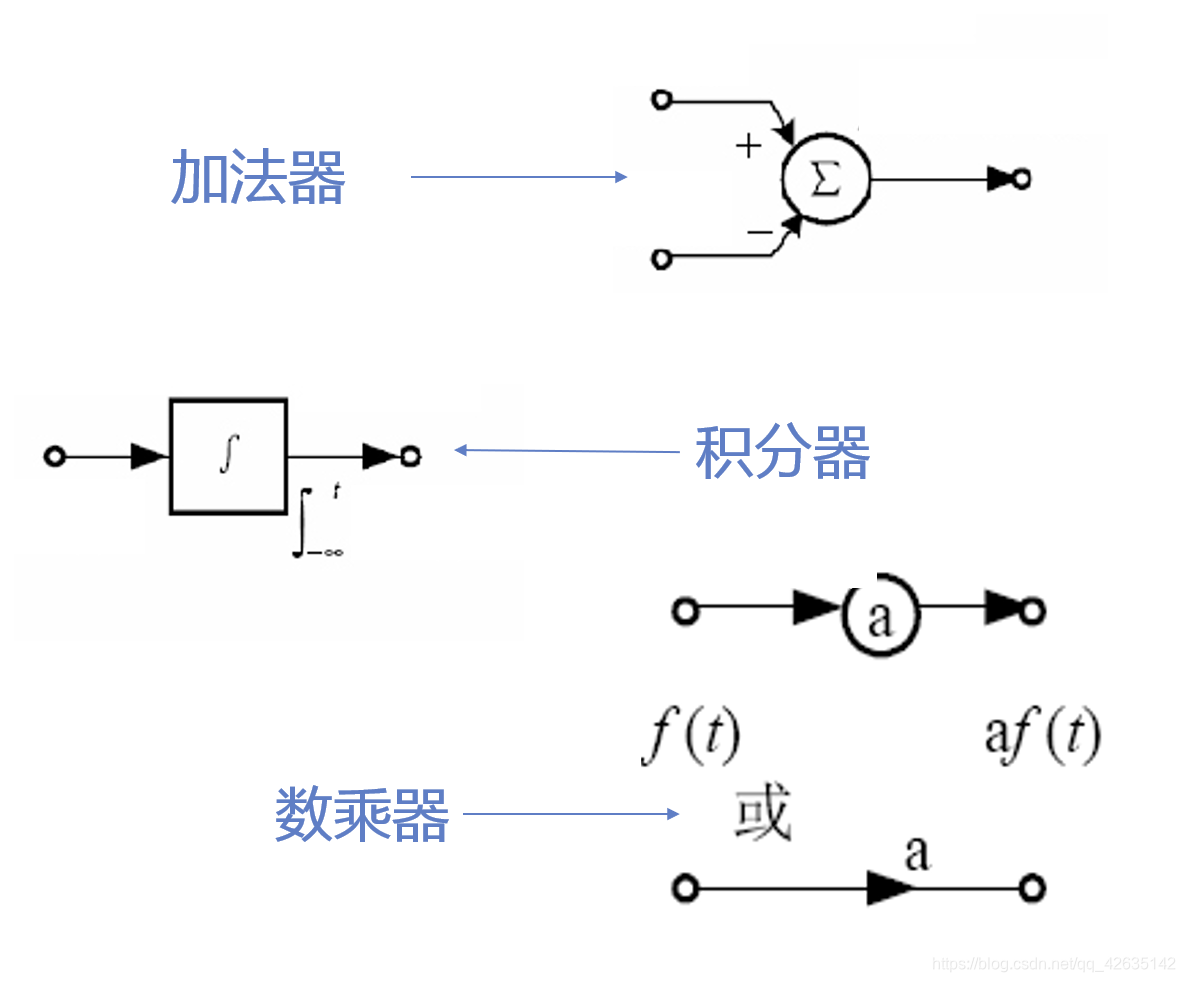
- 系统的框图描述