1. 龙伯格状态观测器概念

已经线性系统模型如下：

$\left\{\begin{matrix} \dot{x}=Ax+Bu\\ y=Cx \end{matrix}\right.$

当系统状态量难以获取，但实际控制中又需要利用系统状态量时，如何通过输入量和输出量重构系统状态量？这便是龙伯格状态观测器设计初衷，将实现系统状态的系统称为状态观测器。

为确保估计状态 $\tilde{x(t)}$ 逼近系统真实状态 $x(t)$ ，需满足如下条件：

$\lim_{t \to\propto }\left [{ \tilde x(t)-x(t)} \right ]=0$

其中， $\tilde{x(t)}$ 称为 $x(t)$ 的重构状态或者状态估计值。

2. 状态观测器设计

假设系统状态观测量和输出观测量满足如下方程：

$\left\{\begin{matrix} \dot{\tilde{x}}=A\tilde{x}+Bu\\ \tilde{y}=C\tilde{x} \end{matrix}\right.$

龙伯格状态观测器模型：

$\dot{\tilde{x}}=A\tilde{x}+Bu+L(y-C\tilde{x}) =(A-LC)\tilde{x}+Bu+Ly$

其中，A为状态矩阵，B为输入矩阵，C为输出矩阵，L为观测器增益矩阵，对偏差的加权。

（1）状态估计的开环处理

若采用开环控制实现状态估计，其系统结构如图1所示，该系统模型简单，但存在模型不确定性和扰动，初始状态未知等问题。

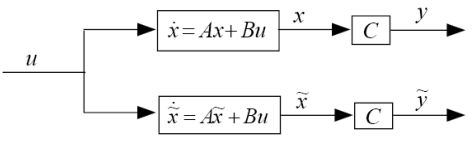
图1 基于开环控制的状态观测器实现

（2）状态估计的闭环处理

为提高系统的抗干扰性能，故采用闭环控制来实现状态估计，根据输出误差控制状态误差，使得估计状态和真实状态之间的误差逐步减小，其系统结构图如图2所示。

图2 基于闭环控制的状态观测器实现

定义真实状态和估计状态的误差向量如下：

$e=x-\tilde{x}$

则误差的动态行为为：

$\dot{e}=\dot{x}-\dot{\tilde{x}} \\ =Ax+Bu-(A-LC)\tilde{x}-Bu-Ly \\=Ax-(A-LC)\tilde{x}-LCx =(A-LC)e$

由上式可知，矩阵(A-LC)的极点决定了误差是否衰减以及如何衰减，而对于一个已知系统，A和C由系统特性决定。因此，增益矩阵L成为系统是否稳定的关键，这一问题被成为系统的极点配置问题。若能使得矩阵 A － LC 具有适当的特征值，则可以使得误差具有一定的衰减率。

由于

$det\left [ \lambda I-(A-LC) \right ]=det\left [ \lambda I-(A-LC)^{T} \right ]=det\left [ \lambda I-(A^{T}-C^{T}L^{T})\right ]$

因此，问题转化为 $\left ( A^{T},C^{T}\right )$ 的极点配置问题，该极点配置问题可解的充要条件为：

$\left ( A^{T},C^{T}\right )$ 完全能控 $\Leftrightarrow$ $\left ( C,A\right )$ 完全能观

观测器的增益矩阵可以按照极点配置方法来设计求解 $\left ( A^{T},C^{T}\right )$ 的极点配置问题，得到增益矩阵K；观测器增益矩阵 $L=K^{T}$ 。观测器设计的三种方法：直接法、变换法、爱克曼公式。

3. 状态观测器实例

考虑由以下系数矩阵给定的系统

$A=\begin{bmatrix} 1 & 1\\ -1&0 \end{bmatrix}$ ， $B=\begin{bmatrix} 1\\ 0 \end{bmatrix}$ ， $C=\begin{bmatrix} 1 & 0 \end{bmatrix}$

设计一个观测器，使观测器两个极点都是－2。

方法一：直接法

解：（1）检验系统的能观性：

$\tau _{0}=\begin{bmatrix} C\\ CA \end{bmatrix}=\begin{bmatrix} 1 & 0\\ 0& 1 \end{bmatrix}$

系统是能观的，因此问题可解。

(2) 要求确定观测器增益矩阵 $L=\begin{bmatrix} l_{1}\\ l_{2} \end{bmatrix}$ ，使得矩阵 $A-LC$ 具有两个相同的特征值－2。由于

$det[\lambda I-(A-LC)]=det\left ( \begin{bmatrix} \lambda & 0\\ 0&\lambda \end{bmatrix} -\begin{bmatrix} 0 &1 \\ -1&0 \end{bmatrix}+\begin{bmatrix} l_{1}\\ l_{2} \end{bmatrix}\begin{bmatrix} 1 & 0 \end{bmatrix}\right ) \\ =det\left ( \begin{bmatrix} \lambda + l_{1} &-1 \\ 1+l_{2}& \lambda \end{bmatrix} \right ) \\ =\lambda ^{2}+l_{1}\lambda +1+l_{2}$

(3)期望的特征值多项式是

$\left ( \lambda +2 \right )\left ( \lambda +2 \right )=\lambda ^{2}+4\lambda +4$

比较两个多项式，可以得到，

$l_{1}=4, l_{2}=3 \Rightarrow L=\begin{bmatrix} 4\\ 3 \end{bmatrix}$

所求的观测器是

$\dot{\tilde{x}}=(A-LC)\tilde{x}+Bu+Ly=\begin{bmatrix} -4 &1 \\ -4& 0 \end{bmatrix}\tilde{x}+\begin{bmatrix} 1\\ 0 \end{bmatrix}u+\begin{bmatrix} 4\\ 3 \end{bmatrix}y$

方法二：爱克曼公式

%% 利用MATLAB中的acker函数求解状态观测器
% 作者：Peng Jin
% 时间：2019年2月19日
%%
clc
clear all
close all

% 系统矩阵
A = [0 1; -1,0];
B = [1;0];
C = [1 0];

% 期望的极点
P = [-2;-2];

% 判断系统是否完全能观
E_obs = obsv(A,C);           % 求解能观性矩阵
E_val = rank(E_obs);         % 根据能控性矩阵是否满秩判断能观性

L_acker = (acker(A',C',P))';  % 利用acker求状态增益矩阵L

路漫求索_CUMT

发布了56 篇原创文章 · 获赞 50 · 访问量 11万+

私信关注

故障诊断4—龙伯格状态观测器设计