树(Tree)是n(n>=0)个结点的有限集。
在任意一棵非空树中:
(1)有且仅有一个特定的称为根(Root)的结点;
(2)当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,...,Tn,其中每个集合本身又是一棵树,并称为根的子树(SubTree)
森林:n棵互不相交的树
二叉树:度最多为2的树
二叉树特点:1>n0 = n2 + 1
2>非空二叉树上第k层上至多有个结点(k >= 1)
3>高度为H的二叉树至多有个结点(H >=1)
满二叉树:对于一棵高度为H的二叉树,将含有个结点的二叉树称为满二叉树
满二叉树特点:满二叉树只有最下面一层含有叶结点,并且除了叶结点外每个结点的度均为2,第i层(1<= i =< H-1)上结点的个数为
完全二叉树:与满二叉树相比,第H层从右边开始连续缺失若干个叶结点,这样的二叉树称为完全二叉树。满二叉树是完全二叉树的特例。
完全二叉树特点:叶结点只可能在层次最大的两层上出现,且最下层的叶结点都集中在左边连续的位置;如果有度为1的结点,只可能有一个,且该结点只有左孩子。
二叉排序树(二叉查找树,BST):左子树结点值 <= 根结点值 =< 右子树结点值
二叉排序树特点:1>若左子树非空,则左子树上所有结点关键字值均不大于根结点的关键字值
2>若右子树非空,则右子树上所有结点关键字值均不小于根结点的关键字值
3>左、右子树本身也是一棵二叉排序树。进行中序遍历的时候可以得到一个非递减的有序序列。
二叉平衡树(AVL树):左右子树的高度差(平衡因子,BF)为-1、0或1
如何调整二叉树成为平衡二叉树:1>LL平衡旋转(右单旋转):
(操作)在结点A的左孩子(L)的左子树(L)上插入新结点,以A为根的子树失去平衡
(调整)将A的左孩子B向右上旋转代替A成为根结点,A结点向右下旋转成为B的右子树的 根结点
2>RR平衡旋转(左单旋转):
(操作)在结点A的右孩子(R)的右子树(R)上插入新结点,以A为根的子树失去平衡
(调整)将A的右孩子B向左上旋转代替A成为根结点,A结点向左下旋转成为B的左子树的 根结点
3>LR平衡旋转(先左后右旋转):
(操作)在结点A的左孩子(L)的右子树(R)上插入新结点,以A为根的子树失去平衡
(调整)将A的左孩子B的右子树的根结点C向左上旋转至B的位置,然后再把C向右上旋转 至A的位置
3>RL平衡旋转(先右后左旋转):
(操作)在结点A的右孩子(R)的左子树(L)上插入新结点,以A为根的子树失去平衡
(调整)将A的右孩子B的左子树的根结点C向右上旋转至B的位置,然后再把C向左上旋转 至A的位置
哈夫曼树(Huffman):在含有N个结点的带权二叉树中,带权路径长度WPL最小的二叉树成为哈夫曼树,也称为最优二叉树。
哈夫曼树的构造过程:1>将这N个结点分别作为N棵仅含一个结点的二叉树,构成森林F
2>构造一个新结点,并从F中选取两棵根结点权值最小的树作为新结点的左右子树,并且将新结点的权值 置为左右子树上根结点的权值之和
3>从F中删除刚才选中的两棵树,同时将新得到的树加入F中
4>重复步骤2,3,直至F中只剩下一棵树为止
哈夫曼树的特点:1>每个初始结点最终都成为叶结点,并且权值越小的结点到根结点的路径长度越大
2>构造过程中共新建了N-1个结点,因此哈夫曼树中结点总数为2N-1
树中每个节点表示表中的一个记录,节点里的值为该记录在表中的位置,通常称这个折半查找过程的二叉树为折半判定树。
二叉判定树的节点是各个元素的下标或在表中的位置。比如有一个文件【11,22,33,44,55,66】,我想查找44是否在该文件中,利用折半查找的思想,可以将此文件构造成一个二叉判定树。

根节点是3,注意二叉判定树的节点是下标或位置,这里不能写33。
折半判定树的构造方法:1>当n=0时,折半查找判定树为空;
2>当n>0时,折半查找判定树的根结点为mid=(n+1)/2,
根结点的左子树是与有序表r[1] ~ r[mid-1]相对应的折半查找判定树,
根结点的右子树是与r[mid+1] ~ r[n]相对应的折半查找判定树。
折半判定树的特点:1>任意两棵折半查找判定树,若它们的结点个数相同,则它们的结构完全相同
2>具有n个结点的折半查找树的高度为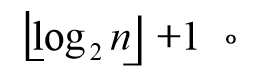
折半判定树的性质: 1>任意结点的左右子树中结点个数最多相差1
2>任意结点的左右子树的高度最多相差1
3>任意两个叶子所处的层次最多相差1
