【数据结构】树

1，概念

树的使用场景：有序或彼此之间有联系的一组数据。
结点的度：结点拥有的子树数。
堂兄弟：双亲在同一层结点。
层次：根为第一层，树的最大层次就是树的深度或高度。

2，二叉树

1）性质

性质1：二叉树的第i层至多有2^(i-1)个结点
性质2：深度为k的二叉树至多有（2^k）-1个结点。
性质3：若叶子结点为n0，度为2的结点数为n2，则n0 = n2 + 1

对于结点总数n,度为1的结点数n1，有：    n =  n0 + n1 + n2
算叶子结点角度出发：              n = n1 + 2n2 + 1
以上推出性质3.

性质4：具有n个结点的完全二叉树的深度为 logn + 1 （log n向下取整）
性质5：n个结点，按层序编号，对任一结点 i ：
如果 i =1，则结点是根。
如果 i >1，则其双亲结点为 i/2 （向下取整）
如果 2i > n，则 i 无左孩子；否则其左孩子为结点 2i .
如果 2i + 1 > n，则 i 无右孩子；否则其右孩子为 2i+1 .

 由于根节点是从0开始存储，因此父节点 i 的左孩子为 2*i+1，右孩子为 2*i+2。
    故当孩子节点为k时要分情况讨论，此时设父节点为x 
    1,k为左孩子 
        2*x+1=k 解得：x=(k-1)/2 

    2,k为右孩子 
        2*x+2=k 解得：x=(k-2)/2 

总体来说，此时根节点必为x=(k-1)/2(向下取整）

2）存储结构

①顺序存储

存储单元自上而下，自左至右一次存储完全二叉树的结点元素。（0表示不存在此结点）

②链式存储

二叉链表

含有两个指针域：结点、lchild、rchild

n个节点的二叉树有2n个链域，除了根节点没有被lchild和rchild指向,其余的节点必然会被指到.所以
空指针共有**2n-(n-1)=**n+1;
非空指针有**2n-(n+1)=**n-1；

三叉链表

含有三个指针域：结点、lchild、rchild、parent

线索链表和线索二叉树

线索二叉树结点结构：

其中：

ltag=0 时lchild指向左孩子；
ltag=1 时lchild指向前驱；
rtag=0 时rchild指向右孩子；
rtag=1 时rchild指向后继；

以这种结点结构构成的二叉链表作为二叉树的存储结构，叫做线索链表；二叉树为线索二叉树。
建立线索二叉树，或者说对二叉树线索化，实质上就是遍历一棵二叉树。所以又有先序线索二叉树、中序……、后序……

简而言之，就是把树中原本的null指针利用起来，分别指向它的前驱结点和后继结点。如下图：

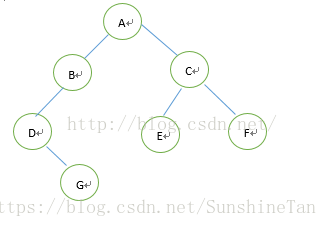
上面这棵树中序遍历为：DGBAECF。其线索二叉树为：

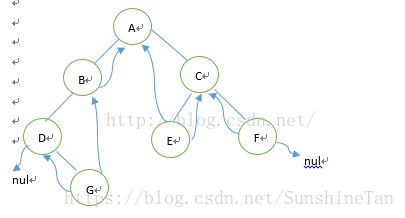
有了线索二叉树后，对它进行遍历时，其实就等于操作一个双向链表结构。
这样的好处是：我们既可以从第一个结点起顺后继进行遍历，也可以从最后一个结点起顺前驱进行遍历。方便我们对结点进行增删操作。
注意：对于后续遍历（左右中），最后访问的是子树的根节点，而子树根节点的两个指针域都指向子树了，所以不能空出来存放线索信息。故后序线索二叉树找后继需要知道双亲，即需带标志域的三叉链表作为存储结构。

3，树

1）存储结构

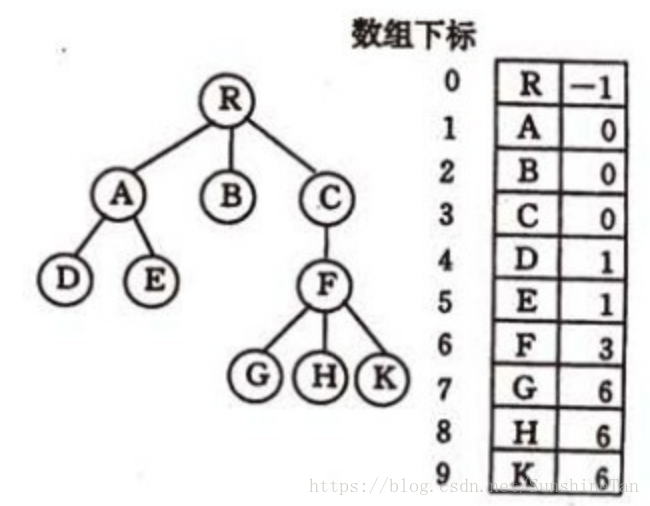
①双亲表示法（父亲数组表示法、父链表示法）

data、parent（指向双亲结点）
以一组连续空间存储树。
缺点：求结点的孩子时遍历整个结构。

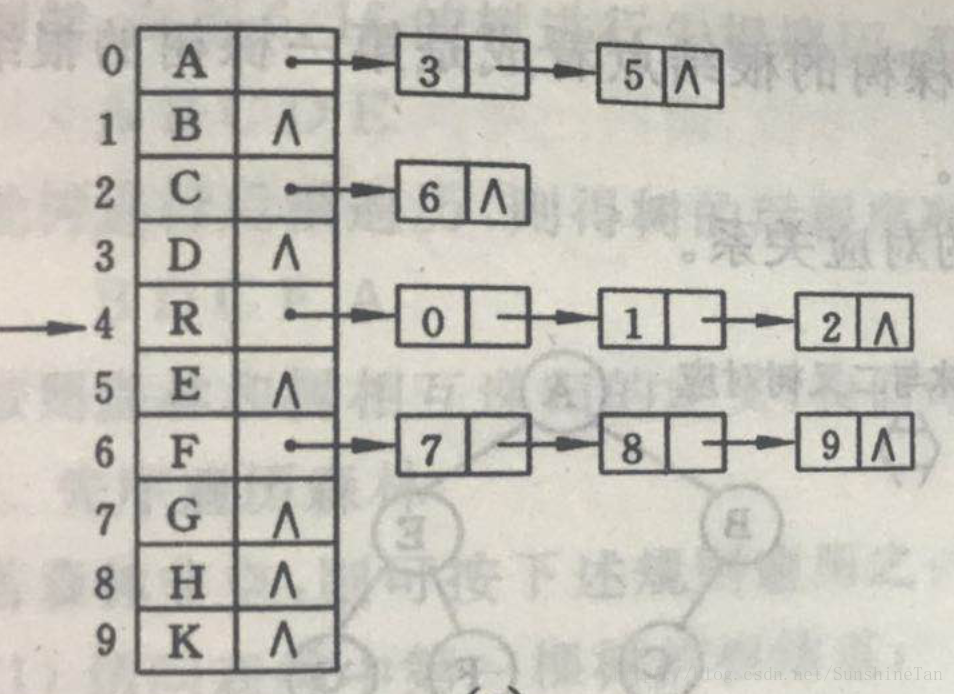
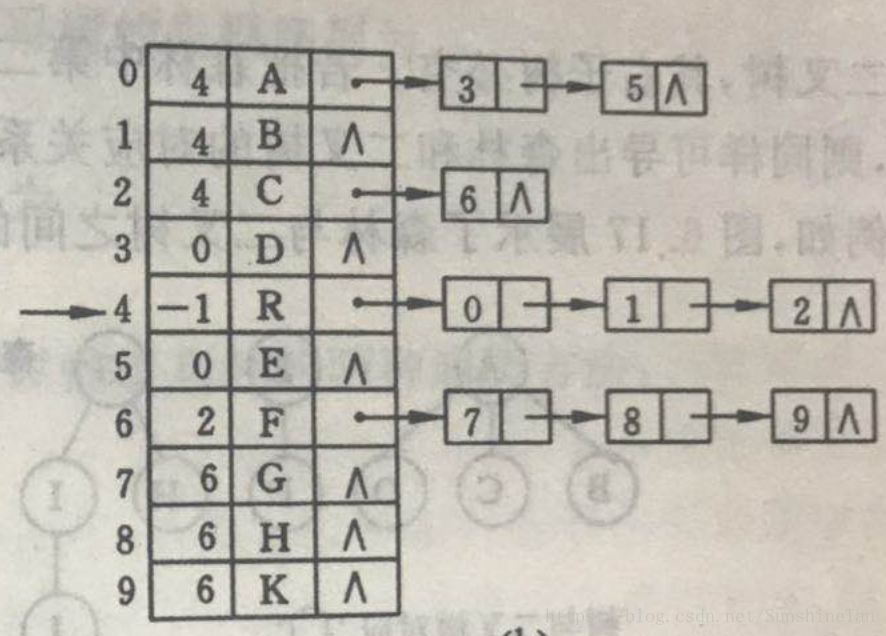
②孩子表示法（儿子链表表示法）

多重链表（多个指针域指向孩子们：data child1 child2 ……）：这样有多个空指针域。
改进：data degree child1 ……childd ( child指针有degree个，节省空间，单身不方便操作）

③孩子兄弟表示法（左儿子右兄弟二叉树表示法）

data *firstchild（第一个孩子） *nextsibling（下一个兄弟）

2）森林和二叉树的转换

森林转换为二叉树

对于森林F，二叉树B。
F为空，则B为空树；
若F非空，B的根为F第一棵树的根，F的孩子放在新结点的左子树，F的兄弟为右子树。

森林的第二棵树可以是根结点的右子树。

综上所述，任何一颗树树对应的二叉树，其右子树必为空。

对于有序树转换为二叉树：树的后序遍历 == 二叉树的中序遍历；树的前序遍历 == 二叉树的前序遍历。

二叉树转换为森林

森林转换二叉树逆向即可。

计算

已知一棵有2011 个结点的树，其叶结点个数为 116，该树对应的二叉树中无右孩子的结点的个数是（ ）。
解析：
树——>二叉树，大孩子变左孩子，兄弟变右孩子
因此对应的二叉树没有右孩子，说明该结点在树里右边没有兄弟，也就是说，该结点是其父结点最右边的孩子。有多少个有孩子的节点，就有多少个“最右的孩子节点”，因此2011-116=1895

3）多叉树性质

1） 结点总数计算
结点总数（包括根和叶子） = 边数 + 1。
如：在一棵三元树中度为3的结点数为2个,度为2的结点数为1个,度为1的结点数为2个,则度为0的结点数为()个
这里边数 = 3*2+2+2= 10 结点总数为11 减去度不为0的结点：11-2-1-2=6 即为叶结点

5，最小生成树（贪心算法）

1）单源最短路径（Dijkstra算法）

①概念

Dijkstra算法解决的是带权重的有向图上单源最短路径问题，该算法要求所有边的权重都为非负值。
Dijkstra不能为负权，因为算法中使用了优先队列和BFS思想，若有负权，则先出队列的可能并不是全局路径最短的，因为后面可能还有负值更大（即更短的路径），比如求(a, c)路径，有路径a -> b (-10)-> c(-10)，则为-20时，c出队列，而有另外路径a -> d(1) -> c(100)，d的权为1因此出不了队列，后面(d,c)为-100的权就无法在c出队列之前更新c了，因此造成最短路径为(a,b,c)，实际上最短路径为(a,d,c)。

②基本思想

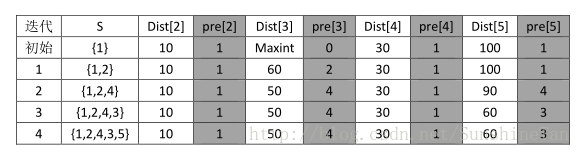
顶点集合S中，仅含有源。用dist[i]记录每个顶点u[i]与源的最短路径长度(没有路径记为无穷大）。
从dist中选出第i个节点为最短路径，则在S中加入顶点u，并对dist大小做修改（每个顶点与源的最短路径，可以经过新加入的结点）
一旦S包含了所有V中顶点，dist就记录了从源到所有其他顶点直接的最短路径长度。

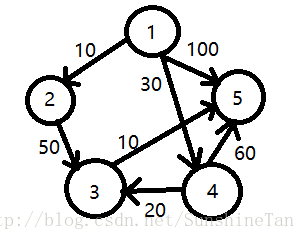
如果还要求出相应的最短路径，则增加prev数组，记录最短路径上i的前一个顶点。

③复杂度

Dijkstra算法解决了从某个原点到其余各顶点的最短路径问题，由循环嵌套可知该算法的时间复杂度为O(N*N)。
若要求任一顶点到其余所有顶点的最短路径，一个比较简单的方法是对每个顶点当做源点运行一次该算法，等于在原有算法的基础上，再来一次循环，此时整个算法的复杂度舅变成了O(N*N*N)。
（3）

2）最小生成树（Prim算法、Kruskal算法）

连通图才有生成树，分为深度优先生成树和广度优先生成树 2.非连通图是生成森林。

①场景

设计通信网络，建立城市之间的通信线路。

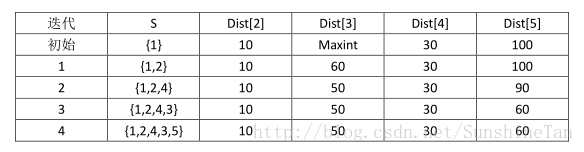
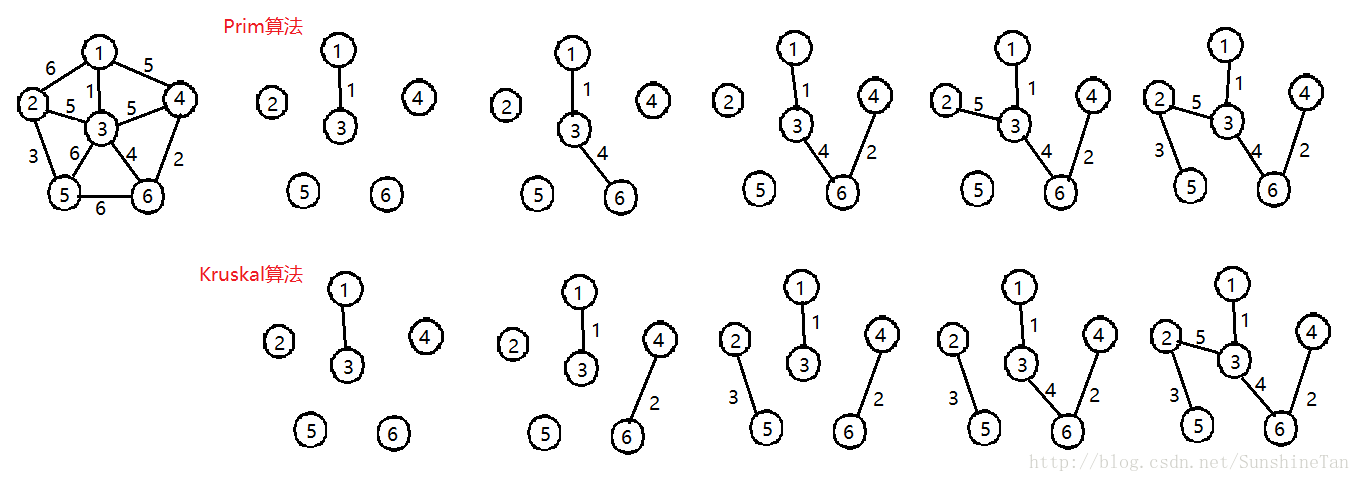
②prim算法贪心选择

顶点集S={1}，选取与顶点集中各顶点边最小的顶点，加入顶点集S。重复迭代上述步骤。

③kruskal算法贪心选择

①按边的权值从小到大排序。
②由小到大取边（直到生成n-1条边为止。注意：取边时，两个顶点分别在不同的连通分支上。）

6，二叉树应用

1）平衡二叉树（Balanced Binary Tree、AVL树） （重要）

①概念

它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

②作用

插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能（O（log（n）））。

③常用实现方法

a.红黑树（ R-B Tree，Red Black Tree，平衡二叉B树） （重要）

红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。

红黑树的特性:
（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

注意：
① 特性(3)中的叶子节点，是只为空(NIL或null)的节点。
② 特性(5)，确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树。

nil：指向oc中对象的空指针。
Nil：指向oc中类的空指针。
NULL：指向其他类型的空指针，如一个c类型的内存指针。

红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率非常之高。如，需要使用动态规则的防火墙系统，使用红黑树而不是散列表被实践证明具有更好的伸缩性。

典型的用途是实现关联数组
例如，Java集合中的TreeSet和TreeMap，C++ STL中的set、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。

b.AVL

c.替罪羊树

d.Treap

e.伸展树

2）二叉排序树（BST，Binary Sort Tree，二叉查找树，二叉搜索树）

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉搜索树。
二叉查找树性质：对二叉查找树进行中序遍历，即可得到有序的数列。

①查找

复杂度：
和二分查找一样，插入和查找的时间复杂度均为O(logn)，
最坏情况下复杂度为：O(n) （二分查找最坏情况下复杂度为log2(n+1)；原因在于插入和删除元素的时候，树没有保持平衡（如一棵树所有结点只有左子树））

②插入新数

插入的结点一定是叶子结点。插入后需要重新调整平衡性。

③平衡性

平衡因子：某一个结点 左子树高度 - 右子树高度。

若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
平衡性调整：
首先要找出插入新结点后失去平衡的最小子树根结点的指针。然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树。

调整方式：

i>LL 型平衡旋转法

由于在 A 的左孩子 B 的左子树上插入结点 F ，使 A 的平衡因子由 1 增至 2 而失去平衡。故需进行一次顺时针旋转操作。 即将 A 的左孩子 B 向右上旋转代替 A 作为根结点， A 向右下旋转成为 B 的右子树的根结点。而原来 B 的右子树则变成 A 的左子树。

ii>RR 型平衡旋转法

由于在 A 的右孩子 C 的右子树上插入结点 F ，使 A 的平衡因子由 -1 减至 -2 而失去平衡。故需进行一次逆时针旋转操作。即将 A 的右孩子 C 向左上旋转代替 A 作为根结点， A 向左下旋转成为 C 的左子树的根结点。而原来 C 的左子树则变成 A 的右子树。

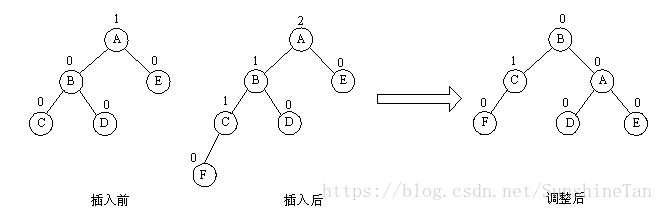
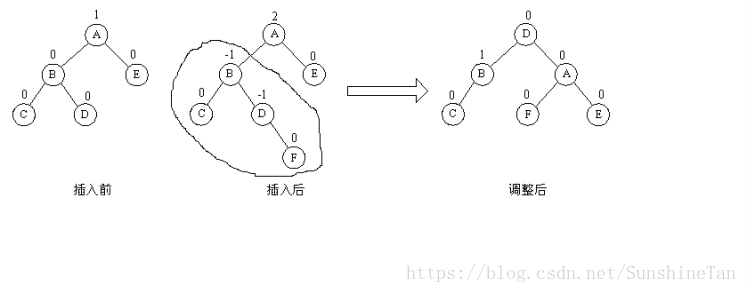
iii>LR 型平衡旋转法

由于在 A 的左孩子 B 的右子数上插入结点 F ，使 A 的平衡因子由 1 增至 2 而失去平衡。故需进行两次旋转操作（先逆时针，后顺时针）。即先将 A 结点的左孩子 B 的右子树的根结点 D 向左上旋转提升到 B 结点的位置，然后再把该 D 结点向右上旋转提升到 A 结点的位置。即先使之成为 LL 型，再按 LL 型处理 。

如图中所示，即先将圆圈部分先调整为平衡树，然后将其以根结点接到 A 的左子树上，此时成为 LL 型，再按 LL 型处理成平衡型。

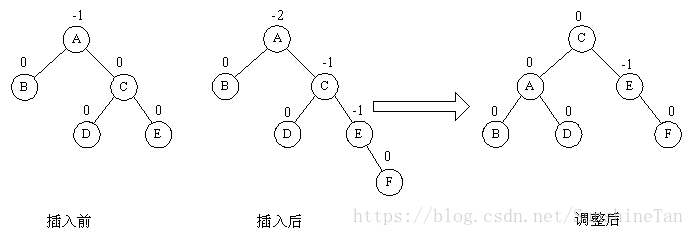
iv>RL 型平衡旋转法

由于在 A 的右孩子 C 的左子树上插入结点 F ，使 A 的平衡因子由 -1 减至 -2 而失去平衡。故需进行两次旋转操作（先顺时针，后逆时针），即先将 A 结点的右孩子 C 的左子树的根结点 D 向右上旋转提升到 C 结点的位置，然后再把该 D 结点向左上旋转提升到 A 结点的位置。即先使之成为 RR 型，再按 RR 型处理。

如图中所示，即先将圆圈部分先调整为平衡树，然后将其以根结点接到 A 的左子树上，此时成为 RR 型，再按 RR 型处理成平衡型。

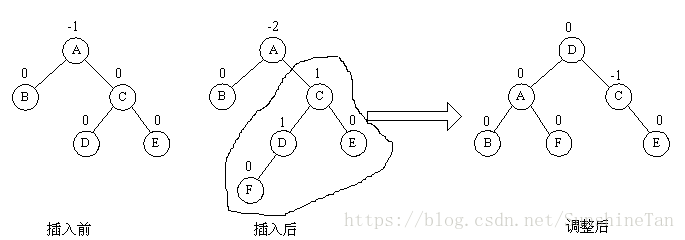
平衡化靠的是旋转。 参与旋转的是 3 个节点（其中一个可能是外部节点 NULL ），旋转就是把这 3 个节点转个位置。注意的是，左旋的时候 p->right 一定不为空，右旋的时候 p->left 一定不为空，这是显而易见的。

③键的检测序列

对任意结点，后面的值要么都大于它，要么都小于它。
如：
假设某棵二叉查找树的所有键均为1到10的整数，现在我们要查找5。2,8,6,3,7,4,5不可能是键的检查序列

④根据后序遍历识别是不是BST

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。
假设输入的数组的任意两个数字都互不相同。
思路：先找到右子树的开始位置，然后分别进行左右子树递归处理。
类似题目：根据前序遍历识别是不是BST

public boolean VerifySquenceOfBST(int[] sequence) {
        if (sequence == null || sequence.length == 0)
            return false;
        int rstart = 0;
        int length = sequence.length;
        for (int i = 0; i < length - 1; i++) {//BST中左子树结点小于根节点，找到左子树的开始位置
            if (sequence[i] < sequence[length - 1])//sequence[length - 1]为根节点
                rstart++;
        }
        if (rstart == 0) {//没有左子树
            VerifySquenceOfBST(Arrays.copyOfRange(sequence,0,length-1));
        }else {
            for (int i = rstart; i < length - 1; i++) {//BST中，右子树的结点大于根节点
                if (sequence[i] <= sequence[length - 1]) {
                    return false;
                }
            }
            //判断左子树是不是BST
            VerifySquenceOfBST(Arrays.copyOfRange(sequence,0,rstart));
            //判断右子树是不是BST
            VerifySquenceOfBST(Arrays.copyOfRange(sequence,rstart,length - 1));
        }
        return true;
    }

3）满二叉树

除最后一层无任何子节点外，每一层上的所有结点都有两个子结点二叉树。

4）完全二叉树

只有最下面的一层结点度能够小于2，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
堆是一种完全二叉树或者近似完全二叉树，所以效率极高。

5）B-树(B_树、B树、平衡的多叉树）

B-树是一种多路搜索树（并不一定是二叉的）。主要用作文件的索引。

①m阶B树定义：

一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。它或者是空树，或者是满足下列性质的树：
1、根结点至少有两个子女；
2、每个非根节点所包含的关键字个数 j 满足：┌m/2┐ - 1 <= j <= m - 1；（向上取整）
3、除根结点以外的所有结点（不包括叶子结点）的度数正好是关键字总数加1，故内部子树个数 k 满足：┌m/2┐ <= k <= m ；
4、所有的叶子结点都位于同一层。

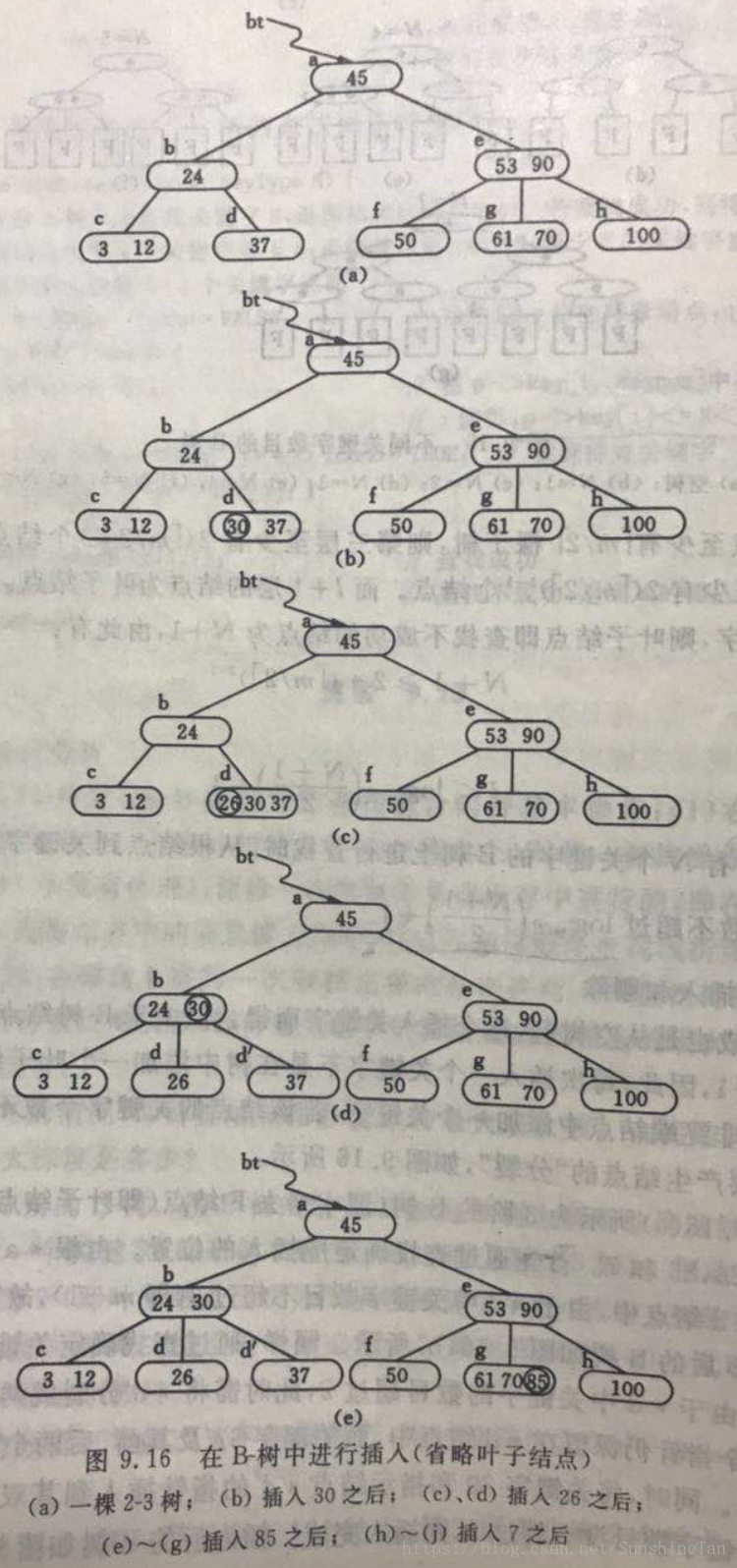
②查找

B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点。

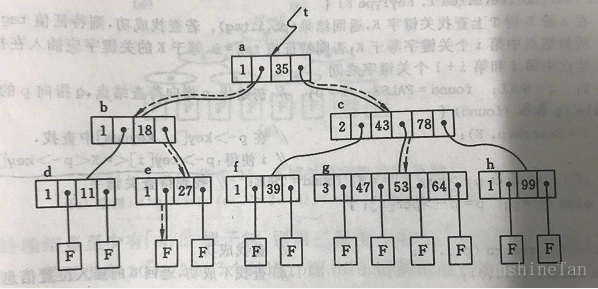
###③添加及删除结点

6）B+树（重要）

①概念

B-树的变形，为叶子结点增加链表指针（从大到小顺序链接）。
每个树上有2个头指针，一个指向根结点，另一个指向关键字最小的叶子结点。因此对B+树可以进行2种查找运算：一种是从最小关键字起顺序查找，另一种是从根结点开始随机查找。

②与B树区别

相同点：
B-树和B+树都是平衡的多叉树
B-树和B+树都可用于文件的索引结构
B-树和B+树都能有效地支持随机检索
不同点：
B+树在B树的基础上，为叶子结点增加了链表指针，能支持顺序检索。而B树不支持。

7）B*树

B+树的变形，为非叶子结点也增加链表指针。在B+树的非根和非叶子结点再增加指向兄弟的指针。

B树、B-树、B+树、B*树区别：
B-树（B树）：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；
B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；
B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；

8）Huffman树（最优树，哈夫曼树、霍夫曼树）

①基本思想（贪心算法）

将每一字符的频率放入队列Q。
从Q中取出具有最小频率的两棵树x和y，将它们合并为一颗新树。并把新书的频率放入队列Q中。
重复合并。合并n-1次后，优先队列中只剩下一棵树，即哈夫曼树。

②场景

给定带权路径长度最短的树。

定n个权值作为n个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

③应用

构造哈夫曼树并获取哈夫曼编码。
A,B,C,D,E五个字符，出现的频率（即权值）分别为5,4,3,2,1。构造过程如下：
1）取两个最小权值作为左右子树构造一个新树，即取D，E构成新树，其结点为1+2=3；
2）再从A,B,C,(DE)，取两个min数构成新树。
……
最后结果如图：

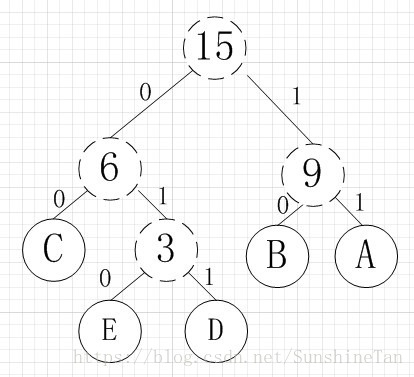
所以各字符对应的编码为：A->11,B->10,C->00,D->011,E->010
霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩，加密解密等场合。

WPL（带权路径长度） = 5*2 + 4*2 + 3*2 + 2*3 + 1 * 3 

④结点计算

哈弗曼树只有n0、n2结点。
如：一个215个结点的哈弗曼树，对其进行编码，有多少种不同的码字？
n0 = n2 + 1; n = n0 + n2. n0对应的是不同的编码。

9）笛卡尔树

笛卡尔树是一棵二叉树，树的每个节点有两个值，一个为key，一个为value。
i>对于key，笛卡尔树是一棵二叉搜索树，每个节点的左子树的key都比它小，右子树都比它大。
ii>对于value，所有结点的value满足优先队列（不妨设为最小堆）的顺序要求，即该结点的value值比其子树中所有结点的value值小。

10）键树（数字查找树, Trie树，字典树，前缀树，单词查找树）

①概念

是一颗度>=2的树，树中每个结点只含有组成关键字的符号。如：关键字是数值，则结点为一个数位；关键字是单词，结点为一个字母。

性质：
 - 根节点不包含字符，除根节点外每一个节点都只包含一个字符
 - 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串
 - 每个节点的所有子节点包含的字符都不相同

②场景

快速检索（最长前缀匹配），统计，排序和保存大量的字符串。
所以经常被搜索引擎系统用于文本词频统计，搜索提示等场景。它的优点是最大限度地减少无谓的字符串比较，查询效率比较高。

③主要思想

空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

④性能分析

每个节点的出度为m，高度为n。最坏空间复杂度为O(m^n)。
也正由于每个节点的出度为m，所以我们能够沿着树的一个个分支高效的向下逐个字符的查询，而不是遍历所有的字符串来查询，此时Trie树的最坏时间复杂度为O(n)。这正是空间换时间的体现，也是利用公共前缀降低查询时间开销的体现。

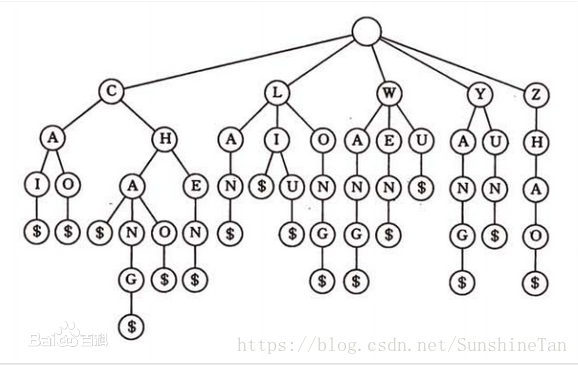
⑤举例

在ASC算法team日常开发中，常常面临一些数据结构的抉择，令人纠结。目前大家在策划一个FBI项目（Fast Binary Indexing），其中用到的词汇有6200条，词汇长度在10-15之间，词汇字符是英文字母，区分大小写。

使用TRIE树，检索最快。寻找子节点开销：1次运算/每字符

6，应用

1）二叉树的深度

二叉树高度最高的情况是每一个层只有一个结点，此时高度为N，
最小的情况是完全二叉树，高度是[log2N]+1，以2为底的对数取整后+1，
所以高度是[log2N]+1 到 N。

2）树的子结构

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）。
思路：如果A中有一部分子树的机构和B一样，那么B是A的子结构。
若根节点相等，利用递归比较他们的子树是否相等；若根节点不相等，则利用递归分别在左右子树中查找。

public class TreeNode{
        TreeNode left;
        TreeNode right;
        int val;
    }
    public boolean HasSubtree(TreeNode root1,TreeNode root2) {
        boolean result = false;
        if (root2 != null && root1 != null) {
            if(root1.val == root2.val){
                result = doesTree1HaveTree2(root1,root2);
            }
            if (!result)
                return HasSubtree(root1.left,root2) || HasSubtree(root1.right,root2);
        }
        return result;
    }
    public boolean doesTree1HaveTree2(TreeNode node1, TreeNode node2) {
        if (node2 == null) {
            return true;
        }
        if (node1 == null) {
            return false;
        }
        if (node1.val != node2.val) {
            return false;
        }
        return doesTree1HaveTree2(node1.left,node2.left) &&
                doesTree1HaveTree2(node1.right,node2.right);
    }

3）重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。
解题思路：根据前序遍历的第一个数字创建根节点；在中序遍历找到根节点的位置；确定左右子树节点数量；递归构建左右子树。

static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) { val = x; }
    }
    /**
     *
     * @param pre 前序遍历
     * @param in 中序遍历
     * @return
     */
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        if (pre == null || in == null) {
            return null;
        }
        if (pre.length == 0 || in.length == 0) {
            return null;
        }
        if (pre.length != in.length) {
            return null;
        }
        TreeNode root = new TreeNode(pre[0]);//根据前序遍历的第一个数字创建根节点
        for (int i = 0; i < pre.length; i++) {
            if (pre[0] == in[i]) {//中序遍历找到根节点的位置
                //确定左右子树
                root.left = reConstructBinaryTree(
                        Arrays.copyOfRange(pre,1,i+1),Arrays.copyOfRange(in,0,i));
                root.right = reConstructBinaryTree(
                        Arrays.copyOfRange(pre,i+1,pre.length),Arrays.copyOfRange(in,i+1,in.length));
            }
        }
        return root;
    }

4）二叉树的遍历

先序后序刚好相反，说明一个结点只有一个孩子，即二叉树的结点数等于高度。

①中序遍历

前缀表示（波兰式）

②先序遍历

中缀表示。

③后序遍历

后缀表示（逆波兰式）。算式的后缀表示可以唯一标志算式顺序，得到算式。
后序遍历有些结点是需要存储的，否则找不到，必须要用栈保存。

④广度优先遍历

需要一个辅助队列。

⑤深度优先遍历

需要一个辅助栈。

⑥代码

 /*
    * 前序遍历，递归实现
    * */
    public void PreOrder(TreeNode node) {
        if (node != null) {
            System.out.print(node.val);
            PreOrder(node.left);
            PreOrder(node.right);
        }
    }

    /*
    * 前序遍历，非递归实现
    * 1，先入栈根节点，输出根节点val值，再先后入栈其右节点、左结点；
    * 2，出栈左节点，输出其val值，再入栈该左节点的右节点、左节点；直到遍历完该左节点所在子树。
    * 3，再出栈右节点，输出其val值，再入栈该右节点的右节点、左节点；直到遍历完该右节点所在子树。
    * */
    public void PreOrder1(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        if (root != null) {
            stack.push(root);
        }
        while (!stack.empty()) {
            TreeNode node = stack.pop();
            System.out.print(node.val);
            //右结点先入栈，左结点后入栈
            if (node.right != null) stack.push(node.right);
            if (node.left != null) stack.push(node.left);
        }
    }
    /*
    * 中序遍历，递归实现
    * */
    public void InOrder(TreeNode node) {
        if (node != null) {
            InOrder(node.left);
            System.out.print(node.val);
            InOrder(node.right);
        }
    }

    /*
   * 中序遍历，非递归实现
   * 1，首先从根节点出发一路向左，入栈所有的左节点；
   * 2，出栈一个节点，输出该节点val值，查询该节点是否存在右节点，
   * 若存在则从该右节点出发一路向左入栈该右节点所在子树所有的左节点；
   * 3，若不存在右节点，则出栈下一个节点，输出节点val值，同步骤2操作；
   * 4，直到节点为null，且栈为空。
   * */
    public void InOrder1(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        while (root != null || !stack.empty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            if (!stack.empty()) {
                TreeNode node = stack.pop();
                System.out.print(node.val);
                root = node.right;
            }
        }
    }

    /*
    * 后序遍历，递归实现
    * */
    public void PostOrder(TreeNode node) {
        if (node != null) {
            PostOrder(node.left);
            PostOrder(node.right);
            System.out.print(node.val);
        }
    }

    /*
    * 层序遍历（广度优先遍历）
    * */
    public void LayerOrder(TreeNode root) {
        Queue<TreeNode> queue = new ArrayDeque<>();
        if (root != null) queue.offer(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.print(node.val);
            if (node.left != null) queue.offer(node.left);
            if (node.right != null) queue.offer(node.right);
        }
    }

5）二叉树的镜像

操作给定的二叉树，将其变换为源二叉树的镜像。
思路：使用递归或非递归方式交换每个节点的左右子树位置。
先序遍历树的每个结点，如果遍历的结点有子节点，则左右交换。当交换完所有的非叶子结点的左右子结点后，就得到了镜像术。

 public class TreeNode{
        TreeNode left;
        TreeNode right;
        int val;
    }
    public void Mirror(TreeNode root) {
        if (root == null) {
            return;
        }
        Stack<TreeNode> stack = new Stack<>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                TreeNode temp = root.left;
                root.left = root.right;
                root.right = temp;
                stack.push(root);
                root = root.left;
            }
            if (!stack.isEmpty()) {
                root = stack.pop();
                root = root.right;
            }
        }
    }

6）二叉树中和为某一值的路径

输入一颗二叉树和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结
点开始往下一直到叶结点所经过的结点形成一条路径。
思路：先保存根节点，然后分别递归在左右子树中找目标值，若找到即到达叶子节点，打印路径中的值。

   ArrayList<ArrayList<Integer>> resultList = new ArrayList<>();
    ArrayList<Integer> list = new ArrayList<>();
    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
        if(root == null)
            return resultList;
        list.add(root.val);
        target -= root.val;
        if(target == 0 && root.left == null && root.right == null){
            resultList.add(new ArrayList<>(list));
        }else {
            FindPath(root.left,target);
            FindPath(root.right,target);
        }
        //每返回上一层一次就要回退一个节点
        list.remove(list.size()-1);
        return resultList;
    }