红黑树是另一种自平衡二叉查找树。它通过较为复杂的调整,实现一种“局部平衡”。它的性能较为高效,应用广泛,被应用于linux内核进程调度,实现关联数组等。
本文将首先介绍红黑树的特点及其与AVL树的比较,然后说明红黑树的实现方式,评价红黑树的性能,最后对红黑树进行实践。
红黑树的特点
本节将整体介绍红黑树的特点,目的是探究红黑树的特点和优异之处。完全不了解红黑树的读者可以先跳过本节,在阅读完红黑树的实现之后再来阅读本节。
红黑树是一种自平衡的二叉查找树。它的实现机制非常复杂,所以一直困扰我的一个疑问是:为什么在逻辑简单的AVL树之后人们还要发明这样一种实现复杂的树,并且红黑树的应用比AVL树更为广泛?
AVL树是最早的一种自平衡二叉搜索树。如果说伸展树是为了节省AVL树节点中的height属性,那么红黑树,一棵这么复杂的树,的存在又是为了什么呢?
平衡二叉树的追求的是全局均衡,如在做插入,删除操作时,需要调整整棵树,显然这是费时的,因此希望在做调整时,是局部调整,因此提出了红黑树,这样一种高效的数据结构(也是最变态的一种数据结构)。
区别于严格平衡的AVL树,红黑树的自平衡是一种“局部平衡”——它只要求部分地达到平衡要求,降低了对旋转的要求,从而提高了性能。红黑树对以往的数据不会过多的调整,且可以保证任何不平衡在三次以内的旋转得到解决,红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高。
红黑树在删除时节点旋转次数是O(1),平衡因子调整次数是O(logn),而AVL树则两者都是O(logn)。红黑树和AVL树在插入时,节点旋转次数都是O(1),平衡因子调整次数都是O(logn)。
AVL树的删除
引自维基百科:
Let node X be the node which we have to delete, and let node Y be a node in the tree we need to find to take node X’s place, and let node Z be the actual node we take out of the tree.
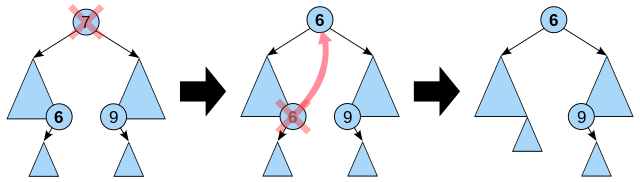
Steps to consider when deleting a node in an AVL tree are the following:
- If node X is a leaf or has only one child, skip to step 5 with Z:=X.
- Otherwise, determine node Y by finding the smallest[8] node in node X’s right subtree (the in-order successor of X − it does not have a left child) or the largest in its left subtree (the in-order predecessor of X − it does not have a right child).
- Exchange all the child and parent links of node X with those of node Y. In this step, the in-order sequence between nodes X and Y is temporarily disturbed, but the tree structure doesn’t change.
- Choose node Z to be all the child and parent links of old node Y = those of new node X.
- If node Z has a subtree (which then is a leaf), attach it to Z’s parent.
- If node Z was the root (its parent is null), update root.
- Delete node Z.
- Retrace the path back up the tree (starting with node Z’s parent) to the root, adjusting the balance factors as needed.
Since with a single deletion the height of an AVL subtree cannot decrease by more than one, the temporary balance factor of a node will be in the range from −2 to +2.
If the balance factor becomes ±2 then the subtree is unbalanced and needs to be rotated. The various cases of rotations are described in section Rebalancing.仔细研究rebalancing,我们可以发现,insertion下,旋转后与插入后子树的高度相同,而deletion下,旋转后树的高度会变化。所以删除的旋转可能会进行O(logN)次。
(在AVL Trees 学习笔记一文中,主要是根据上课的课件所做的整理,所以并没有考虑删除的情况。笔者目前暂时不对AVL树的插入、删除、旋转及其实现做详细的说明,若有需求可以参考维基百科中对AVL树的说明)
因此,在动态数据的方面,红黑树的表现要优于AVL树。这也是为什么红黑树被应用于linux内核进程调度、关联数组。
实现
定义
A red-black tree is a binary search tree that satisfies the following red-black properties:
- Every node is either red or **blac**k.
- The root is black.
- Every leaf (NIL) is black.
- If a node is red, then both its children are black.
- For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
插入
若在 黑节点 下插入,只需让插入节点为红色即可。
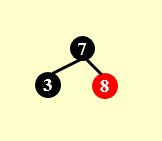
若在红节点下插入,而红节点没有sibling node,如在下图插入的“9”节点:
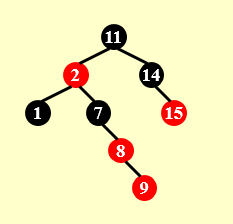
只需将7,8,9进行旋转,将其中的父节点置于黑色即可。
若红节点的sibling node是黑节点,我们可以证明这样的情况不存在因为这样这两个节点的父节点将违反第五条原则(For each node, all simple paths from the node to descendant leaves contain the same number of black nodes):
最后只剩下在红节点下插入节点,且红节点的兄弟节点为红节点,且它的父节点一定为黑色节点,也就是这样的情况:
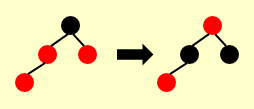
在这样的情况下,我们只需要将颜色变化即可。
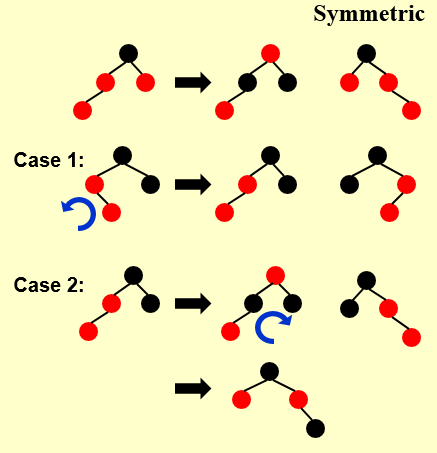
此时,若树遵循红黑树定义,则停止调整,但也有可能调整后会出现这样的情况:
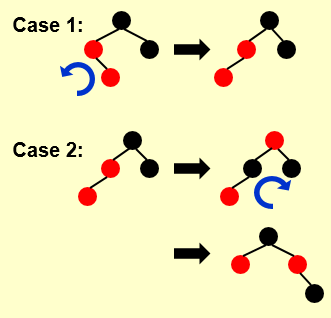
若是case1, 则我们将其通过旋转转换为case2,再继续进行调整。
首先变换颜色,然后再进行一次旋转,调整结束。
因为此时父节点为黑色,所以此时的树一定满足红黑树定义,不需要再进行调整。
通过上面的过程我们可以看到,红黑树的插入最多进行三次旋转。
对称的情况不予赘述。
插入的例子
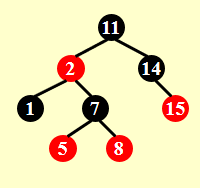
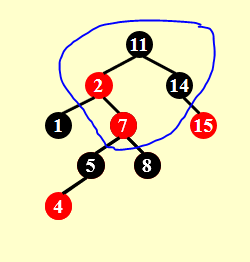
插入前:
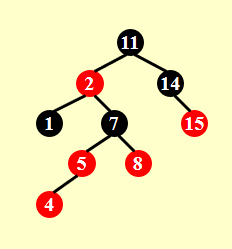
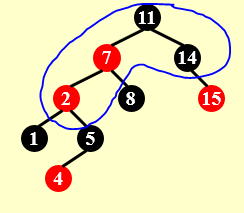
插入4:
变换颜色,但上一层不满足红黑树定义了:
旋转,变换为case2:
变色并旋转:
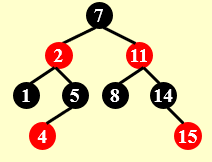
结束
待续