线代：1.5矩阵的秩(zhi)

本课程来自 深度之眼，部分截图来自课程视频。
【第一章 线性代数】1.5矩阵的秩
在线LaTeX公式编辑器

任务详解：

1、掌握矩阵的秩是如何计算的，以及秩和初等变换的关系，以及秩的性质
2、掌握线性方程组的情况

矩阵的秩Rank of matrix

定义3

在m×n矩阵A中，任取k行与k列（k≤m，k≤n），位于这些行列交叉处的 $k^2$个元素，不改变它们在A中所处的位置次序而得的k阶行列式，称为矩阵A的k阶子式.
m×n矩阵A的k阶子式共有 $C_m^k\cdot C_n^k$个.

定义4

设在矩阵A中有一个不等于0的r阶子式D，且所有r+1阶子式（如果存在的话）全等于0，那么D称为矩阵A的最高阶非零子式，数r称为矩阵A的秩，记作R(A).并规定零矩阵的秩等于0。
显然，若A为m×n矩阵，则0≤R(A).≤min{m,n}.
由于行列式与其转置行列式相等，因此 $A^T$的子式与A的子式对应相等，从而 $R(A^T)=R(A)$
对于n阶矩阵A，由于A的n阶子式只有一个lAl，故当lAl≠0时R(A)=n，当|A|=0时R(A)<n。可见可逆矩阵的秩等于矩阵的阶数，不可逆矩阵的秩小于矩阵的阶数。因此，可逆矩阵又称满秩矩阵，不可逆矩阵（奇异矩阵）又称降秩矩阵。

定理2（判断两个矩阵的秩的关系）

若A~B，则R(A)=R(B)
推论：若可逆矩阵P，Q使PAQ=B，则R(A)=R(B)
这个推论证明很简单，P，Q可逆，根据上一个小节的定理可以写为：
$P=p_1p_2...p_m,\quad Q=q_1q_2...q_n$
$PAQ=p_1p_2...p_mAq_1q_2...q_n=B$
等式左边相当于对A做了m次初等行变换，和n次初等列变换最后得到B，也就是A~ B，根据定理2R(A)=R(B)
例子：
求矩阵A及矩阵B=（A，b）的秩。（这里的B是增广矩阵，就相当于方程组中x的系数加上最后系数b组成的矩阵。）

因此，R（A）=2，R（B）=3.这里A的秩只看左边四列即可。
从矩阵B的行阶梯形矩阵可知，本例中的A与b所对应的线性方程组Ax=b是无解的，这是因为行阶梯形矩阵的第3行表示矛盾方程0=1.
这里其实隐含一个推论：R(A)<R(B)，也就是方程组系数的秩小于增广矩阵的秩，方程组无解。

秩的性质

1、 $0 \leqslant R(A_{m\times n})\leqslant min|m,n|$：一个矩阵的秩小于等于秩的维度
2、 $R(A^T)=R(A)$：矩阵和矩阵转置的秩相等
3、若A~B，则 $R(A)=R(B)$：两个矩阵等价，矩阵也相等
4、若P、Q可逆，则 $R(PAQ)=R(A)$：就是定理二的推论
5、 $max \left \{R(A),R(B) \right \}\leqslant R(A,B)\leqslant R(A)+R(B)$：A和B的秩的较大者，要比AB拼接起来的矩阵的秩要小。可以看成两个：
$R(A)\leqslant R(A,B)$、 $R(B)\leqslant R(A,B)$
当B=b为非零列向量时(非零列向量≤1)，有： $R(A)\leqslant R(A,b)\leqslant R(A)+1$
6、 $R(A+B)\leqslant R(A)+R(B)$
证明： $R(A+B)\leqslant R(A+B,B)=R(A,B)\leqslant R(A)+R(B)$
7、 $R(AB)\leqslant min \left \{R(A)+R(B)\right \}$，当A或B为单位矩阵的时候等号成立。
这个很重要，在后面推导多元线性回归的时候要用。
8、 $A_{m\times n}B{n\times l}=0$，则 $R(A)+R(B)\leqslant n$

线性方程组的解

设有n个未知数m个方程的线性方程组，表示为矩阵m是行数，n是列数。

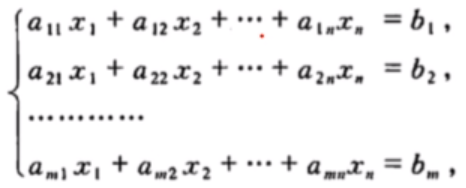
上式可以写成以向量x为未知元的向量方程： $Ax=b$

定理3

n元线性方程组Ax=b
（i）无解的充分必要条件是R(A)<R(A,b)；超静定方程，m＞n
（ii）有惟一解的充分必要条件是R(A)=R(A，b)=n；n为未知数的个数。
（iii）有无限多解的充分必要条件是R(A)=R(A,b)<n。静不定方程，m＜n
定理4：n元齐次线性方程组Ax=0有非零解的充分必要条件是R(A)<n，相当于b=0，此时： $R(A)=R(A,b)$，所以满足定理3中的第二或第三个条件，但是现在要非零解，因此，是满足第三个条件R(A)=R(A,b)<n，即R(A)<n。
定理5：线性方程组Ax=b有解的充分必要条件是R(A)=R(A,b)