2020-2-4 深度学习笔记6 - 深度前馈网络1（XOR实现）

第六章 深度前馈网络1（XOR实现）

官网

深度前馈网络，也叫作前馈神经网络或者多层感知机，是典型的深度学习模型。
前馈网络的目标是近似某个函数 $f^*$。 例如，对于分类器， $y = f^*(x)$将输入 $x$映射到一个类别 $y$。 前馈网络定义了一个映射 $y = f(x; \theta)$，并且学习参数 $\theta$的值，使它能够得到最佳的函数近似。

解释一下“深度前馈网络”

• 这种模型被称为前向（feedforward）的，是因为信息流过 $x$的函数，流经用于定义 $f$的中间计算过程，最终到达输出 $y$。 在模型的输出和模型本身之间没有反馈（feedback）连接。
  • 前馈网络应用
    • 用于对照片中的对象进行识别的卷积神经网络就是一种专门的前馈网络。
    • 当前馈神经网络被扩展成包含反馈连接时，它们被称为循环神经网络（recurrent neural network）。 前馈网络是通往循环网络之路的概念基石，后者在自然语言的许多应用中发挥着巨大作用。
• 前馈神经网络被称作网络是因为它们通常用许多不同函数复合在一起来表示。该模型与一个有向无环图相关联，而图描述了函数是如何复合在一起的。
  • 例如，有三个函数 $f^{(1)}, f^{(2)}$和 $f^{(3)}$连接在一个链上以形成 $f(x) = f^{(3)}(f^{(2)}(f^{(1)}(x)) )$。 这些链式结构是神经网络中最常用的结构。
  • 在这种情况下， $f^{(1)}$被称为网络的第一层， $f^{(2)}$被称为第二层，以此类推。
  • 链的全长称为模型的深度（depth）。 正是因为这个术语才出现了”深度学习”这个名字。

深度前馈网络的各层之间有什么区别呢？

1.前馈网络的最后一层被称为输出层（output layer）。

• 在神经网络训练的过程中，我们让 $f(x)$去匹配 $f^*(x)$的值。 训练数据为我们提供了在不同训练点上取值的、含有噪声的 $f^*(x)$的近似实例。
• 每个样本 $x$都伴随着一个标签 $y\approx f^*(x)$。 （有监督学习）
• 训练样本直接指明了输出层在每一点 $x$上必须做什么；它必须产生一个接近 $y$的值。

2.训练数据 并没有直接指明其他层应该怎么做。学习算法必须决定如何使用这些层来产生想要的输出，但是训练数据并没有说每个单独的层应该做什么。 相反，学习算法 必须决定如何使用这些层来最好地实现 $f^*$的近似。 因为训练数据并没有给出这些层中的每一层所需的输出，所以这些层被称为隐藏层（hidden layer）。

为什么这些网络之所以被称为神经网络？

因为或多或少地受到神经科学的启发。

• 网络中的每个隐藏层通常都是向量值的。这些隐藏层的维数决定了模型的宽度。 向量的每个元素都可以被视为起到类似一个神经元的作用。
• 除了将层想象成向量到向量的单个函数，我们也可以把层想象成由许多并行操作的单元组成，每个单元表示一个向量到标量的函数。 每个单元在某种意义上类似一个神经元，它接收的输入来源于许多其他的单元，并计算它自己的激活值。

一种理解前馈网络的方式是从线性模型开始，并考虑如何克服它的局限性。如果各层的函数f都是线性函数，那么复合后的函数依然是线性的，此时我们的网络模型等价于线性模型。为了提高模型的表示能力，我们需要将各层的f设置为非线性的，从而得到一个非线性映射φ我们可以认为φ(x)提供了一组描述x的特征，或者认为它提供了x的一个新的表示。

那么如何选择映射 $\phi$？

• 一种选择是使用一个通用的 $\phi$，例如无限维的 $\phi$，它隐含地用在基于RBF核的核机器上。但是非常通用的特征映射通常只基于局部光滑的原则，并且没有将足够的先验信息进行编码来解决高级问题。
• 另一种选择是手动地设计 $\phi$。 这种方法对于每个单独的任务都需要人们数十年的努力，从业者各自擅长特定的领域（如语音识别或计算机视觉），并且不同领域之间很难迁移(transfer)。
• 深度学习的策略是去学习 $\phi$。在这种方法中，我们有一个“深度前馈网络”模型 $y = f(x;\theta, w) = \phi(x; \theta)^T w$， $\phi$定义了一个隐藏层，包含2个参数
  • 从一大类函数中学习 $\phi$的参数θ
  • 用于将φ(x)映射到所需的输出的参数w
    我们将表示参数化为 $\phi(x; \theta)$，并且使用优化算法来寻找 $\theta$，使它能够得到一个好的表示【将原始数据转换为能够被机器学习有效开发的一种形式】。

第三种方法是三种方法中唯一一种放弃了训练问题的凸性的，但是利大于弊。
这种方法也可以通过使它变得高度通用以获得第一种方法的优点——我们只需使用一个非常广泛的函数族 $\phi(x; \theta)$。
这种方法也可以获得第二种方法的优点。 人类专家可以将他们的知识编码进网络来帮助泛化，他们只需要设计那些他们期望能够表现优异的函数族 $\phi(x; \theta)$即可。

学习XOR（异或）函数

参考链接1，链接2
本节学习利用前馈网络解决一个非常简单的任务：学习XOR函数。

XOR函数（”异或”逻辑）是两个二进制值 $x_1$和 $x_2$的运算。 当这些二进制值中恰好有一个为1时，XOR函数返回值为1。 其余情况下返回值为0。

训练一个前馈网络至少需要做和线性模型同样多的设计决策：选择一个优化模型、代价(损失)函数以及输出单元的形式。

XOR函数提供了我们想要学习的目标函数 $y = f^*(x)$。 我们的模型给出了一个函数 $y=f(x; \theta)$并且我们的学习算法会不断调整参数 $\theta$来使得 $f$尽可能接近 $f^*$。

我们希望网络在这四个点 $X =\{[0, 0]^T, [0, 1]^T, [1, 0]^T, [1, 1]^T\}$上表现正确。 我们会用全部这四个点来训练我们的网络，唯一的挑战是拟合训练集。

训练集的设计矩阵

x1	x2	y
0	0	0
0	1	1
1	0	1
1	1	0

我们可以把这个问题当作是回归问题，并使用均方误差损失函数。 我们选择这个损失函数是为了尽可能简化本例中用到的数学。

评估整个训练集上表现的MSE损失函数为
$J(θ)=\frac14 \sum_{x∈X}(f^∗(x)−f(x;θ))^2$
下一步要选择模型 $f(x; \theta)$的形式
假设我们选择一个线性模型， $\theta$包含 $w$和 $b$，那么我们的模型被定义成 $f(x;w,b)=x^⊤w+b$。
x,w为向量，b为标量

在神经网络中现在只有1层(这是一个神经元)：

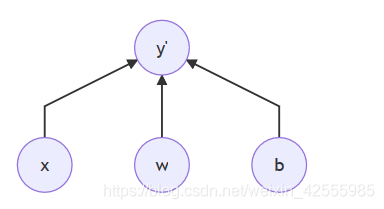
更简单一些的描述为(标记这种图时，通常省略截距项)，一个函数操作意味着一层(更概念化一些)：

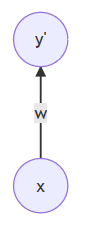
通常用这幅图来描述一层神经网络。X节点是Y节点的父节点。

我们可以使用正规方程关于 $w$和 $b$最小化 $J(\theta)$，来得到一个闭式解。

解正规方程以后，我们得到w＝0以及 $b=\frac 12$。线性模型仅仅是在任意一点都输出0.5，显然不能用来表示XOR函数。
观察下图（图1）
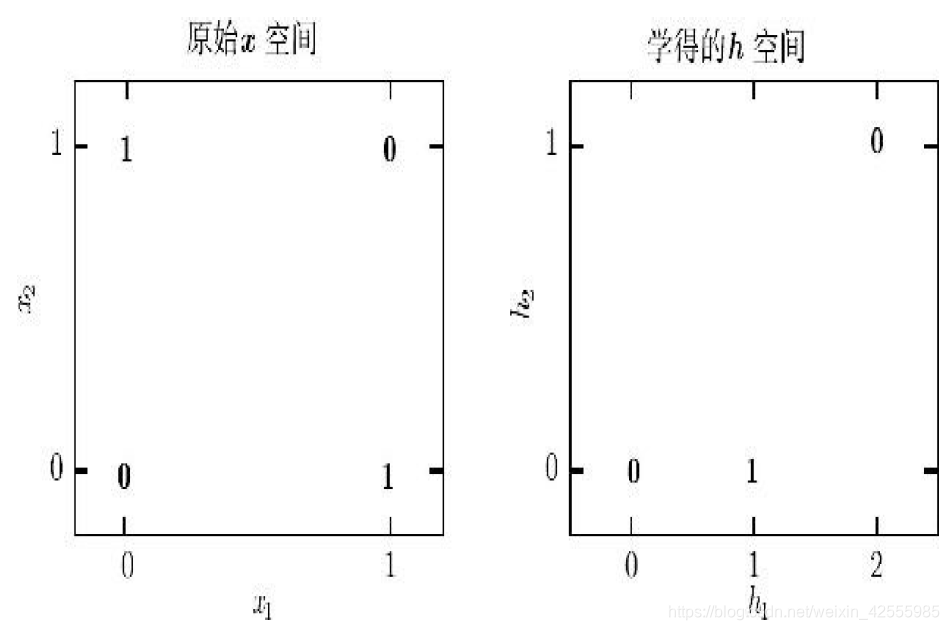图上的粗体数字标明了学得的函数必须在每个点输出的值。
左图直接应用于原始输入的线性模型不能实现XOR函数。

• 当 $x_1 = 0$时，模型的输出必须随着 $x_2$的增大而增大。
• 当 $x_1 = 1$时，模型的输出必须随着 $x_2$的增大而减小。

而线性模型必须对 $x_2$使用固定的系数 $w_2$。因此，线性模型不能使用 $x_1$的值来改变 $x_2$的系数，从而不能解决这个问题。

右图变换了特征空间。输出必须为1的两个点折叠到了特征空间中的单个点。
非线性特征将 $x = [1, 0]^T$和 $x = [0, 1]^T$都映射到了特征空间中的单个点 $h = [1, 0]^T$。线性模型现在可以将函数描述为 $h_1$增大和 $h_2$减小。
在这里我们引入一个非常简单的前馈神经网络，它有一层隐藏层，隐藏层中包含两个单元。
观察下图

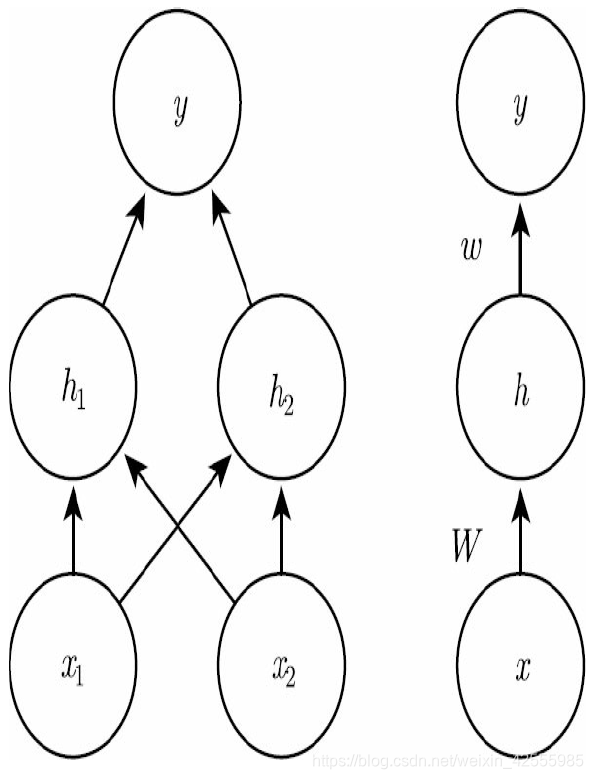
上图是使用两种不同样式绘制的前馈网络的示例
左图在这种样式中，我们将每个单元绘制为图中的一个节点。如果是更大的网络，它可能会消耗太多右图在这种样式中，我们将表示每一层激活的整个向量绘制为图中的一个节点。这种样式更加紧凑。
在右图中，我们对边使用参数名进行注释，这些参数是用来描述两层之间的关系的。这里，我们用矩阵描述从x到h的映射，用向量w描述从h到y的映射。当标记这种图时，我们通常省略与每个层相关联的截距参数。

回到前馈网络选择。
这个前馈网络有一个通过函数 $f^{(1)}(x;W, c)$计算得到的隐藏单元的向量 $h$。 这些隐藏单元的值随后被用作第二层的输入。 第二层就是这个网络的输出层。 输出层仍然只是一个线性回归模型，只不过现在它作用于h而不是x。
整个网络现在包含链接在一起的两个函数： $h=f^{(1)}(x; W, c)=W^Tx+c$和 $y = f^{(2)}(h; w, b)=w^Th+b$
完整的模型是 $f(x; W, c, w, b) = f^{(2)}(f^{(1)}(x))$。

那么 $f^{(1)}$应该是哪种函数？
线性模型到目前为止都表现不错，让 $f^{(1)}$也是线性的似乎很有诱惑力。可惜的是，因为作为输出层的 $f^{(2)}$已经是线性的，如果 $f^{(1)}$再是线性的，那么前馈网络作为一个整体对于输入仍然是线性的。
现在我们暂时忽略截距项c和b，假设 $h=f^{(1)}(x)= W^T x$并且 $f^{(2)}(h)=w^Th$，那么 $f(x) = w^T W^T x$。
我们可以将这个函数重新表示成 $f(x) = x^T w’$其中 $w’ = Ww$。

显然，我们必须用非线性函数来描述这些特征。
大多数神经网络通过仿射变换【一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间】之后紧跟着一个被称为激活函数【负责将神经元的输入映射到输出端。增加神经网络模型的非线性】的固定非线性函数来实现这个目标，其中仿射变换由学得的参数控制。
【补充-常用的激活函数】
1.sigmod函数， $f(x)=\frac1{1+e^{−1}}$
2.tanh函数， $f(x)=\frac{e^x−e^{−x}}{e^x+e^{−x}}$
3.Relu函数， $f(x)=\begin{cases}0,x≤0\\x,x>0\end{cases}$

我们这里使用这种策略，定义仿射变换 $h=g(W^T x+c)$，其中 $W$是线性变换的权重矩阵， $c$是偏置。

前面一层神经网络使用的线性回归模型 $f(x;w,b)=x^⊤w+b$，其中x,w为向量，b为标量。使用权重向量w和一个标量b的偏置参数来描述从 输入向量 到 输出标量 的仿射变换。

现在仿射变换 $h=g(W^T x+c)$，是向量 $x$到向量 $h$的仿射变换，所以我们需要一整个向量的偏置参数。

激活函数 $g$通常选择对每个元素分别起作用的函数，有 $h_i =g(x^TW_{:, i} + c_i)$。 在现代神经网络中，默认的推荐是使用由激活函数 $g(z)=\max\{0, z\}$定义的整流线性单元（rectified linear unit）或者称为ReLU。

上图是整流线性激活函数。
该激活函数是被推荐用于大多数前馈神经网络的默认激活函数。将此函数用于线性变换的输出将产生非线性变换。然而，函数仍然非常接近线性，在这种意义上它是具有两个线性部分的分段线性函数。

由于整流线性单元几乎是线性的，因此它们保留了许多使得线性模型易于使用基于梯度的方法进行优化的属性。它们还保留了许多使得线性模型能够泛化良好的属性。

计算机科学的一个公共原则是，我们可以从最小的组件构建复杂的系统。就像图灵机的内存只需要能够存储0或1的状态，我们可以从整流线性函数构建一个万能函数近似器

现在总结一下，由 $h=g(W^T x+c)$，激活函数 $g(z)=\max\{0, z\}$，得到 $h=\max(0,W^T x+c)$
再由 $y = f^{(2)}(h; w, b)=w^Th+b$，得到整个网络函数为 $f(x; W, c, w, b)=w^T\max(0,W^T x+c)+b$

++++++++++++++++++++++++++++++++++++++++++++++++++++++++
【补充–神经元结构】
一般地，一个神经元的结构如下图所示。

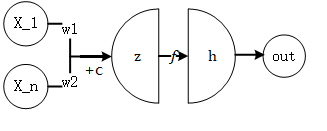
• x是训练数据集的样例
• W和c 是参数，常放在一起组成参数的集合θ
• z=W^T x+c是线性函数输出量
• h=f(z)，其中f是激活函数
• out=h是输出量

这样的每一个单元叫做一个神经元。
每一层中单元的个数为神经网络的宽度。h的维度就是该层神经网络中的神经元个数，也是该层的宽度。

+++++++++++++++++++++++++++++++++++++++++++++++++++++++

我们现在可以给出XOR问题的一个解。
现在神经网络的两个输入均有两个取值0和1，那么组合起来就有四种可能，即[0，0]、[0，1]、[1，0]、[1，1]，这样就可以通过中间的隐藏层进行异或。
具体实现代码说明参见链接。只有一点小小区别：链接中输入层到隐藏层的权重参数是一个w1，本例中用了2个w1_1和w1_2。偏移量也是一样的。
令
$W=\begin{bmatrix} 1 & 1 \\ 1 & 1 \\ \end{bmatrix}$ $c=\begin{bmatrix}0&-1\end{bmatrix}$ $w=\begin{bmatrix} 1 \\ -2 \end{bmatrix}$以及b=0

令 $X$表示输入矩阵。它包含二进制输入空间中全部的四个点，每个样本占一行，那么输入矩阵表示为： $X=\begin{bmatrix} 0 & 0 \\ 0 & 1 \\ 1 & 0 \\ 1 & 1 \\ \end{bmatrix}$

开始计算
神经网络的第一步是将输入矩阵乘以第一层的权重矩阵： $XW=\begin{bmatrix} 0 & 0 \\ 1 & 1 \\ 1 & 1 \\ 2 & 2 \\ \end{bmatrix}$
然后，我们加上偏置向量 $c$，得到 $XW+c=\begin{bmatrix} 0 & -1 \\ 1 & 0 \\ 1 & 0 \\ 2 & 1 \\ \end{bmatrix}$
在这个空间中，所有的样本都处在一条斜率为1的直线上（y=x-1）。 当我们沿着这条直线移动时，输出需要从0升到1，然后再降回0。 线性模型不能实现这样一种函数。
为了用 $h$对每个样本求值（ $h=g(W^Tx+c)$），我们使用整流线性变换 $g(z)=\max\{0, z\}$： $\begin{bmatrix} 0 & 0 \\ 1 & 0 \\ 1 & 0 \\ 2 & 1 \\ \end{bmatrix}$
这个变换改变了样本间的关系。它们不再处于同一条直线上了。 如《图1》所示，它们现在处在一个可以用线性模型解决的空间上。
我们最后乘以一个权重向量 $w$:
$\begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \\ \end{bmatrix}$
神经网络对这一批次中的每个样本都给出了正确的结果。

代码实现

import tensorflow as tf
import numpy as np
#定义输入值（训练数据）与目标值（标签）
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([[0], [1], [1], [0]])

#定义占位符，从输入或目标中按行取数据
x = tf.placeholder(tf.float32, [None, 2])
y = tf.placeholder(tf.float32, [None, 1])

#初始化权重，使其满足正态分布，w1_1和w1_2分别为输入层到隐藏层的权重矩阵
#w2为隐藏层到输出层的权重矩阵
w1_1 = tf.Variable(tf.random_normal([2, 1]))
w1_2 = tf.Variable(tf.random_normal([2, 1]))
w2 = tf.Variable(tf.random_normal([2, 1]))

#定义偏移量，分别为隐藏层（b1_1和b1_2）和输出层的偏移量b2
b1_1 = tf.constant(0.1, shape=[1])
b1_2 = tf.constant(0.1, shape=[1])
b2 = tf.constant(0.1, shape=[1])

#使用Relu激活函数得到隐藏层的输出值
#隐藏层神经元功能就是将输入值和相应权重做矩阵乘法，然后加上偏移量，最后使用激活函数进行非线性转换
h1 = tf.nn.relu(tf.matmul(x, w1_1) + b1_1)
h2 = tf.nn.relu(tf.matmul(x, w1_2) + b1_2)

# 将两数组按列合并
hidden = tf.concat([h1, h2], 1)  
out = tf.matmul(hidden, w2) + b2 #输出层不用激活函数，直接获得其值

#定义损失（代价）函数MSE
loss = tf.reduce_mean(tf.square(out - y))

#优化器选择Adam
train = tf.train.AdamOptimizer(0.01).minimize(loss) #学习率0.01

#开始训练，迭代1000次
#每次迭代过程都将使用训练集的新数据修改节点的权重。
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())#初始化变量
    for i in range(1000):
        for j in range(4):
            sess.run(train, feed_dict={x: np.expand_dims(X[j], 0), y: np.expand_dims(Y[j], 0)})#训练模型
        loss_ = sess.run(loss, feed_dict={x: X, y: Y})#获取损失
        print("step: %d, loss: %.3f"%(i, loss_)) # 输出训练误差
    print("X: %r"%X) #输出测试数据
    print("pred: %r"%sess.run(out, feed_dict={x: X}))  #输出测试数据预测的结果

执行结果

(tensorflow) C:\Users\toddc>python C:\todd\python_files\DeepLearning\test.py
C:\Users\toddc\Anaconda3\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:469: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
  _np_qint8 = np.dtype([("qint8", np.int8, 1)])
C:\Users\toddc\Anaconda3\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:470: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
  _np_quint8 = np.dtype([("quint8", np.uint8, 1)])
C:\Users\toddc\Anaconda3\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:471: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
  _np_qint16 = np.dtype([("qint16", np.int16, 1)])
C:\Users\toddc\Anaconda3\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:472: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
  _np_quint16 = np.dtype([("quint16", np.uint16, 1)])
C:\Users\toddc\Anaconda3\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:473: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
  _np_qint32 = np.dtype([("qint32", np.int32, 1)])
C:\Users\toddc\Anaconda3\envs\tensorflow\lib\site-packages\tensorflow\python\framework\dtypes.py:476: FutureWarning: Passing (type, 1) or '1type' as a synonym of type is deprecated; in a future version of numpy, it will be understood as (type, (1,)) / '(1,)type'.
  np_resource = np.dtype([("resource", np.ubyte, 1)])
2020-02-05 14:50:10.139637: I C:\tf_jenkins\home\workspace\rel-win\M\windows\PY\36\tensorflow\core\platform\cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: AVX AVX2
step: 0, loss: 0.279
step: 1, loss: 0.275
step: 2, loss: 0.270
step: 3, loss: 0.266
step: 4, loss: 0.263
step: 5, loss: 0.260
step: 6, loss: 0.258
step: 7, loss: 0.256
step: 8, loss: 0.253
step: 9, loss: 0.251
step: 10, loss: 0.249
step: 11, loss: 0.247
step: 12, loss: 0.245
step: 13, loss: 0.243
step: 14, loss: 0.241
step: 15, loss: 0.238
step: 16, loss: 0.236
step: 17, loss: 0.233
step: 18, loss: 0.231
step: 19, loss: 0.228
step: 20, loss: 0.225
step: 21, loss: 0.222
step: 22, loss: 0.219
step: 23, loss: 0.216
step: 24, loss: 0.213
step: 25, loss: 0.209
step: 26, loss: 0.206
step: 27, loss: 0.202
step: 28, loss: 0.198
step: 29, loss: 0.194
step: 30, loss: 0.190
step: 31, loss: 0.186
省略
step: 988, loss: 0.012
step: 989, loss: 0.012
step: 990, loss: 0.012
step: 991, loss: 0.011
step: 992, loss: 0.011
step: 993, loss: 0.011
step: 994, loss: 0.011
step: 995, loss: 0.011
step: 996, loss: 0.011
step: 997, loss: 0.011
step: 998, loss: 0.011
step: 999, loss: 0.011
X: array([[0, 0],
       [0, 1],
       [1, 0],
       [1, 1]])
pred: array([[0.18906632],
       [0.9909844 ],
       [0.99562013],
       [0.1       ]], dtype=float32)

最后损失降为0.011了。观察一下我们的预测值，四项分别对应[0,1,1,0]，已经是相当接近了
神经网络中的超参中最重要的就是学习率了，如果损失一直降不下来，我们首先要想到修改学习率，其他的超参次之。本例中学习率是0.01，如果改为0.1，那损失就会很大。即使再增加训练次数，损失也不会下降。

学习率：决定参数移动到最优值的速度快慢。学习率过大，会越过最优值。学习率过小，优化效率低。

关于tensorflow语法说明

• x = tf.placeholder(tf.float32, [None, 2])
  tensorflow中在运行时动态设置某个变量的值，先使用placeholder占位（我猜测是开辟内存吧）。运行时动态给占位符“喂”数据。

tf.placeholder(dtype,shape=None,name=None)
 -  dtype：数据类型。常用的是tf.float32,tf.float64等数值类型
 -  shape：数据形状。默认是None，就是一维值，也可以是多维（比如[2,3], [None, 3]表示列是3，行不定）
 -  name：名称

• w1_1 = tf.Variable(tf.random_normal([2, 1]))
  tf.Variable()创建变量
  tf.random_normal用于从服从指定正太分布的数值中取出指定个数的值。

tf.random_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None)
 - shape: 输出张量(Tensor)的形状，必选
 - mean: 正态分布的均值，默认为0
 - stddev: 正态分布的标准差，默认为1.0
 - dtype: 输出的类型，默认为tf.float32
 - seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样
 - name: 操作的名称

• b1_1 = tf.constant(0.1, shape=[1])
  tf.constant创建常量

tf.constant(    value,    dtype=None,    shape=None,    name='Const',    verify_shape=False)
 - value，必须，常量数值或者 list，输出张量的值
 - dtype，输出张量元素类型
 - shape，输出张量的维度
 - name，张量名称
 - verify_shape，检测 shape 是否和 value 的 shape 一致，若为 Fasle，不一致时，会用最后一个元素将 shape 补全

• h1 = tf.nn.relu(tf.matmul(x, w1_1) + b1_1)，定义模型。relu：整流线性单元。
  tf.nn.relu，计算激活函数，即 max(features, 0)。将大于0的保持不变，小于0的数置为0。就是那个 $g(z)=\max\{0, z\}$。

tf.nn.relu(features, name = None)

tf.matmul，将矩阵a乘以矩阵b，生成a * b。

tf.matmul(a, b, transpose_a=False, transpose_b=False, adjoint_a=False, adjoint_b=False, a_is_sparse=False, b_is_sparse=False, name=None) 

 - a: 一个类型为 float16, float32, float64, int32, complex64, complex128 且张量秩 > 1 的张量。 
 - b: 一个类型跟张量a相同的张量。
 - transpose_a: 如果为真, a则在进行乘法计算前进行转置。
 - transpose_b: 如果为真, b则在进行乘法计算前进行转置。 
 - adjoint_a: 如果为真, a则在进行乘法计算前进行共轭和转置。
 - adjoint_b: 如果为真, b则在进行乘法计算前进行共轭和转置。 
 - a_is_sparse: 如果为真, a会被处理为稀疏矩阵。 
 - b_is_sparse: 如果为真, b会被处理为稀疏矩阵。 
 - name: 操作的名字（可选参数） 
返回值： 一个跟张量a和张量b类型一样的张量且最内部矩阵是a和b中的相应矩阵的乘积。

• hidden = tf.concat([h1, h2], 1)
  tf.concat拼接张量

tf.concat([tensor1, tensor2, tensor3,...], axis)

axis=0，代表在第0个维度拼接；axis=1，代表在第1个维度拼接
对于一个二维矩阵，第0个维度代表最外层方括号所框下的子集，第1个维度代表内部方括号所框下的子集。维度越高，括号越小。
例：

  t1 = [[1, 2, 3], [4, 5, 6]]
  t2 = [[7, 8, 9], [10, 11, 12]]
  tf.concat([t1, t2], 0)  # [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
  tf.concat([t1, t2], 1)  # [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]]

• tf.square(out - y)
  tf.square(a)，对a中的每一个元素求平方
• tf.reduce_mean(tf.square(out - y))
  tf.reduce_mean()，计算张量tensor沿着指定的数轴（tensor的某一维度）上的的平均值。主要用作降维或者计算tensor的平均值。

reduce_mean(input_tensor,  axis=None,  keep_dims=False,   name=None,  reduction_indices=None)
第一个参数 input_tensor： 输入的待降维的tensor;
第二个参数 axis： 指定的轴，如果不指定，则计算所有元素的均值;
第三个参数 keep_dims：是否降维度，设置为True，输出的结果保持输入tensor的形状，设置为False，输出结果会降低维度;
第四个参数 name： 操作的名称;
第五个参数 reduction_indices：在以前版本中用来指定轴，已弃用

loss = tf.reduce_mean(tf.square(logits-labels))，均方差函数是tf中常见的损失函数。
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
补充：均方差函数

均方差函数主要用于评估回归模型的使用效果，其概念相对简单，就是真实值与预测值差值的平方的均值，具体运算公式可以表达如下：

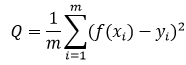
其中f(x_i)是预测值，y_i是真实值。在二维图像中，该函数代表每个散点到拟合曲线y轴距离的总和，非常直观。
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

• train = tf.train.AdamOptimizer(0.01).minimize(loss)
  AdamOptimizer，tensorflow内置优化算法。此函数是Adam优化算法：是一个寻找全局最优点的优化算法，引入了二次方梯度校正。

class tf.train.AdamOptimizer
__init__(learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08, use_locking=False, name='Adam')
Args:

 -  learning_rate: A Tensor or a floating point value. The learning rate.
 -  beta1: A float value or a constant float tensor. The exponential decay rate for the 1st moment estimates.
 -  beta2: A float value or a constant float tensor. The exponential decay rate for the 2nd moment estimates.
 -  epsilon: A small constant for numerical stability. This epsilon is "epsilon hat" in the Kingma and Ba paper (in the formula just before Section 2.1), not the epsilon in Algorithm 1 of the paper.
 -  use_locking: If True use locks for update operations.
 -  name: Optional name for the operations created when applying gradients. Defaults to "Adam".

• sess.run(tf.global_variables_initializer())，初始化模型的参数。变量运行前必须做初始化操作。

 -  lobal_variables_initializer 返回一个用来初始化 计算图中 所有global variable的 op。
 	-   TensorFlow 是一个编程系统, 使用图来表示计算任务.图中的节点被称之为 op (operation 的缩写). 一个 op 获得 0 个或多个Tensor, 执行计算, 产生 0 个或多个 Tensor. 每个 Tensor 是一个类型化的多维数组. 例如, 你可以将一小组图像集表示为一个四维浮点数数组, 这四个维度分别是 [batch, height, width, channels].
 	-   函数中调用了 variable_initializer() 和 global_variables() 
 -  global_variables() 返回一个 Variable list ，里面保存的是 gloabal variables。
 -  variable_initializer() 将 Variable list 中的所有 Variable 取出来，将其 variable.initializer 属性做成一个 op group。
 -  然后看 Variable 类的源码可以发现， variable.initializer 就是一个 assign op。

所以，sess.run(tf.global_variables_initializer()) 就是 run了 所有global Variable 的 assign op，这就是初始化参数的本来目的。

• sess.run(train, feed_dict={x: np.expand_dims(X[j], 0), y: np.expand_dims(Y[j], 0)})
  feed_dict，给使用placeholder创建出来的tensor赋值。
  np.expand_dims:用于扩展数组的维度。

X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([[0], [1], [1], [0]])
print(X.shape) #(4, 2)
print(Y.shape) #(4, 1)
print(X[1])#[0 1]
c=np.expand_dims(X[1], 0)
print(c.shape) #(1, 2)
print(c)#[[0 1]]

++++++++++++++++++++++++++++++++++++++++++++++++++++++
【补充】
np.expand_dims(array, axis)指定位置插入新的轴来扩展数组形状。扩展维度

假设有一个数组A，数组A是一个两行三列的矩阵。大小我们记成（2,3）。
它的第“0”维，就是这个“2”行；第“1”维，就是这个“3”列。
expand_dims的作用，就是在第“axis”维，加一个维度出来，原先的“维”，推到右边去。
axis=0，那A矩阵的大小就变成了（1,2,3），就从2x3的二维矩阵变成了一个1x2x3的三维矩阵。
axis=1，矩阵大小就变成了（2,1,3），变成了一个2x1x3的三维矩阵。
axis=2，就变成（2,3,1)啦。

假设现在矩阵是2x3的矩阵，六个数字
1 2 3
4 5 6
axis=0，从2x3的二维矩阵变成了一个1x2x3的三维矩阵。
我们假设原来是一个二维平面，横坐标为x，纵坐标为y, 2x3的矩阵在这个XOY平面上。此时就是一个二维矩阵，（根本就没有z轴）
变换以后，现在变成了三维矩阵，变成了一个空间直角坐标系，有x，y，z三个轴。
原先的2x3的矩阵从XOY平面移动到了YOZ平面
（我们把原先的矩阵当成一个平摊在桌面上的纸片，变换以后，相当于给它立起来了），然后原先的X轴的“厚度”为1，此时虽然形式还是原来的数字，但是多了一个轴。

原先A[0][0]=1,A[0][1]=2,A[0][2]=3,A[1][0]=4……
axis=0，这时候矩阵从XOY平面移动到了YOZ平面，X轴只有一个值
那么,变换后的矩阵A’的第一个维度，只有一个值，就只能是0
A’[0][0][0]=1，A’[0][0][1]=2，A’[0][0][2]=3
A’[0][1][0]=4，A’[0][1][1]=5，A’[0][1][2]=6
A’[0][0]不指定第三维，就是[1,2,3]
A’[0][1]不指定第三维，就是[4,5,6]
那A’[1][0][0]……呢？不好意思，没有，因为第一维只能取一个数，就是0。

axis=1，就是从XOY面的矩阵，给它立起来到XOZ平面，在Y轴的厚度为1。
axis=2，就是从XOY面的矩阵，还是放在XOY面上。但是这时候多了一个z轴，（相当于这个操作之后可以在桌面的纸片上面，叠加新的纸片了）
++++++++++++++++++++++++++++++++++++++++++++++++++++++