【AI绘图学习笔记】深度前馈网络(三)

有关深度前馈网络的部分知识，我们已经在吴恩达的机器学习课程中有过了解了，本章主要是对《深度学习》花书中第六章：深度前馈网络的总结笔记。我希望你在看到这一章的时候，能回忆起机器学习课程中的一些环节或者细节，这对理解本文很有帮助。

参考笔记：
前馈神经网络初探——深度学习花书第六章（一）
神经网络损失函数、输出层、隐藏层详解——深度学习第六章（二）
反向传播算法——深度学习第六章（三）

---

---

反向传播和其他微分算法

当我们使用前馈神经网络接受输入$x$ 并产生输出$\hat{y}$时，信息通过网络前向流动，从输入层最终流动到输出层，我们将这样的传播过程称为前向传播 ，在训练过程中，前向传播从输入到隐藏层再到输出的正向流动过程，最终会产生一个标量代价函数$J(\theta )$。那么相反地，我们也可以允许来自代价函数的信息通过网络向后流动以便计算梯度，这个过程被我们称为反向传播。

要注意，有个普遍的误解是反向传播就是神经网络的全部学习算法，实际上，反向传播仅指计算梯度的过程，实际上的学习过程是诸如随机梯度下降(stochastic gradient descent，SGD) 更新网络的算法。

反向传播的原理很简单，就是利用了导数的链式法则:

$对于y=g(x),z=f(g(x))=f(y)，有\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}$

推广到矢量形式即为
${▽}_{x}z=(\frac{\partial y}{\partial x}{)}^T{▽}_{y}z({▽}_{x}z代表z对x求导的梯度)$

我们利用链式法则，就可以不断的从最终的损失函数不断的反向推导出每层的梯度，而反向传播就是一种特殊的进行链式法则运算的执行过程，即结合了动态规划(dynammic programming)避免了某些操作的重复性运算，利用较小的存储代价换取速度的提升。

链式法则实现反向传播

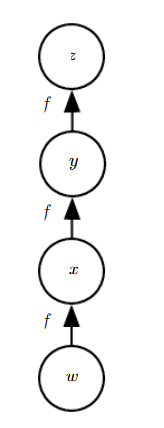
假设一个神经网络架构如下:

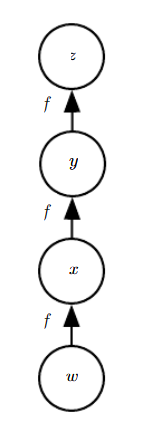
那么根据链式法则，我们想要计算z对w的梯度，则有:
$$\begin{gathered} \frac{\partial z}{\partial w} \\ =\frac{\partial z}{\partial y}\frac{\partial y}{\partial x}\frac{\partial x}{\partial w} \\ =f^{\prime }(y)f^{\prime }(x)f^{\prime }(w) \\ =f^{\prime }(f(f(w)))f^{\prime }(f(w))f^{\prime }(w) \end{gathered}$$

最终函数形式只剩下$f(w)$和其n阶导函数形式，好处在于减少了存储和运行时间

为了用简洁的符号来表示该算法，我们用计算图(computational graph) 来表示我们的神经网络，每个节点代表输入节点、隐藏层节点或输出节点，而每条边代表节点间的运算，例如对于 H = m a x { 0 , W X + b } H=max\{ {0,WX+b}\} H=max{ 0,WX+b},这样的一个ReLU函数可以由下图表示：

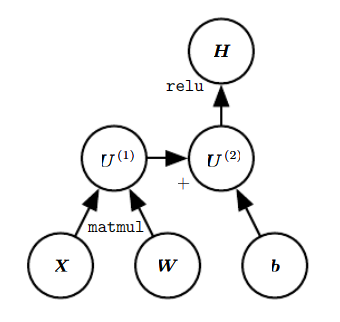
（在上图这个计算图中，被输入节点相当于一个计算操作，例如$U^{(1)}$对应矩阵乘法,$U^{(2)}$对应加法)

正向传播算法

假设我们计算$n_i$个输入节点用$u^{(1)}$至$u^{(n_i)}$映射到最终的损失输出$u^{(n)}$，则反向传播的目的是求出对于 i ∈ { 1 , 2.... n i } i \in \{ {1,2....n_i}\} i∈{ 1,2....ni​}的所有梯度。假设每一个中间的节点和其之前层的所有父节点的关系为$u^{(i)}=f^{(i)}({\mathbb{A}}^{(i)})$，其中${\mathbb{A}}^{(i)}=Pa(u^{(i)})$代表了$u^{(i)}$的所有父节点的集合，
其中每个节点通过将函数$f^{(i)}$应用到变量集合${\mathbb{A}}^{(i)}$上来计算$u^{(i)}$的值，${\mathbb{A}}^{(i)}$包含先前节点$u^{(j)}$的值满足$j<i$且$j\in Pa(u^{(i)})={\mathbb{A}}^{(i)}$，计算图的输入是向量$x$，并且被分配给前$n_i$个节点$u^{(1)}到u^{(n_i)}$，计算图的输出可以从最后一个(输出j)节点$u^{(n)}$读出。则正向传播算法可以表示为:

---

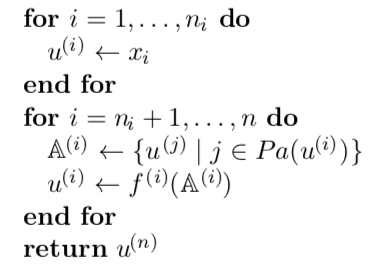
反向传播算法

对于反向传播过程，根据链式法则有:
$\frac{\partial u^{(n)}}{\partial u^{(j)}}={\sum }_{i:j\in Pa(u^{(i)})}\frac{\partial u^{(n)}}{\partial u^{(i)}}\frac{\partial u^{(i)}}{\partial u^{(j)}}$
即对于节点$u^{(j)}$（j属于i的所有父节点)，其导数等于所有其子节点$i$相对于$u^{(j)}$的导数与$u^{(n)}$相对于子节点导数的积的求和。

所以在经历过正向传播过程后，我们已经得到每个节点的值，反向传播计算梯度的算法则为

上面算法中的梯度表在一定程度上也体现了动态规划算法的思想。例如下图中的例子：

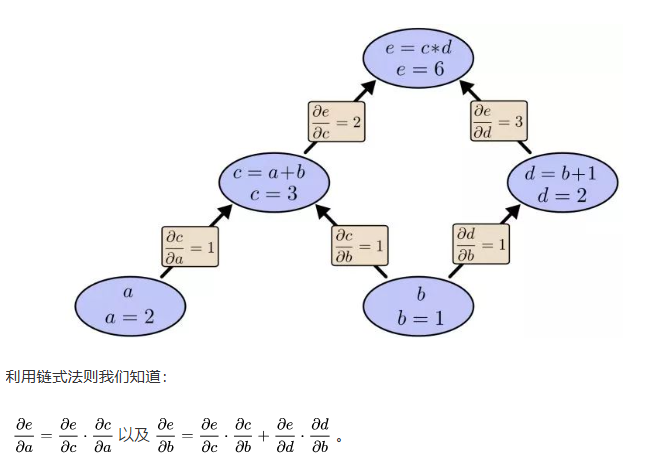
可以看出，反向传播算法中我们对于图中的每一条边只进行一次访问，减小了计算量。例如对于如下的计算图：

$$\begin{gathered} \frac{\partial z}{\partial w} \\ =\frac{\partial z}{\partial y}\frac{\partial y}{\partial x}\frac{\partial x}{\partial w}(反向传播) \\ =f^{\prime }(y)f^{\prime }(x)f^{\prime }(w) \\ =f^{\prime }(f(f(w)))f^{\prime }(f(w))f^{\prime }(w)(正向传播) \end{gathered}$$

如果不利用反向传播，为了得到$\frac{\partial zy}{\partial w}$则我们需要总共进行六次运算，而利用反向传播则仅进行三次运算即可。

总结一下，在正向传播过程中，我们计算了网络中每个节点的值，反向传播过程中利用这些值以及导数的链式法则结合动态规划的方法避免了重复运算，极大的提高了梯度计算速度，从而更加有利于利用梯度进行随机梯度下降更新神经网络参数完成机器学习训练任务。

---

全连接MLP中的反向传播计算

让我们考虑一个与全连接的多层MLP相关联的特定图，下面这个算法给出了对应的前向传播，它将参数映射到与单个训练样本（输入，目标）(x,y)相关联的监督损失函数$L(\hat{y},y)$，其中$\hat{y}$是当$x$提供输入时神经网络的输出。

这是典型深度神经网络的前向传播和代价函数的计算，损失函数$L(\hat{y},y)$取决于输出$\hat{y}$和目标$y$ 。为了获得总代价$J$，损失函数可以加上正则项$\Omega (\theta )$，其中$\theta$包含所有参数(权重矩阵和偏置参数)。该演示仅使用单个输入样本$x$，实际应用应该使用小批量。

在代数表达式和计算图中，我们都对符号(symbol) 或不具有特定值的变量进行操作，这些代数或者基于图的表达式被称为符号表示(symbolic representation)。当实际使用或训练神经网络的时候，我们必须要给这些符号赋值。

上述神经网络的反向计算，不止使用了输入$x$和目标$y$。该计算对于每一层$k$都产生了对激活变量$a^{(k)}$的梯度，从输出层开始向后计算直到到达第一个隐藏层。这些梯度可以看作对每层的输出应如何调整以减小误差的指导，根据这些梯度可以获得对每层参数的梯度。权重和偏置上的梯度可以立即用作随机梯度更新的一部分（梯度算出后即可执行更新），或者与其他基于梯度的优化算法一起使用。

一些反向传播的算法采用计算图和一组用于图的输入的数值，然后返回输出值处梯度的一组数值，这种先确定符号再计算数值的方法被称为符号到数值的微分。

如果我们仅仅使用计算图，可以添加一些额外的节点到图中，这些额外的节点提供了我们所需导数的符号描述，我们称其为符号到符号的方法。

符号到数值的方法可以理解为符号到符号图中完全相同的计算，关键区别在于符号到数值的方法不会显示出右侧的计算图。

（一般化的反向传播的正式算法内容略，本质上就是对我们总结的反向传播计算过程的伪代码实现，记录了一个关于梯度的雅可比矩阵gard_table进行计算）

用于MLP的反向传播的实例

现在我们给出一个网络隐藏层 H = m a x { 0 , X W ( 1 ) } H=max\{ {0,XW^{(1)}}\} H=max{ 0,XW(1)} ,此处为了简化不使用偏置参数$b$，现在给出代价函数:

$J=J_{MLE}+\lambda (\sum _{i,j}(W_{i,j}^{(1)}{)}^2+\sum _{i,j}(W_{i,j}^{(2)}{)}^2)$

它的计算图如下所示，进行计算后的新节点会用新的符号来表示：

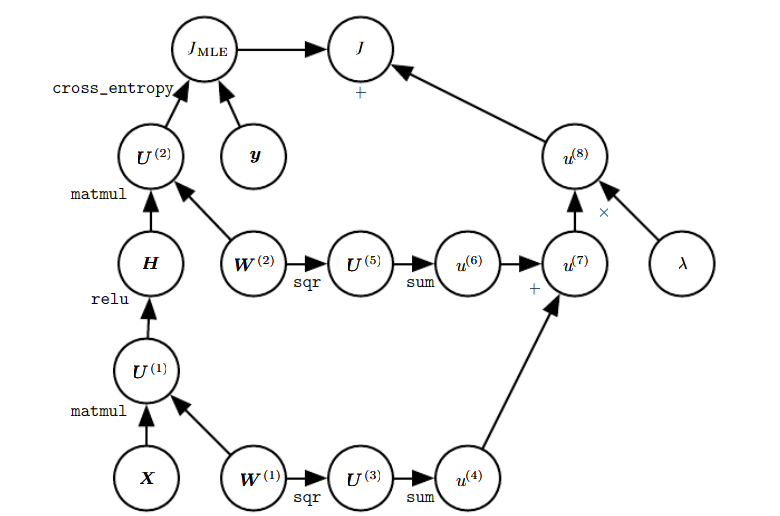
如果想要手动推导梯度是很麻烦的一件事，好在我们有反向传播算法可以自动生成梯度。我们可以通过观察上面这个正向传播图来描述反向传播算法的行为：

为了训练，我们希望计算出${▽}_{w^{(1)}}J$和${▽}_{w^{(2)}}J$，结合图像我们可知它代表了两种不同的路径从$J$后退到权重：一条通过交叉熵代价（左边），另一条通过权重衰减代价（右边）。权重衰减代价相对简单，它总是对$W^{(i)}$上的梯度贡献$2\lambda W^{(i)}(\lambda (W^{(i)}{)}^2求导)$

另一条交叉熵代价的路径就稍微复杂了，令$G$为未归一化对数概率$U^{(2)}$的梯度，接下来又分为了两个分支，右边的较短分支上，可以使用对矩阵乘法的第二个变量的反向传播规则，将$H^{T}G$加到$W^{(2)}$的梯度上。

另一条更长些的路径沿着网络逐步下降。首先，反向传播算法使用矩阵乘法的第一个变量的反向传播规则，计算${▽}_{H}J=G{W}^{(2)T}$，接下来ReLU操作使用其反向传播规则来对关于$U^{(1)}$的梯度中小于0的部分清零。记上述结果为$G^{\prime }$。反向传播的最后一步是使用对matmul操作的第二个变量的反向传播，将$X^T{G}^{\prime }$加到$W^{(1)}$的梯度上。

在计算了这些梯度以后，梯度下降算法或者其他优化算法要做的就是使用这些梯度更新参数。对于MLP而言，计算成本主要来源于矩阵乘法。