网络流基本概念
什么是网络流:
在一个有向图上选择一个源点,一个汇点,每一条边上都有一个流量上限(以下称为容量),即经过这条边的流量不能超过这个上界,同时,除源点和汇点外,所有点的入流和出流都相等,而源点只有流出的流,汇点只有汇入的流。这样的图叫做网络流。
所谓网络或容量网络指的是一个连通的赋权有向图 D= (V、E、C) , 其中V 是该图的顶点集,E是有向边(即弧)集,C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流,这是定义在网络上的非负函数,它一方面受到容量的限制,另一方面除去起点和终点以外,在所有中途点要求保持流入量和流出量是平衡的。
以上定义引自百度百科,本小白也看不懂,个人理解就是把网络图比作一个自来水管线网络,网络中的水管有粗有细(即流量限制),水从源点流入,最多能有多少水从汇点流出
我们定义:
源点:只有流出去的点
汇点:只有流进来的点
流量:一条边上流过的流量
容量:一条边上可供流过的最大流量
残量:一条边上的容量 - 流量
网络流最大流的求解:
网络流的所有算法都是基于一种增广路的思想,下面首先简要的说一下增广路思想,其基本步骤如下:
1.找到一条从源点到汇点的路径,使得路径上任意一条边的残量>0(注意是小于而不是小于等于,这意味着这条边还可以分配流量),这条路径便称为增广路
2.找到这条路径上最小的F[u][v](我们设F[u][v]表示u->v这条边上的残量即剩余流量),下面记为flow。(最小割定理,通俗的讲就一条管线的最大流量由口径最小的一段决定)
3.将这条路径上的每一条有向边u->v的残量减去flow,同时对于起反向边v->u的残量加上flow(为什么呢?我们下面再讲)
4.重复上述过程,直到找不出增广路,此时我们就找到了最大流
反向边
我们在寻找增广路的时候,在前面找出的不一定是最优解,如果我们在减去残量网络中正向边的同时将相对应的反向边加上对应的值,我们就相当于可以反悔从这条边流过。
举个例子:
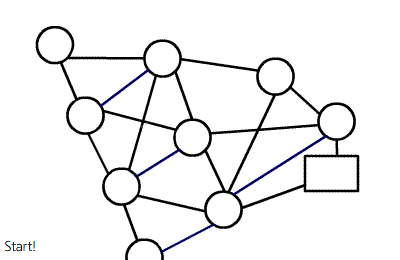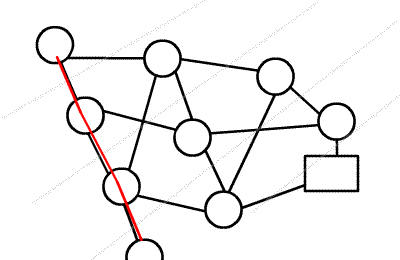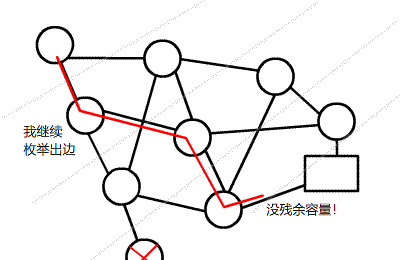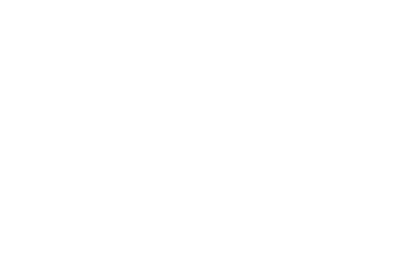
该图的源点是1,汇点是4,求最大流,显而易见该图的最大流是2。路径为1 -> 2 -> 4、1 -> 3 -> 4,两条路径的流量都是1。
但如果我们第一次找到的是 1 -> 2 -> 3 -> 4 这条增广路,这条路上的流量是1。于是我们修改后得到了下面这个流
这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前网络的流量是1。
嗯。。。 这个答案明显不对,因为我们可以同时走 1 -> 2 -> 4和 1 -> 3 -> 4,这样可以得到流量为2的流。
显然要给程序一个”后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。
于是我们就利用了一个叫做反向边的东西来解决这个问题。即每条边(i,j)都有一条反向边(j,i),反向边也同样有它的容量。
在第一次找到增广路之后,在把路上每一段的容量减少flow的同时,也把每一段上的反方向的容量增加flow。
这么做为什么会是对的呢?
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给”退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
这就是这个算法的精华部分,利用反向边,使程序有了一个后悔和改正的机会
Edmonds-Karp算法
原理
求最大流的过程,就是不断找到一条源到汇的路径,若有,找出增广路径上每一段[容量-流量]的最小值flow,然后构建残余网络,再在残余网络上寻找新的路径,使总流量增加。然后形成新的残余网络,再寻找新路径……直到某个残余网络上找不到从源到汇的路径为止,最大流就算出来了。
/*
*codevs1933 poj1273 题意
*现在有m个池塘(从1到m开始编号,1为源点,m为汇点),及n条水渠,给出这n条水渠所连接的点和
*所能流过的最大流量,求水渠中所能流过的水的最大容量。
*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int INF=0x7ffffff;
queue <int> q;
int n,m,x,y,s,t,g[201][201],pre[201],flow[201],maxflow;
//g邻接矩阵存图,pre增广路径中每个点的前驱,flow源点到这个点的流量
inline int bfs(int s,int t)
{
while (!q.empty()) q.pop();
for (int i=1; i<=n; i++) pre[i]=-1;
pre[s]=0;
q.push(s);
flow[s]=INF;
while (!q.empty())
{
int x=q.front();
q.pop();
if (x==t) break;
for (int i=1; i<=n; i++)
//EK一次只找一个增广路
if (g[x][i]>0 && pre[i]==-1)
{
pre[i]=x;
flow[i]=min(flow[x],g[x][i]);
q.push(i);
}
}
if (pre[t]==-1) return -1;
else return flow[t];
}
//increase为增广的流量
void EK(int s,int t)
{
int increase=0;
while ((increase=bfs(s,t))!=-1)//这里的括号加错了!Tle
{//迭代
int k=t;
while (k!=s)
{
int last=pre[k];//从后往前找路径
g[last][k]-=increase;
g[k][last]+=increase;
k=last;
}
maxflow+=increase;
}
}
int main()
{
scanf("%d%d",&m,&n);
for (int i=1; i<=m; i++)
{
int z;
scanf("%d%d%d",&x,&y,&z);
g[x][y]+=z;//此处不可直接输入,要+=
}
EK(1,n);
printf("%d",maxflow);
return 0;
}
#include<iostream>
#include<queue>
using namespace std;
const int N=201;
const int INF=99999999;
int n,m,sum,s,t,w;//s,t为始点和终点
int cap[N][N],a[N],p[N];
int min(int a,int b)
{
return a<=b?a:b;
}
void Edmonds_Karp()
{
int i,u,v;
queue<int>q;//队列,用bfs找增广路
while(1)
{
memset(a,0,sizeof(a));//每找一次,初始化一次
a[s]=INF;
q.push(s);//源点入队
while(!q.empty())
{
u=q.front();
q.pop();
for(v=1;v<=m;v++)
{
if(!a[v]&&cap[u][v]>0)
{
p[v]=u;
q.push(v);
a[v]=min(a[u],cap[u][v]);//s-v路径上的最小残量
}
}
}
if(a[m]==0)//找不到增广路,则当前流已经是最大流
break;
sum+=a[m];//流加上
for(i=m;i!=s;i=p[i])// //从汇点顺着这条增广路往回走
{
cap[p[i]][i]-=a[m];//更新正向流量
cap[i][p[i]]+=a[m];//更新反向流量
}
}
printf("%d\n",sum);
}
int main()
{
// freopen("in.txt","r",stdin);
int v,u;
while(scanf("%d%d",&n,&m)!=EOF)
{
s=1;//从1开始
t=m;//m为汇点
sum=0;//记录最大流量
memset(cap,0,sizeof(cap));//初始化
while(n--)
{
scanf("%d%d%d",&u,&v,&w);
cap[u][v]+=w;//注意图中可能出现相同的边
}
Edmonds_Karp();
}
return 0;
}
朴素算法的低效之处:
虽然说我们已经知道了增广路的实现,但是单纯地这样选择可能会陷入不好的境地,比如说这个经典的例子:
我们一眼可以看出最大流是999(s->v->t)+999(s->u->t),但如果程序采取了不恰当的增广策略:s->v->u->t
我们发现中间会加一条u->v的边
而下一次增广时:
若选择了s->u->v->t
然后就变成
这是个非常低效的过程,并且当图中的999变成更大的数时,这个劣势还会更加明显。
怎么办呢?
这时我们引入Dinic算法
Dinic算法
Edmonds-Karp算法,每进行一次增广,都要做 一遍BFS,十分浪费。能否少做几次BFS? 这就是Dinic算法要解决的问题
dinic算法在EK算法的基础上增加了分层图的概念,根据从s到各个点的最短距离的不同,把整个图分层。寻找的增广路要求满足所有的点分别属于不同的层,且若增广路为s,P1,P2…Pk,t,点v在分层图中的所属的层记为deepv,那么应满足deep(pi)=deep(pi−1)+1
Edmonds-Karp的提高余地:需要多次从s到t调用BFS,可以设法减少调用次数。 亦即:使用一种代价较小的高效增广方法。考虑:在一次增广的过程中,寻找多条增广路径。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int inf=1e9;
int n,m,x,y,z,maxflow,deep[500];//deep深度
struct Edge{
int next,to,dis;
}edge[500];
int num_edge=-1,head[500],cur[500];//cur用于复制head
queue <int> q;
void add_edge(int from,int to,int dis,bool flag)
{
edge[++num_edge].next=head[from];
edge[num_edge].to=to;
if (flag) edge[num_edge].dis=dis;//反图的边权为 0
head[from]=num_edge;
}
//bfs用来分层
bool bfs(int s,int t)
{
memset(deep,0x7f,sizeof(deep));
while (!q.empty()) q.pop();
for (int i=1; i<=n; i++) cur[i]=head[i];
deep[s]=0;
q.push(s);
while (!q.empty())
{
int now=q.front(); q.pop();
for (int i=head[now]; i!=-1; i=edge[i].next)
{
if (deep[edge[i].to]>inf && edge[i].dis)//dis在此处用来做标记 是正图还是返图
{
deep[edge[i].to]=deep[now]+1;
q.push(edge[i].to);
}
}
}
if (deep[t]<inf) return true;
else return false;
}
//dfs找增加的流的量
int dfs(int now,int t,int limit)//limit为源点到这个点的路径上的最小边权
{
if (!limit || now==t) return limit;
int flow=0,f;
for (int i=cur[now]; i!=-1; i=edge[i].next)
{
cur[now]=i;
if (deep[edge[i].to]==deep[now]+1 && (f=dfs(edge[i].to,t,min(limit,edge[i].dis))))
{
flow+=f;
limit-=f;
edge[i].dis-=f;
edge[i^1].dis+=f;
if (!limit) break;
}
}
return flow;
}
void Dinic(int s,int t)
{
while (bfs(s,t)){
int flow;
while(flow = dfs(s,t,inf))
maxflow += flow;
}
}
int main()
{
// for (int i=0; i<=500; i++) edge[i].next=-1;
memset(head,-1,sizeof(head));
scanf("%d%d",&m,&n);
for (int i=1; i<=m; i++)
{
scanf("%d%d%d",&x,&y,&z);
add_edge(x,y,z,1); add_edge(y,x,z,0);
}
Dinic(1,n);
printf("%d",maxflow);
return 0;
}
ISAP算法
ISAP(Improved Shortest Augmenting Path)(%ISA)也是基于分层思想的最大流算法。所不同的是,它省去了Dinic每次增广后需要重新构建分层图的麻烦,而是在每次增广完成后自动更新每个点的『标号』(也就是所在的层)
最短增广路算法是一种运用距离标号使寻找增广路的时间复杂度下降的算法。所谓的距离标号就是某个点到汇点的最少的弧的数量(即当边权为1时某个点的最短路径长度). 设点i的标号为d[i], 那么如果将满足d[i] = d[j] + 1, 且增广时只走允许弧, 那么就可以达到”怎么走都是最短路”的效果. 每个点的初始标号可以在一开始用一次从汇点沿所有反向的BFS求出。
GAP 优化
由于可行边定义为:(now,next) | h[now] = h[next]+1,所以若标号出现“断层”即有的标号对应的顶点个数为0,则说明剩余图中不存在增广路,此时便可以直接退出,降低了无效搜索。举个栗子:若结点标号为3的结点个数为0,而标号为4的结点和标号为2的结点都大于 0,那么在搜索至任意一个标号为4的结点时,便无法再继续往下搜索,说明图中就不存在增广路。此时我们可以以将 h[1]=n 形式来变相地直接结束搜索
//链式前向星存图
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
using namespace std;
const int inf=1e9;
queue <int> q;
int m,n,x,y,z,maxflow,head[5000],num_edge=-1;
int cur[5000],deep[5000],last[5000],num[5000];
//cur当前弧优化; last该点的上一条边; num桶 用来GAP优化
struct Edge{
int next,to,dis;
}edge[500];
void add_edge(int from,int to,int dis,bool flag)
{
edge[++num_edge].next=head[from];
edge[num_edge].to=to;
edge[num_edge].dis=dis;
head[from]=num_edge;
}
void bfs(int t) //逆向进行bfs更新deep
{
while (!q.empty()) q.pop();
for (int i=0; i<=m; i++) cur[i]=head[i];
for (int i=1; i<=n; i++) deep[i]=n;
deep[t]=0;
q.push(t);
while (!q.empty())
{
int now=q.front(); q.pop();
for (int i=head[now]; i!=-1; i=edge[i].next)
{
if (deep[edge[i].to]==n && edge[i ^ 1].dis) //i ^ 1是为了找反边
{
deep[edge[i].to]=deep[now]+1;
q.push(edge[i].to);
}
}
}
}
int add_flow(int s,int t)
{
int ans=inf,now=t;
while (now != s) //找最小的残量值
{
ans = min(ans, edge[last[now]].dis);
now = edge[last[now]^1].to;
}
now=t;
while (now!=s) //增广
{
edge[last[now] ].dis-=ans;
edge[last[now] ^ 1].dis+=ans;
now=edge[last[now]^1].to;
}
return ans;
}
void isap(int s,int t) //根据情况前进或者后退,走到汇点时增广
{
int now=s;
bfs(t); //搜出一条增广路
for (int i=1; i <= n; i++) num[deep[i]]++;
while (deep[s]<n)
{
if (now==t)
{ //如果到达汇点就直接增广,重新回到源点进行下一轮增广
maxflow += add_flow(s,t);
now = s; //回到源点
}
bool has_find=0;
for (int i = cur[now]; i != -1; i = edge[i].next)
{
if (deep[now] == deep[edge[i].to] + 1 && edge[i].dis) //找到一条增广路
{
has_find=true;
cur[now]=i; //当前弧优化
now=edge[i].to;
last[edge[i].to]=i;
break;
}
}
if (!has_find) //没有找到出边,重新编号
{
int minn=n-1;
for (int i=head[now]; i!=-1; i=edge[i].next) //回头找路径
if (edge[i].dis)
minn = min(minn, deep[edge[i].to]);
if ((--num[ deep[now] ])==0) break; //GAP优化 出现了断层
num[deep[now]=minn+1]++;
cur[now]=head[now];
if (now!=s)
now=edge[last[now]^1].to; //退一步,沿着父边返回
}
}
}
int main()
{
memset(head,-1,sizeof(head));
scanf("%d%d",&m,&n);
for (int i=1; i<=m; i++)
{
scanf("%d%d%d",&x,&y,&z);
add_edge(x,y,z,1); add_edge(y,x,z,0);
}
isap(1,n);
printf("%d",maxflow);
return 0;
}
//邻接表存图
#include<bits/stdc++.h>
using namespace std;
#define N 1000
#define INF 100000000
struct Edge
{
int from,to,cap,flow;
};
struct ISAP
{
int n,m,s,t;
vector<Edge>edges;
vector<int>G[N];
bool vis[N];
int d[N],cur[N];
int p[N],num[N];//比Dinic算法多了这两个数组,p数组标记父亲结点,num数组标记距离d[i]存在几个
void addedge(int from,int to,int cap)
{
edges.push_back((Edge){from,to,cap,0});
edges.push_back((Edge){to,from,0,0});
int m=edges.size();
G[from].push_back(m-2);
G[to].push_back(m-1);
}
int Augumemt()
{
int x=t,a=INF;
while(x!=s)//找最小的残量值
{
Edge&e=edges[p[x]];
a=min(a,e.cap-e.flow);
x=edges[p[x]].from;
}
x=t;
while(x!=s)//增广
{
edges[p[x]].flow+=a;
edges[p[x]^1].flow-=a;
x=edges[p[x]].from;
}
return a;
}
void bfs()//逆向进行bfs
{
memset(vis,0,sizeof(vis));
queue<int>q;
q.push(t);
d[t]=0;
vis[t]=1;
while(!q.empty())
{
int x=q.front();q.pop();
int len=G[x].size();
for(int i=0;i<len;i++)
{
Edge&e=edges[G[x][i]];
if(!vis[e.from]&&e.cap>e.flow)
{
vis[e.from]=1;
d[e.from]=d[x]+1;
q.push(e.from);
}
}
}
}
int Maxflow(int s,int t)//根据情况前进或者后退,走到汇点时增广
{
this->s=s;
this->t=t;
int flow=0;
bfs();
memset(num,0,sizeof(num));
for(int i=0;i<n;i++)
num[d[i]]++;
int x=s;
memset(cur,0,sizeof(cur));
while(d[s]<n)
{
if(x==t)//走到了汇点,进行增广
{
flow+=Augumemt();
x=s;//增广后回到源点
}
int ok=0;
for(int i=cur[x];i<G[x].size();i++)
{
Edge&e=edges[G[x][i]];
if(e.cap>e.flow&&d[x]==d[e.to]+1)
{
ok=1;
p[e.to]=G[x][i];//记录来的时候走的边,即父边
cur[x]=i;
x=e.to;//前进
break;
}
}
if(!ok)//走不动了,撤退
{
int m=n-1;//如果没有弧,那么m+1就是n,即d[i]=n
for(int i=0;i<G[x].size();i++)
{
Edge&e=edges[G[x][i]];
if(e.cap>e.flow)
m=min(m,d[e.to]);
}
if(--num[d[x]]==0)break;//如果走不动了,且这个距离值原来只有一个,那么s-t不连通,这就是所谓的“gap优化”
num[d[x]=m+1]++;
cur[x]=0;
if(x!=s)
x=edges[p[x]].from;//退一步,沿着父边返回
}
}
return flow;
}
};
int main()
{
// freopen("t.txt","r",stdin);
ISAP sap;
while(cin>>sap.n>>sap.m)
{
for(int i=0;i<sap.m;i++)
{
int from,to,cap;
cin>>from>>to>>cap;
sap.addedge(from,to,cap);
}
cin>>sap.s>>sap.t;
cout<<sap.Maxflow(sap.s,sap.t)<<endl;
}
return 0;
}
总结:
注意理解多路增广:虽然一个点要枚举所有出边,但实质仍然是 dfs,过程图类似于树。