网络流,一类听起来就很高大上的令无数OI选手胆颤的图论算法.
这里只讲解神奇的最大流问题.
最大流,就是一类在有向图上的问题.
这张有向图比较特殊,有一个源点,一个汇点.
且每条边都有一个容量.
最大流问题是指,从源点开始流,最多有多大的权值能流到汇点的一类图论问题.
网络图如下:
最大流其实就是把水灌入一条边之后,相当于把这条边的容量减少了,最终能流到的流量最大就是最大流问题的解.
我觉得我还是解释不清楚网络流,好好的给你们用公式说吧.
一张网络G={V,E},我们定义边(x,y)的权值为c(x,y),称为容量,且若不存在(x,y)∈E,则c(x,y)=0.且有两个节点S,T∈V,S称为源点,T称为汇点.
其中f(x,y)是一个流函数,表示边(x,y)的流量,且f(x,y)<=c(x,y),c(x,y)-f(x,y)为边的剩余容量.
整个网络流量为所有(S,v)∈E,f(S,v)的和.
整个网络流量的最大流量为最大流.
至于算法,我们这里介绍Karp算法.
karp算法比较简单的思想,就是一直不停地找增广路.
增广路的定义:网络图G中,从源点到汇点的一条路上最小容量边的容量>0简单路径.
karp算法就是不断找到增广路,找到一条后将整条路上流量最小的minf求出,增加到最大流的答案中,再将整条增广路上的剩余容量求出,继续跑.
一般来说karp算法的找增广路用bfs,因为bfs更加稳定.
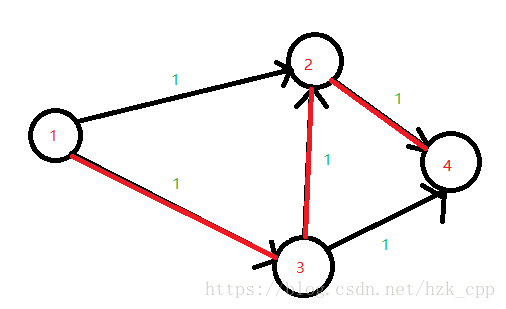
但是若真的直接这样模拟,会出问题,例如:
若直接沿着红色的路径走,最大流就是1,然而这张网络的最大流明显是2.
所以我们应该怎么处理呢?
若我们把反向边加进去:
那么就不会错了.
为什么呢?
因为我们这样相当于让程序有了一个反悔的机会.
通俗地说,就是你往反向边跑了过去,就相当于重新将这条边的容量给加回来了.
所以karp算法的代码如下:
struct queue{
int x,minf,last,edge;
}q[2*N+1];
bool use[N+1];
int h,t;
int bfs(int S,int T){
memset(use,0,sizeof(use));
h=t=1;
q[t].x=S;q[t].minf=INF;q[t].last=0;use[S]=1;
while (h<=t){
for (int i=lin[q[h].x];i;i=e[i].next)
if (!use[e[i].y]&&e[i].v){ //边必须还存在
use[e[i].y]=1;
q[++t].x=e[i].y;
q[t].minf=min(q[h].minf,e[i].v); //更新增广路上最小容量边的容量
q[t].last=h; //记录上一个状态的位置
q[t].edge=i; //记录边的编号
if (q[t].x==T) {
for (int j=t;q[j].last;j=q[j].last){ //更新增广路上的剩余容量
e[q[j].edge].v-=q[t].minf; //边的容量减小
e[q[j].edge^1].v+=q[t].minf; //反向边的容量增大
}
return q[t].minf; //返回这条增广路
}
}
++h;
}
return 0; //没有增广路,返回假
}
int maxflow(int S,int T){ //源点为S,汇点为T的最大流
int sum=0;
while (1){ //用while (1)控制循环
int minf=bfs(S,T); //做一遍bfs
if (minf) sum+=minf;
else break;
}
return sum;
}
注意,这种写法的成对储存要从第2条便开始存,也就是说,e[1]是不存在的.
时间复杂度O(n*m^2),但是上界很松,一般可以处理10^3~10^4级的数据.