网络流初步：最大流

标签：网络流最大流 Dinic

最大流

例题

POJ****（USACO4.2.1）

在农夫约翰的农场上，每逢下雨，Bessie最喜欢的三叶草地就积聚了一潭水。这意味着草地被水淹没了，并且小草要继续生长还要花相当长一段时间。因此，农夫约翰修建了一套排水系统来使贝茜的草地免除被大水淹没的烦恼（不用担心，雨水会流向附近的一条小溪）。作为一名一流的技师，农夫约翰已经在每条排水沟的一端安上了控制器，这样他可以控制流入排水沟的水流量。
农夫约翰知道每一条排水沟每分钟可以流过的水量，和排水系统的准确布局（起点为水潭而终点为小溪的一张网）。需要注意的是，有些时候从一处到另一处不只有一条排水沟。
根据这些信息，计算从水潭排水到小溪的最大流量。对于给出的每条排水沟，雨水只能沿着一个方向流动，注意可能会出现雨水环形流动的情形。

（题目描述似乎都点长？我自己再描述一下吧。）

1号点是池塘，n号点是小溪，还有m条沟渠（沟渠相交的地方就是其他节点）。沟渠，肯定有排水速率的上限，你可以调节每个沟渠的排水速率，使得池塘的排水速率最快。

（学完网络流之后，你可能会这样描述）

n个点m条边的网络，源点为1号点，汇点为n号点，求最大流。

最大流

结合题目的样例，可以画出这样一幅图：

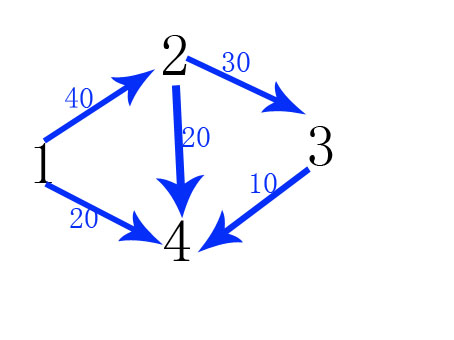
这道题目相当于求 1 -> 4 的最大流
诶？你都还没告诉我 最大流 是什么呢！

在容量网络中，满足弧流量限制条件，且满足平衡条件并且具有最大流量的可行流，称为网络最大流，简称最大流。
起点称为源点，终点称为汇点，每条边总是有一些奇怪的限制。
还是不懂怎么办？滑到最底下呗。

扫描二维码关注公众号，回复： 1904518 查看本文章

定义：从源点到汇点能流过的最大流量。
在图中，也就是从1号点到4号点的流量。

Dinic算法

Ford-Fulkerson方法

只要不断地在现有的流网络上累加小的流，当不能累加的时候就得到了最大流。
如果现有的流并不是最大流的一部分，是否还能累加形成最大流呢？
当然是可以的！

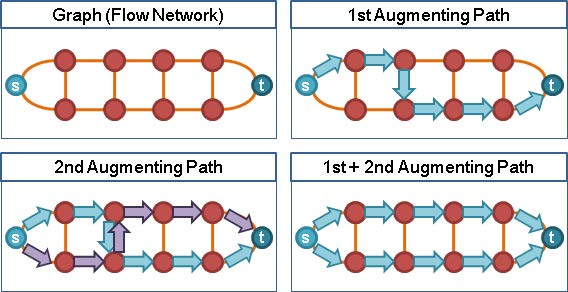
由于流具有方向性，并且相反方向的流互相抵消，我们可以发现，通过不同的流之间的叠加，我们可以通过回溯之前流的部分路段，从而修正之前的错误选择。

每次新增一条流的时候，我们都要满足每条边的容量限制。即当前这条边的流量加上新的流量，不能超过边的（剩余）容量限制。
一个便捷的处理方式是：记录这条边还能容纳的流量，即边的容量加上能够被回溯（对称边）的流量，称为“残存容量”。将所有的残存容量看成一个残存网络，也就是一个新的网络流问题，我们在新的图上继续寻找不饱和路径。

（说了那么多，其实就是找一条增广路(增广路在二分图匹配的时候就学完了吧？))

我们所需要做的就是记录每条边和它的反向边（对称性）以及每条边的剩余容量，写一个dfs每次寻找不饱和路径并修改容量，找不到时退出。此时我们得到了最大流。
使用最普通的深度优先搜索寻找增广路，每次时间复杂度为��(��)。设最大流的流量为��，由于每次流量至少增加1，时间复杂度为 ��(��)。
• 实际上，对于绝大多数的网络，该算法的运行
时间往往远远小于它的实际复杂度。

#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#define inf 1000000000
using namespace std;
bool eof=false;
int read(){
    int f=1,s=0;char c=getchar();
    if(c==(-1))eof=true;
    for(;c!=(-1)&&c<'0'||c>'9';c=getchar())if(c=='-')f=-1;
    for(;c>='0'&&c<='9';c=getchar())s=s*10+c-48;
    if(eof==true)return -1;
    return f*s;
}
struct qq{
    int u,v,flow,limit;
}a[410];
int n,m,s,t,cur[210],d[210];
bool b[210];
vector<int>f[210];
int dinic(int u,int limit){
    if(u==t||limit==0)return limit;
    int used=0,flow;
    for(int&i=cur[u];i<f[u].size();i++){    
        qq&e=a[f[u][i]];
        if(d[u]+1==d[e.v]){
            flow=dinic(e.v,min(limit,e.limit-e.flow));
            if(flow<=0)continue;
            a[f[u][i]].flow+=flow;
            a[f[u][i]^1].flow-=flow;
            used+=flow;
            limit-=flow;
            if(limit==0)break;
        }
    }
    return used;
}
bool bfs(){
    memset(b,0,sizeof(b));
    queue<int>q;int x,i;
    q.push(s);d[s]=0;b[s]=true;
    while(q.empty()==false){
        x=q.front();q.pop();
        for(i=0;i<f[x].size();i++){
            qq& e=a[f[x][i]];
            if(b[e.v]==false&&e.flow<e.limit){
                b[e.v]=true;
                d[e.v]=d[x]+1;
                q.push(e.v);
            }   
        }
    }
    return b[t]==true;
}
int maxflow(int ss,int tt){
    s=ss;t=tt;int flow=0;
    while(bfs()){
        memset(cur,0,sizeof(cur));
        flow+=dinic(s,inf);
    }
    return flow;
}
void work(){
    m=read();if(m==-1)return;
    n=read();int i,r=0,u,v,x;
    for(i=1;i<=n;i++)f[i].clear();
    for(i=0;i<m;i++){
        u=read();v=read();x=read();
        f[u].push_back(i*2);a[i*2]=(qq){u,v,0,x};
        f[v].push_back(i*2+1);a[i*2+1]=(qq){v,u,0,0};
    }
    printf("%d\n",maxflow(1,n));            
}
int main(){
    while(eof==false)work();
    return 0;
}

有兴趣/没听懂

网络流基本概念
最大流-最小割定理
更容易理解的Ford-Fulkerson思想
求解最大流的其他算法：Edmonds-Karp算法
求解最大流的其他算法：ISAP算法(Improved Shortest Augmenting Path)
求解最大流的其他算法：最高标号预流推进(HLPP)
网络流的其他东西：最小费用流等。

（番外）网络流基本概念

（整合，非原创：各种拼接，有待修改）

定义

有向图 $G=(V,E)$ 中：
有唯一的一个源点S( $V_s$ )（产地，出发点）
有唯一的一个汇点T( $V_t$ )（销地，结束点）
图中每条边 $(u,v)$ 都有一非负容量 $c(u,v)$
满足上述条件的图G称为网络流图（又称网络）。

容量网络

设 $G(V,E)$ ,是一个有向网络,在V中指定了一个顶点,称为源点(记为 $V_s$ ),以及另一个顶点,称为汇点(记为 $V_t$ );对于每一条弧 $<u,v>$ 属于E,对应有一个权值 $c(u,v)>0$ ,称为弧的容量。通常吧这样的有向网络G称为容量网络。

弧的流量

通过容量网络G中每条弧

网络流

所有弧上流量的集合 $f={f(u,v)}$ ,称为该容量网络的一个网络流.
可行流:在容量网络G中满足以下条件的网络流f,称为可行流.
a.弧流量限制条件: $0<=f(u,v)<=c(u,v)$ ;
b:平衡条件:即流入一个点的流量要等于流出这个点的流量,(源点和汇点除外).
若网络流上每条弧上的流量都为0,则该网络流称为零流.

伪流

如果一个网络流只满足弧流量限制条件,不满足平衡条件,则这种网络流为伪流,或称为容量可行流.(预流推进算法有用)

最大流

在容量网络中,满足弧流量限制条件,且满足平衡条件并且具有最大流量的可行流,称为网络最大流,简称最大流.

弧的类型:

a.饱和弧:即 $f(u,v)=c(u,v)$ ;
b.非饱和弧:即 $f(u,v)<c(u,v)$ ;
c.零流弧:即 $f(u,v)=0$ ;
d.非零流弧:即 $f(u,v)>0$ 。

链

在容量网络中,称顶点序列 $(u1,u2,u3,u4,\dots,un,v)$ 为一条链要求相邻的两个顶点之间有一条弧.
设P是G中一条从 $Vs$ 到 $Vt$ 的链,约定从Vs指向Vt的方向为正方向.在链中并不要求所有的弧的方向都与链的方向相同.
a.前向弧:(方向与链的正方向一致的弧),其集合记为P+,
b.后向弧:(方向与链的正方向相反的弧),其集合记为P-.

增广路

设f是一个容量网络G中的一个可行流,P是从 $V_s$ 到 $V_t$ 的一条链,若P满足以下条件:
a.P中所有前向弧都是非饱和弧,
b.P中所有后向弧都是非零弧.
则称P为关于可行流f 的一条增广路.
沿这增广路改进可行流的操作称为增广.

残留容量

给定容量网络G(V,E),及可行流f,弧

残留网络

设有容量网络G(V,E)及其上的网络流f,G关于f的残留网络记为G(V’,E’)。其中G’的顶点集V’和G中顶点集G相同,V’=V.对于G中任何一条弧