初识网络流(Ford-Fulkerson算法，Edmonds-Karp 最短增广路算法，Dinic 快速网络流算法)

今天！蒻终于知道了什么是网络流！！
对于一个源点和一个汇点，之间有许多条有一定容量的边，问单位时间内从源点到汇点最多可以流过多少流量。

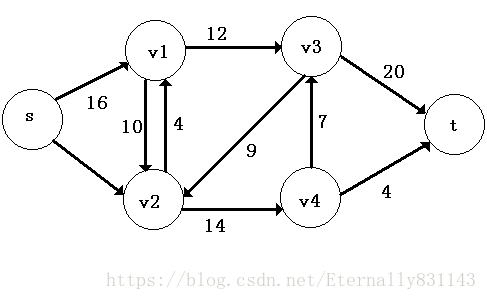
就拿这张图来说，就是问从源点$s$到汇点$t$单位时间内的最大流量。
那对于最大流问题，有什么解决方法呢？

Ford-Fulkerson算法

基本思想就是每次用$dfs$从源点开始搜索，直到汇点停止，这之间所经过的边中容量最小的一条边就是每次次$dfs$所搜索到的容量，然后每次在搜索到汇点之后，对于路径上的每条边，都要减去本次搜索到的流量，最后直到找不到可行路径，每次$dfs$搜索到的流量加起来就是从源点到汇点的最大流。但是这样做是存在一些问题的 。

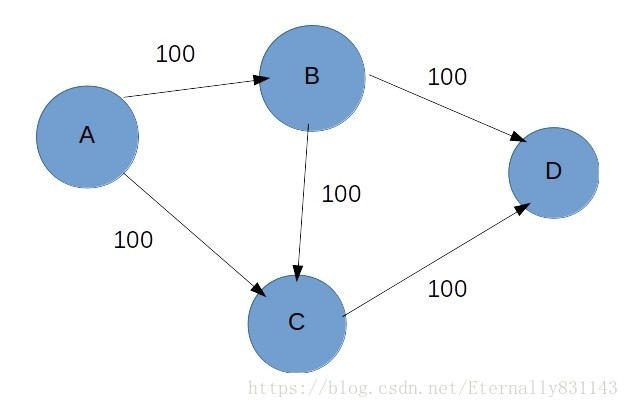
就拿这个图来说，如果我们从$A\to B\to C\to D$这样走的话，我们最终得到的最大流只能是$100$，但是实际上我们可以走$A\to B\to D$和$A\to C\to D$这两条，这样最大流就是$200$。所以说，我们只是简单$dfs$的话，我们就有可能过早的认为$B\to C$流量不为$0$，因而在一次$dfs$之后将$B\to C$变为了$0$，使得$dfs$找不到可行路了。所以改进方法就是在每次$dfs$之后给路径的每一条边加一条反向边。反向边的容量和上次$dfs$刚找到这条边时的容量相等。这样我们就可以利用这条反向边和剩余的边继续寻找可行路。(至于为何添加反向边这种操作是正确有效的，日后有时间再补，(^__^) 嘻嘻……)

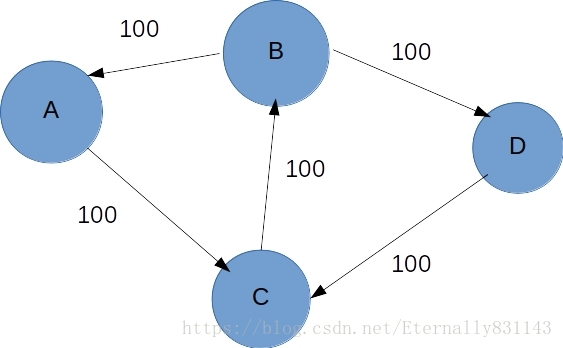
添加反向边之后我们就可以走$A\to C\to B\to D$这条路，然后总流量就变为了$200$，再次添加反向边，就没有可行路了，所以算法结束，最大流为$200$。

但是，这种算法同样存在缺陷，就是对于下面这张图

我们最坏可能要进行$200$次$dfs$，因为只要走$B\to C$这条路，就算添加反向边，每次总流量也只是添加$1$而已。
算法复杂度为$C*(m+n)=C*n^2$，$C$为$dfs$运行次数，$m$为边数，$n$为顶点数。

Edmonds-Karp 最短增广路算法

这种算法很好的避免了上述情况，每次找可行路增广时，选择从源点到汇点具有最少边的路径，利用$bfs$找增广路径。

Dinic 快速网络流算法

上一种算法，每次增广的时候都要进行一次$bfs$，$Dinic$算法又很好的优化了这个算法，在每一次进行增广的时候，用$dfs$寻找多条增广路。

首先，利用$bfs$对残余网络进行分层，

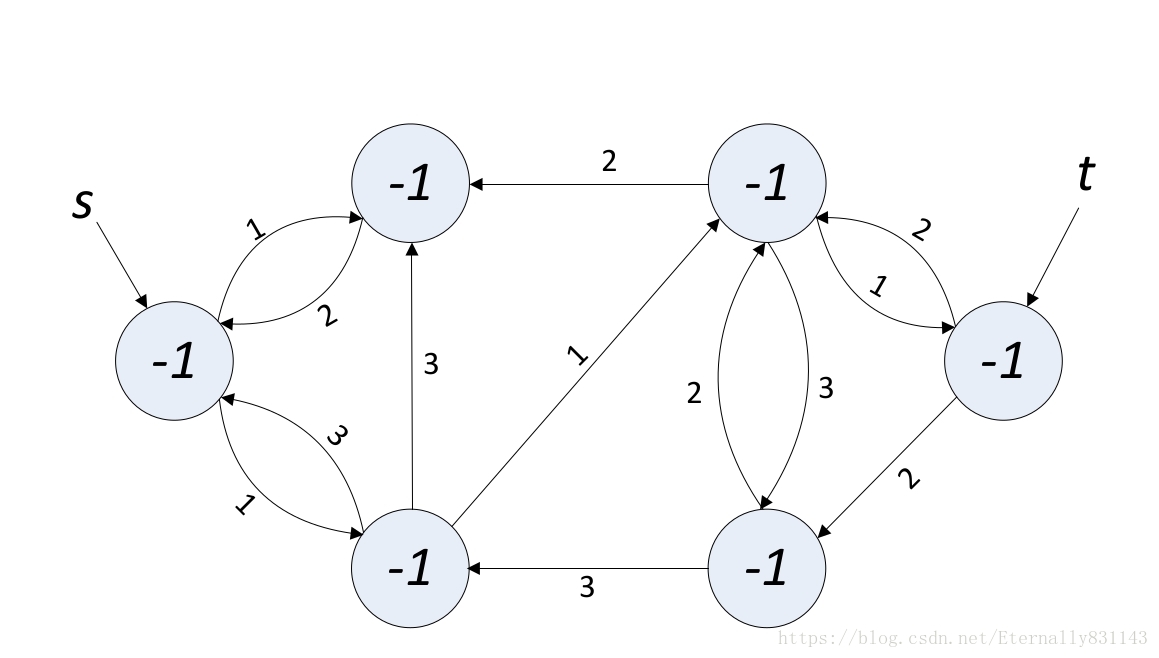
一个节点的层数就是源点到它需要经过的最少边数。

在分层完毕之后，利用$dfs$做我们前面说的寻找增广路径，增加总流量的值，并且消减路径各边的容量，添加反向边。但是，前面每次碰到汇点之后就停止了，这里我们并不立即停止，而是进行回溯，我们应该回溯到哪个节点呢？我们应该回溯到的节点必须是$dfs$搜索树中边$(u,v)$的容量为$0$并且最上层的节点。
为什么？
因为$dfs$找到增广路径添加反向边消减路径各边容量之后，有些边可能就为$0$了，如果我们回溯到的不是最上层，那么我们再次进行$dfs$找出的增广路径所增加的流量一定是$0$！你们猜是否会找不到容量为$0$的边呢？一定会的！想一下，我们前面每次$dfs$所增加的流量，是由增广路径中容量最小的一条边决定的，所以说我们消减容量的话，一定会将增广路径中那条容量最小的边容量变为$0$，因此我们一定可以找到这条边。
如果$dfs$回溯到源点，并且无法往下走的时候，$dfs$结束。
$dfs$结束之后，再次用$bfs$对残余网络进行分层，直到分层操作无法算出汇点的层次之后(即$bfs$无法到达汇点时)，算法结束，最大流求出。
$Dinic$复杂度是 $n*n*m$ $(n$是点数，$m$是边数$)$。

靴靴各位巨巨观看！蒻初学，若有错误还请指出！^_^
（本文图片均来自于在PKU暑期上课期间的PPT）