数论——最大公约数

最大公约数

最大公约数即为 Greatest Common Divisor，常缩写为 gcd。

欧几里得算法

证明过程

代码实现

int gcd(int a, int b) {
  if (b == 0) return a;
  return gcd(b, a % b);
}

如果两个数a 和 b满足gcd(a,b)=1 ，我们称 a和 b互质。

Steim算法

二进制来求最大公约数

欧几里德算法是计算两个数最大公约数的传统算法，无论从理论还是从实际效率上都是很好的。但是却有一个致命的缺陷，

这个缺陷在素数比较小的时候一般是感觉不到的，只有在大素数时才会显现出来。

算法应用的结论：

1.gcd(a,a)=a，也就是一个数和其自身的公约数仍是其自身。

2.gcd(ka,kb)=k gcd(a,b)，也就是最大公约数运算和倍乘运算可以交换。特殊地，当k=2时，说明两个偶数的最大公约数必然能被2整除。

3.当k与b互为质数，gcd(ka,b)=gcd(a,b)，也就是约掉两个数中只有其中一个含有的因子不影响最大公约数。特殊地，当k=2时，说明计算一个偶数和一个奇数的最大公约数时，可以先将偶数除以2。

代码实现

#define　CHECK(a)　(!(1&(a)))//判断是否被2整除
#define　CLEAN2(a)　while(CHECK(a))a=a>>=1//移除非公因子的2
#define　BIGERA　if(a<b)(t=a,a=b,b=t)//取较大的数为a
int　gcd(int　a,int　b){
　int　c_2=0,t;
　while((CHECK(a))&&(CHECK(b))){
　a=a>>=1;b=b>>=1;c_2++;
　}
　CLEAN2(a);
　CLEAN2(b);
　BIGERA;
　while(a=((a-b)>>1)){
　CLEAN2(a);
　BIGERA;
　}
　return　b<<c_2;
}

两种算法的比较：

欧几里德算法每次迭代中最恶劣的情况是，a=2b-1，这样，迭代后，r=b-1。如果a小于2^N，这样大约需要4N次迭代。而Stein算法，每次迭代后，显然AN+1BN+1≤ ANBN/2，最大迭代次数也不超过4N次。也就是说，迭代次数几乎是相等的。但是，需要注意的是，对于大素数，试商法将使每次迭代都更复杂，因此对于大素数，Stein算法将更有优势。

最小公倍数

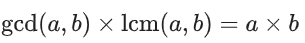
利用该结论可得出。

扩展欧几里得定理

扩展欧几里德定理（Extended Euclidean algorithm, EXGCD），常用于求ax+by=gcd(a,b)的一组可行解。

证明过程

int Exgcd(int a, int b, int &x, int &y) {
  if (!b) {
    x = 1;
    y = 0;
    return a;
  }
  int d = Exgcd(b, a % b, x, y);
  int t = x;
  x = y;
  y = t - (a / b) * y;
  return d;
}

函数返回的值为 GCD，在这个过程中计算x,y即可。

数论——最大公约数

猜你喜欢