【LeetCode 300】最长上升子序列
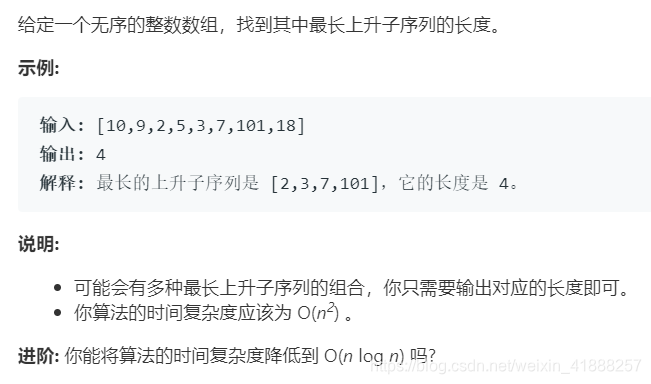
1. 题目描述
原题: 【LeetCode 300】.
2. 解题思路
动态规划的思想核心类似于数学归纳法。
即通过n-1,n-2来推导n
常见的具体做法是,建立一个dp-table,即一个一维dp数组或者二维dp数组,将递归转化为递推,把大问题分解成子问题,而后通过边界值,再从最小的子问题开始,将dp表依次填满。最终答案就在dp表中。
2.1找子问题
求序列的前n个元素的最长上升子序列的长度 是个子问题,但这样分解子问题,不具有“无后效性”。
假设F(n) = x,但可能有多个序列满足F(n) = x。有的序列的最后一个元素比 an+1小,则加上an+1就能形成更长上升子序列;有的序列最后一个元素不比an+1小……以后的事情受如何达到状态n的影响,不符合“无后效性”。(关于"无后效性"可参考: 无后效性.)
具体举例说明“无后效性”
index = 0 1 2 3 4 5 6
nums = [1,6,9,3,4,5,7]
前5个元素 (1,6,9,3,4)的最长上升子序列是 1,6,9或者1,3,4.但是加上第6个元素“5”以后,即前6个元素的最长上升子序列长度可能是3(1,6,9),也可能是4 (1,3,4,5)。也就是前5个元素的最长上升子序列长度会直接影响前6个元素的最长上升子序列长度,即无后效性。
所以子问题应该换成
以序列的第n个元素为终点的最长上升子序列的长度
这样一来,上述例子中第5个元素为终点的最长上升子序列,限定了只有一种可能即 长度为3的 (1,3,4),(直观地看就是具有了唯一性)那么终点为第6个元素的最长上升子序列是长度为4的(1,3,4,5)。
2.2 从简单问题入手
复杂的数学问题,往往总是从简单的问题入手,从具体到抽象,一步步解决的。先举个简单的例子:
nums = [1,3,6,7,9,4,10,5,6]
dp表 = [1,2,3,4,5,3, 6, 4,5]
从上述例子可以简单得出以下结论:
- dp表的最小值为1,也就是最短就是本身
- dp[i] = nums[0],…,nums[i-1]之中所有小于nums[i]的值的最大值所对应的dp值 + 1
换句话说,即 dp[i] = nums[0],…,nums[i-1]之中最接近nums[i]的值(假设为nums[j])所对应的dp值(假设为dp[j]) + 1
2.3 代码
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
"""O(n^2)的时间复杂度"""
L = len(nums)
if L == 0:
return 0
dp = [1] * L
for i in range(1, L):
for j in range(0, i):
if (nums[j] < nums[i]): # 上升
# temp = dp[j] + 1
# if dp[i] < temp:
# dp[i] = temp
# 以上三行可以化简为:
dp[i] = max(dp[i], dp[j] + 1)
#print(dp)
return max(dp)