2020.02.02日常总结——有趣的例题讲解

$\color{green}{一本通1478：The\ xor-longest\ Path}$

$\color{blue}{【题意】：}$ 输入一棵 $n$个点的 $\color{red}{带权树}$（即每条边有边权的树），求树上最长异或路径。

$\color{blue}{【数据范围】：}$ 记 $w$为边权，则有 $1\leq w < 2^{31}$。 $1 \leq n \leq 1 \times 10^5$，且所有的点从 $1$到 $n$编号。

$\color{blue}{【思路】：}$ 像这种，求树上路径的异或和或长度和等等可以利用前缀和算法维护的信息时，我们一般都要用到树上前缀和算法。

具体地，我们可以记 $d_i$表示从根（无根树吗，随便找个点当根得了，我们就当它是 $1$吧）到 $i$的路径异或和。根据异或的性质，两点 $(x,y)$间路径的异或和即 $d_x$异或 $d_y$。

于是，我们可以把所有的 $d_i(1 \leq i \leq n)$都求出来，然后把它们塞进一棵Trie内，问题就转化为了求两两数之间的异或最大值。这是一个Trie的简单应用题，这里不在介绍。

$\color{blue}{【代码】：}$

const int N=1e5+100;
struct Tire{
	int ch[N*30][2],tot;//千万别只开ch[N][2]
	void init_trie(){
		memset(ch,-1,sizeof(ch));
		tot=0;
	}
	void insert(int x){
		register int u=0;
		for(int i=30;i>=0;i--){
			int c=x&(1<<i)?1:0;
			if (ch[u][c]==-1)
				ch[u][c]=++tot;
			u=ch[u][c];
		}
	}
	int query(int x){
		register int u=0,ans=0;
		for(int i=30;i>=0;i--){
			int c=x&(1<<i)?1:0;
			if (ch[u][1-c]!=-1){
				ans+=(1<<i);
				u=ch[u][1-c];
			}
			else u=ch[u][c];
		}
		return ans;
	}
}trie;//封装一个Trie的模板
struct node{
	int next,to,value;
}e[N<<1];int h[N],tot;
inline void add(int a,int b,int w){
	e[++tot]=(node){h[a],b,w};h[a]=tot;
}//链式前向星存图
int d[N],ans,n;
void dfs_init(int u,int fa){
	for(int i=h[u];i;i=e[i].next){
		register int to=e[i].to;
		if (to==fa) continue;
		d[to]=d[u]^e[i].value;
		dfs_init(to,u);
	}
}//求前缀异或和
int main(){
	n=read();ans=-1;
	trie.init_trie();//记得要初始化
	for(int i=1;i<n;i++){
		int u=read(),v=read(),w=read();
		add(u,v,w);add(v,u,w);
	}//因为是无根树，所以最好建立无向图
	dfs_init(1,-1);//别忘了调用
	for(int i=1;i<=n;i++){
		trie.insert(d[i]);
		ans=max(ans,trie.query(d[i]));
	}//先后顺序无所谓
	printf("%d",ans);
	return 0;
}

---

$\color{green}{洛谷P2261\ \ \ [CQOI2007]余数求和}$

$\color{blue}{【题意】：}$ 给定 $N,K$，求（ $\%$表示求余）：
$\sum^{N}_{i=1} K \%i$

$\color{blue}{【数据范围】：}$ $1 \leq N,K \leq 1 \times 10^9$。

$\color{blue}{【思路】：}$ 首先，我们来看看计算机是怎么计算求余的结果的。假设现在要求 $P \% Q$，结果为 $X$，我们的计算机会这么算：

$X=P-Q \times \lfloor \frac{P}{Q} \rfloor$

这给我们什么启示？我们发现 $\lfloor \frac{P}{Q} \rfloor$变化的特别慢，至多会变化 $\sqrt P$次， $\sqrt{1 \times 10^9}<1 \times 10^5$，而且所有令 $\lfloor \frac{P}{Q} \rfloor$不变的 $Q$是连续的，我们完全可以考虑所有的 $\lfloor \frac{P}{Q} \rfloor$的值，然后统计答案。

$\color{blue}{【代码】：}$

$\color{blue}{【后记】：}$ 我们发现代码非常的简单，但也非常的不好理解，尤其是那个for循环。这里，我们简单讲讲。

它的作用是求出最大的 $r$，使得 $\lfloor \frac{k}{l} \rfloor=\lfloor \frac{k}{r} \rfloor$，根据它的特有的性质，我们可以知道对于任意 $i(l \leq i \leq r)$，有 $\lfloor \frac{k}{i} \rfloor=\lfloor \frac{k}{l} \rfloor=\lfloor \frac{k}{r} \rfloor$。

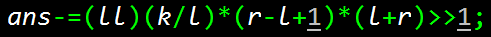
这个减号是什么意思？其实是这样的，因为 $X=P-Q \times \lfloor \frac{P}{Q} \rfloor$，所以我们可以把所求式转化为：

$\sum^{N}_{i=1} K \% i=\sum^{N}_{i=1} K-i \times \lfloor \frac{K}{i} \rfloor=N \times K - \sum^{N}_{i=1} i \times \lfloor \frac{K}{i} \rfloor$

因为上文已经说道 $\lfloor \frac{K}{i} \rfloor$都一样，所以原式可以继续变形为：

$原式=N \times K-(\sum\limits_{i=1}^{N} i) \times \lfloor \frac{K}{l} \rfloor$

这样就不难理解为什么我们有这么一段代码了吧。

Q：实在不能理解怎么办？
A：自己举个例子，模拟一下。例子可以很好的帮助我们理解。
Q：数论题自己想不到，但一看题解就懂是怎么回事？
A：您这种情况跟笔者一模一样，笔者只能说：多刷题吧！
Q：您这些思路怎么来的？我怎么一开始没想到？
A：您好，我一开始也没想到，思路全部来自题解或老师的讲解。