基于传染病引发的概率问题（独立概率和条件概率）

概要：

昨天工作群发了一个关于传染病的感染感染概率问题，整个群都炸了，策划，后端，前端，测试各自用自己的思维尝试给这个问题一个正确的答案。当然了，我也加入其中了，不过结果却，emmm，让我开始怀疑自己是不是不太适合做一个程序员。

问题：

讨论结果:

最终讨论结果我觉看起来比较靠谱的大概有两个：

• 52.734375%

计算思路

• 50%

计算思路

我们最后在讨论究竟哪个才是正确答案，我们想要解决这个问题就一定要了解概率的一些基本概念，下面简单介绍一下概率的一些需要了解的一些东西。

概率

定义

概率，亦称“或然率”，它是反映随机事件出现的可能性（likelihood)大小。随机事件是指在相同条件下，可能出现也可能不出现的事件。例如，从一批有正品和次品的商品中，随意抽取一件，“抽得的是正品”就是一个随机事件。设对某一随机现象进行了n次试验与观察，其中A事件出现了m次，即其出现的频率为m/n。经过大量反复试验，常有m/n越来越接近于某个确定的常数（此论断证明详见伯努利大数定律）。该常数即为事件A出现的概率，常用P (A) 表示。

 概率论中独立事件的讨论

开始之前，我们要明确描述一个问题的概率问题时，必须准确把握这个"样本空间"，概率书上一般称这个为所有可能的结果构成的集合为"样本空间"。如果甲在描述的一个问题的样本空间为A,它基于这个A的出一个概率，而乙在另外一个不同的样本空间B中得出一个概率，那么讨论和的关系需要谨慎，要不然就是驴唇不对马嘴。

1. 条件概率

学习条件概率的时候会碰到下面的条件概率公式：

                      

这个式子的意思就是F事件发生的条件下，E事件发生的概率。从字面上，主观的感受觉这个是很容易被理解的一个公式。要深刻理解这个条件公式概率的话，是需要深刻理解这里面讨论概率问题时"样本空间"的切换。用“维恩图”来理解更容易掌握实质：

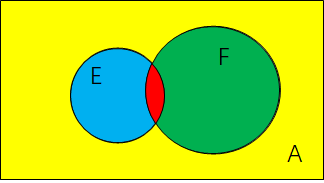
，即条件概率P(E|F)等于红色部分面积（EF相交部分面积）除以F事件面积（绿色+红色面积）

也就是说求时候的样本空间是以F事件的样本空间为参考的，这与（即F事件面积除以A原始样本空间面积）。

也就是说和两个概率所参考的样本空间完全不一样：

是基于原始样本空间A，是基于新的样本空间F。

2. 事件独立

定义：对于事件E和事件F,如果满足下面的公式，那么称它们是独立的。若两个事件E和F不独立，则称它们是相依的，或者相互不独立。

因此如果事件E和事件F独立，那么肯定满足下满的式子：

观察上面的维恩图，可知:

这也就说明了事件F的样本空间对事件E样本空间的切割后这部分(即形成维恩图中红色部分空间)在F中的比例和事件E在原来总体样本空间A中的比例是一致的，实际上这种"同比例切割"的特性，是确定F与E是否独立的一个标志，如果F事件样本空间同比例切割E事件空间，那么E和F就是独立的。这样子的描述和"F事件的发生并不影响E发生的概率，那么E和F就是独立的", 事实上这样子的描述在主观上有时候不是特别容易判断的。用"同比例切割"有时候更容易判断两个事件是否是独立的。相反的，不能同比例切割的话，那可以判断E和F是不独立的。

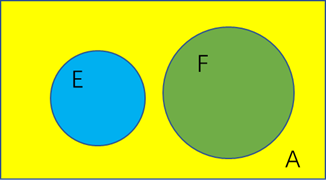
利用这个结论，观察上面这个维恩图，它告诉我们，E和F事件没有相交的部分，按照"同比例切割"的观点，F事件和E事件是"不独立"的！ 当然也可以利用是否满足公式方式去验证独立性。 这个图告诉我们：

两个不相交的事件，反而是"相互不独立"的。除了一种情况，事件E不可能出现，也就是P(E)=0。

这给我们一种新的认识：世界上两个没有任何交集的人，却相互不独立。除非你不存在。

造成这种错觉的原因是，讨论问题的角度不一样，相交讨论的是两个事件的集合，而"独立性"与否讨论的是比例(也就是概率)的问题。另外，概率论中的"独立"都是特别针对概率值的影响的，而人的独立性讨论的是人格特征。概率论中只是借用了"独立"这个词，概念上被赋予了严格的数学意义。

例1. 从一副洗好的52张扑克牌里随机抽取一张牌，令E表示事件"抽取的牌为一张A"，令F表示事件"抽取的牌为一张黑桃"，那么E和F就是独立的。因为P(EF)=1/52，而P(E)=4/52且P(F)=13/52。

这个例子也可以用"同比例分割"的方法来判断。原始样本空间大小为52，事件E空间大小有4（因为有4张牌A），因此事件E在原来空间中的分割比例时4/52。 相交事件EF样本空间（既是牌A又是黑桃）1，事件F的样本空间很明显是13（因为有13张黑桃），因此，EF在F中的分割比例为1/13。4/52=1/13，因此是独立的。

例2. 掷两枚均匀的骰子，令表示事件"骰子点数和为6"，令F表示事件"第一枚骰子点数为4"，那么

而

因此，和F不独立。也可以用"同比例分割"法。E1F相交事件在F中分割的比例为1/6，而E1事件在原来空间的比例是5/36。

例2, 如果令表示事件"骰子点数和为7",那么F和是独立的。请自证。

需要强调的是，两个事件独立并不代表两个事件之间没有影响，影响这个词太笼统了，因为，影响这个词没有说具体什么影响。而概率论中，事件之间是否独立，它强调的是事件F的出现与否对事件E原来发生的概率是否有影响！它明确了影响什么！即便事件F对事件E产生其他影响，只要不影响E的概率，那就是"独立"！

结果

最终结果是：d被感染的概率是50%

讨论结果一错误的原因是：

当bc互相握手后，b和c感染的概率都是62.5%（50%的概率是bc全都感染，12.5%的概率是bc只感染一个），此时62.5%中的50%和12.5%的采样空间是不一致的，必须分来计算与d握手时，d被感染的概率。

所以讨论结果一的第三步是错的。
————————————————
版权声明：本文为CSDN博主「皮皮君」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_16587307/article/details/89415118