联合概率及其分布、边缘概率及其分布、条件概率及其分布和贝叶斯定理

版权声明：站在巨人的肩膀上学习。 https://blog.csdn.net/zgcr654321/article/details/85201614

联合概率及其分布、边缘概率及其分布、条件概率及其分布

联合概率与联合概率分布

假设有随机变量X与Y, 此时，P(X=a,Y=b)用于表示X=a且Y=b的概率。这类包含多个条件且所有条件同时成立的概率称为联合概率。联合概率并不是其中某个条件的成立概率， 而是所有条件同时成立的概率。

联合概率的一览表称为联合分布。

边缘概率与边缘概率分布

P(X=a)或P(Y=b)这类仅与单个随机变量有关的概率称为边缘概率。

边缘概率的一览表称为边缘分布。

条件概率与条件概率分布

在条件Y=b成立的情况下，X=a的概率，记作P(X=a|Y=b)或P(a|b)。

若只有两类事件X和Y，那么有

$\mathrm { P } ( X = a | Y = b ) = \frac { \mathrm { P } ( X = a , Y = b ) } { \mathrm { P } ( Y = b ) }$

条件概率的分布简称条件分布，即已知两个相关的随机变量X和Y，随机变量Y在条件{X=x}下的条件概率分布是指当已知X的取值为某个特定值x之时，Y的概率分布。

举例：

扑克牌的花色及X、Y的联合分布如下所示。

下面我们来计算条件概率。上面的图可以进一步表示为：

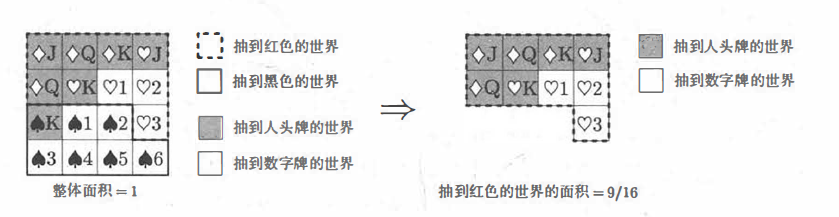
首先我们要知道：

P(Y=数字牌|X=红色)+P(Y=人头牌|X=红色)=1

用公式可表示为：

$\sum _ { b } \mathrm { P } ( Y = b | X = a ) = 1$

由上图，我们可以知道"X=红色” 的世界中有三分之一的"Y=数字牌” ， 三分之二
的"Y=人头牌” 。故我们就可以得到相应的条件概率公式：

P(Y=数字牌|X=红色)=1/3

P(Y=人头牌|X=红色)=2/3

即在条件X=红色成立时，Y=数宇牌的条件概率是1/3；在条件X=红色成立时，Y=人头牌的条件概率是2/3。

联合概率、边缘概率、条件概率之间的关系

“XY的联合概率”=“X基于Y的条件概率”乘以“Y的边缘概率” 。

离散型分布的情况

离散型分布下联合概率、边际概率、条件概率之间的等式关系：

$\operatorname { P } ( X = x ) = \sum _ { y } \operatorname { P } ( X = x , Y = y ) = \sum _ { y } \operatorname { P } ( X = x | Y = y ) \operatorname { P } ( Y = y )$

$\mathrm { P } ( X = x , Y = y )$为XY的联合概率， $\mathrm { P } ( X = x )$为X的边际概率， $\mathrm { P } ( X = x | Y = y )$ 为X基于Y的条件概率， $\mathrm { P } ( Y = y )$为Y的边际概率。

连续型分布的情况

$P _ { X } ( x ) = \int _ { y } P _ { X , Y } ( x , y ) \mathrm { d } y = \int _ { y } P _ { X | Y } ( x | y ) P _ { Y } ( y ) \mathrm { d } y$

只需要将“累加”换成“积分”，就是连续型分布下联合概率、边际概率、条件概率之间的转换计算公式。

贝叶斯定理(贝叶斯公式)

先验概率

事件发生前的预判概率。可以是基于历史数据的统计，可以由背景常识得出，也可以是人的主观观点给出。一般都是单独事件概率，如P(X),P(Y)。

后验概率

事件发生后求的反向条件概率；或者说，基于先验概率求得的反向条件概率。概率形式与条件概率相同。

贝叶斯公式

设X和Y分别为两类不同的事件，假设X和Y是互相独立的(属性条件独立性假设)，由公式

$p ( X | Y) p ( Y ) = p ( X , Y ) = p ( Y | X ) p ( X )$

我们可以得到贝叶斯公式：

$p ( Y | X ) = \frac { p ( X | Y ) p ( Y ) } { p ( X ) }$

其中：

• P(Y|X)是后验概率，一般是我们求解的目标。表示当拥有X这个条件后Y的概率，由于有X这个条件，后验概率可能与先验概率不同；

• P(X|Y)是条件概率，又叫似然概率，它表示在承认先验的条件下另一个与之相关的随机变量的表现，一般是通过历史数据统计得到（即通过一个已知的小样本统计得到）。

• P(Y) 是先验概率，它表示我们对一个随机变量概率最初的认识，一般都是人主观给出的。贝叶斯中的先验概率一般特指它。

• P(X)其实也是先验概率，只是在贝叶斯公式中往往被认为是已知的，因此它一般被当做一个常量看待。使用朴素贝叶斯分类器计算时往往忽略这个P(X)，因为它是常量。

使用加法规则，则贝叶斯定理中的分母可以用出现在分子中的项表示：

$p ( X ) = \sum _ { Y } p ( X | Y ) p ( Y )$

我们可以把贝叶斯公式的分母p(x)看做归一化常数，来确保贝叶斯公式左侧的条件概率对于所有的Y的取值之和为1。