
3.1 基本形式
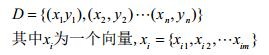
一般用向量形式写成
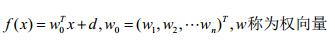
本文介绍几种经典的线性模型,看我们先从回归任务开始,然后讨论二分类和多分类任务。
3.2 线性回归
线性回归是一种监督学习下的线性模型,线性回归试图从给定数据集中学习一个线性模型来较好的预测输出
(可视为:新来一个不属于D的数据,我们只知道他的x,要求预测y,D如下表示)。
作为一个程序猿,数学功底是很重要的,偏偏本人线数遗忘很多,简单的写一下推导过程。
为了便于后文分析,我们将d归并到w中:
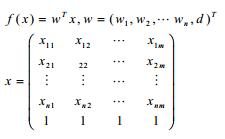
现在,输入,目标函数,输出都有了。我们要想要好的预测y,那么我们首先应该在D上f(x)要能够表现的比较满意,即当D中任意一个(xi,yi),将xi带入f(x),最后得出的f(xi)≈yi,当然某些情况除外,比如离群点,这些点可能本身受噪声影响太大,或者本身就是个错误的数据。要衡量f(xi)是否约等于yi,我们可以定义f(xi)与yi之间的均方误差,这种误差非常直观,它实际上也可以看成是欧几里得空间的距离计算。
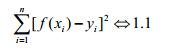
上述分析是从直观上的结果,我们必须要用代数的方式来表示f(xi)与yi之间的进阶程度;这实际上是对1.1的一个优化问题。即寻找一组(w,b)使得1.1式的值足够小,使用矩阵对1.1式进行表达:
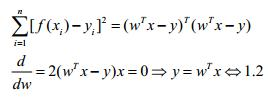
根据线性方程组有解的条件,由于x,y是任意的,因此我们无法判断方程是否有解。分以下情况讨论:
(1)y=wTx满足有解条件,即R(wTx)=R(wTx|y)。此时可以直接解除w。
(2)y=wTx无解,但肯定存在最小二乘解:
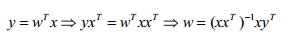
此时最终学到的模型为:
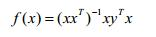
3.3 对数几率回归
对于这个logistic回归,先说两点容易误解的地方:
一是他是一种线性模型,针对权向量w的线性模型;
二是虽然他的名字带有回归,但他是如假包换的分类算法。
Logistic回归实际是在线性回归的基础上引入一个函数将原先的回归转化为分类。
考虑二分类任务:
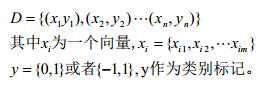
有了数据集及类别标记,那么我们可以将上文中线性模型的结果与类别label通过某种映射统一起来:
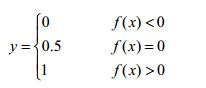
即预测值f(x)>0,label=1;f(x)<0,label=0;这个函数是我们常见的阶跃函数(0.5视为过渡值,这是与单位阶跃函数的唯一区别)。
这个函数可以对我们的计算结果进行分类,但是这个函数非凸非连续,数学性质较差。因此我们可以考虑定义一个与阶跃函数类似,但是既凸又连续的函数。这个函数自然就是我们的sigmoid函数,其定义形式如下:
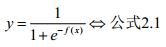
Sigmoid函数与单位阶跃函数的曲线如图2.1所示:

图2.1
对公式2.1进行推演:
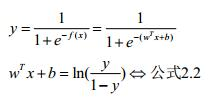
观察公式2.2的对数内部的分数我们容易发现,y与1-y具有很好的性质,即类别上的互补。换句话说,当wTx+b的结果出来之后,我们容易算出右边的对数值只要评定该对数值与0的大小,我们即可进行分类。甚而至于,我们可以将右边对数值视为概率的比值,即wTx+b的结果更倾向于我们将x分入到哪一类。这里开始等价于我们引入了统计机器学习的知识。
我们可将y视为类后验概率密度P(y=1|x),1-y则视为类后验概率密度P(y=0|x)。2.2式可继续推演:
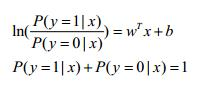
可以解得:
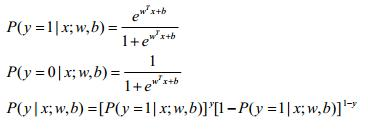
联合概率密度为:
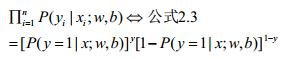
不要忘记,跟线性模型一样,logistic回归在做分类问题,那么一样的需要对数据训练,得到我们最优(或者较优)的模型。也就是我们需要求出w、b这俩参数。我们可以用最大似然法来对w、b的参数进行估计。在这里举个栗子来说明下最大似然法为什么可以对w、b进行参数估计。
栗子:某个男人不幸患了肺癌,现在我毫无征兆的让你判断这个男人是否抽烟,只有是和否没其他答案?我相信只要是个正常人,都会判断这个男人是抽烟的。这其实就是频率学派的最大似然原理。因为我们只有判断这个男人抽烟才能使“该男人患肺癌”这一事件发生的可能性更大。
同样的道理,对公式2.3也是一样的道理。当训练集被采集出来打上label之后,从我们的角度来讲,我们只有使2.3(即x属于其真实label的概率)越高,我们才能达到更好的泛化能力,即通过2.3最大来求w、b。假如2.3很小,即原样本标记就出错了,那么我们也就没有建模的必要了。
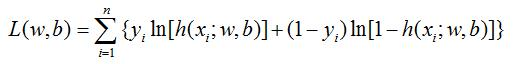
采用梯度下降算法可以求解出w、b。
3.4 线性判别分析
在分类器的理论中,贝叶斯分类器是最优的分类器,而为了得到最优的分类器,我们就需要知道类别的后验概率P(Ck|x)P(Ck|x)。
这里假设fk(x)fk(x)是类别CkCk的类条件概率密度函数,πkπk 是类别CkCk的先验概率,毫无疑问有∑kπk=1∑kπk=1。根据贝叶斯理论有:
P(Ck|x)=fk(x)πk∑Kl=1fl(x)πl
P(Ck|x)=fk(x)πk∑l=1Kfl(x)πl
由于πkπk 几乎是已知的,所以对于贝叶斯公式而言,最重要的就是这个类条件概率密度函数fk(x)fk(x),很多算法之所以不同,主要的就是对这个类条件概率密度函数的参数形式的假设不同,比如:
线性判别分析(LDA)假设fk(x)fk(x)是均值不同,方差相同的高斯分布
二次判别分析(QDA)假设fk(x)fk(x)是均值不同,方差也不同的高斯分布
高斯混合模型(GMM)假设fk(x)fk(x)是不同的高斯分布的组合
很多非参数方法假设fk(x)fk(x)是参数的密度函数,比如直方图
朴素贝叶斯假设fk(x)fk(x)是CkCk边缘密度函数,即类别之间是独立同分布的
各种算法的不同,基本上都是来至于对类条件概率密度函数的不同,这一点在研究分类算法的时候,一定要铭记在心。
前面已经说过了LDA假设fk(x)fk(x)是均值不同,方差相同的高斯分布,所以其类条件概率密度函数可以写为:
fk(x)=1(2π)p/2|Σ|1/2exp(−12(x−μk)TΣ−1(x−μk))
fk(x)=1(2π)p/2|Σ|1/2exp(−12(x−μk)TΣ−1(x−μk))
这里,特征xx的维度为pp维,类别CkCk的均值为μkμk,所有类别的方差为ΣΣ。
在前面提到过,一个线性分类器,在判别式函数δk(x)δk(x)或者后验概率函数P(Ck|x)P(Ck|x)上加上一个单调函数f(⋅)f(⋅)后,可以得变换后的函数是xx的线性函数,而得到的线性函数就是决策面。LDA所采用的单调变换函数f(⋅)f(⋅)和前面提到的Logistics Regression采用的单调变换函数一样,都是logit 函数:log[p/(1−p)]log[p/(1−p)],对于二分类问题有:
logP(C1|x)P(C2|x)=logf1(x)f2(x)+logπ1π2=xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2
logP(C1|x)P(C2|x)=logf1(x)f2(x)+logπ1π2=xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2
可以看出,其决策面是一个平面。
根据上面的式子,也可以很容易得到LDA的决策函数是:
δk(x)=xTΣ−1μk−12μTkΣ−1μk+logπk
δk(x)=xTΣ−1μk−12μkTΣ−1μk+logπk
其中的参数都是从数据中估计出来的:
πk=Nk/Nπk=Nk/N,NkNk是类别CkCk的样本数,NN是总的样本数。
μk=1Nk∑x∈Ckxμk=1Nk∑x∈Ckx ,就是类别CkCk的样本均值
Σ=1N−K∑Kk=1∑x∈Ck(x−μk)(x−μk)TΣ=1N−K∑k=1K∑x∈Ck(x−μk)(x−μk)T
二次判别分析QDA
二次判别函数假设fk(x)fk(x)是均值不同,方差也不同的高斯分布,和LDA相比,由于ΣkΣk是不一样 ,所以其二次项存在,故其决策面为:
logP(C1|x)P(C2|x)=logf1(x)f2(x)+logπ1π2=xT(Σ−11−Σ−12)x+xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2−12log|Σ1||Σ2|
logP(C1|x)P(C2|x)=logf1(x)f2(x)+logπ1π2=xT(Σ1−1−Σ2−1)x+xTΣ−1(μ1−μ2)−12(μ1+μ2)TΣ−1(μ1−μ2)+logπ1π2−12log|Σ1||Σ2|
其对应的判别函数为:
δk(x)=−12(x−μk)TΣ−1(x−μk)−12log|Σk|+logπk
δk(x)=−12(x−μk)TΣ−1(x−μk)−12log|Σk|+logπk
下面这份代码是LDA和QDA的测试代码:
# -*- coding: utf-8 -*-
"""
@author: [email protected]
@time: 2015-07-09_16-01
线性判别式分析示例代码
"""
print __doc__
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import colors
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
##########################################################
# 颜色设置
cmap = colors.LinearSegmentedColormap(
'red_blue_classes',
{
'red': [(0, 1, 1), (1, 0.7, 0.7)],
'green': [(0, 0.7, 0.7), (1, 0.7, 0.7)],
'blue': [(0, 0.7, 0.7), (1, 1, 1)]
}
)
plt.cm.register_cmap(cmap=cmap)
###########################################################
# 生成数据
def dataset_fixed_cov():
'''产生两个拥有相同方差的高斯样本集合'''
n, dim = 300, 2 # 样本数目为300,特征维度为2
np.random.seed(0)
c = np.array([[0, -0.23], [0.83, 0.23]]) #高斯分布的方差
X = np.r_[np.dot(np.random.randn(n, dim), c),
np.dot(np.random.randn(n, dim), c) + np.array([1, 1])]
y = np.hstack((np.zeros(n), np.ones(n)))
return X, y
def dataset_cov():
'''产生两个拥有不同的方差的高斯样本集合'''
n, dim = 300, 2
np.random.seed(0)
c = np.array([[0.1, -1.0], [2.5, 0.7]]) * 2.0
X = np.r_[np.dot(np.random.randn(n, dim), c),
np.dot(np.random.randn(n, dim), c.T) + np.array([1, 4])]
y = np.hstack((np.zeros(n), np.ones(n)))
return X, y
#########################################################################
# 绘图函数
def plot_data(lda, X, y, y_pred, fig_index):
splot = plt.subplot(2, 2, fig_index)
if fig_index == 1:
plt.title('Linear Discriminant Analysis')
plt.ylabel('Data with fixed covariance')
elif fig_index == 2:
plt.title('Quadratic Discriminant Analysis')
elif fig_index == 3:
plt.ylabel('Data with varying covariances')
tp = (y == y_pred) #正样本中,分类正确的数目
tp0, tp1 = tp[y == 0], tp[y == 1]
X0 , X1 = X[y == 0], X[y == 1]
X0_tp, X0_fp = X0[tp0], X0[~tp0]
X1_tp, X1_fp = X1[tp1], X1[~tp1]
# 类别0分类正确的点和分类错误的点
plt.plot(X0_tp[:, 0], X0_tp[:, 1], 'o', color='red')
plt.plot(X0_fp[:, 0], X0_fp[:, 1], '.', color='#990000')
# 类别1分类正确的点和分类错误的点
plt.plot(X1_tp[:, 0], X1_tp[:, 1], 'o', color='blue')
plt.plot(X1_fp[:, 0], X1_fp[:, 1], '.', color='#000099')
# 类别0和类别1的区域
nx, ny = 200, 100
x_min, x_max = plt.xlim()
y_min, y_max = plt.ylim()
xx, yy = np.meshgrid(np.linspace(x_min, x_max, nx),
np.linspace(y_min, y_max, ny))
# 求出LDA的概率分布
z = lda.predict_proba(np.c_[xx.ravel(), yy.ravel()])
z = z[:, 1].reshape(xx.shape)
plt.pcolormesh(xx, yy, z,
cmap='red_blue_classes',
norm=colors.Normalize(0., 1.))
# 这里的等高线,就是对应的决策面
# LDA的决策面是直线,而QDA的决策面是二次曲线
# 注意图中右下角那张图,途中的决策面是双曲线
# 为了更清楚的看出其为双曲线,可以去掉后面两行代码的注释
plt.contour(xx, yy, z, [0.5], linewidths=2., colors='k')
#plt.contour(xx, yy, z, [0.4, 0.6], linewidths=2., colors='g')
#plt.contour(xx, yy, z, [0.3, 0.7], linewidths=2., colors='b')
# 类别0和类别1的中心点
plt.plot(lda.means_[0][0], lda.means_[0][1],
'o', color='k', markersize=10)
plt.plot(lda.means_[1][0], lda.means_[1][2],
'o', color='k', markersize=10)
for i, (X, y) in enumerate([dataset_fixed_cov(), dataset_cov()]):
print i
# 线性判别式分析
lda = LinearDiscriminantAnalysis(solver='svd', store_covariance=True)
y_pred = lda.fit(X, y).predict(X)
splot = plot_data(lda, X, y, y_pred, fig_index=2 * i + 1)
plt.axis('tight')
# 二次判别分析
qda = QuadraticDiscriminantAnalysis(store_covariances=True)
y_pred = qda.fit(X, y).predict(X)
splot = plot_data(qda, X, y, y_pred, fig_index= 2 * i + 2)
plt.axis('tight')
plt.show()
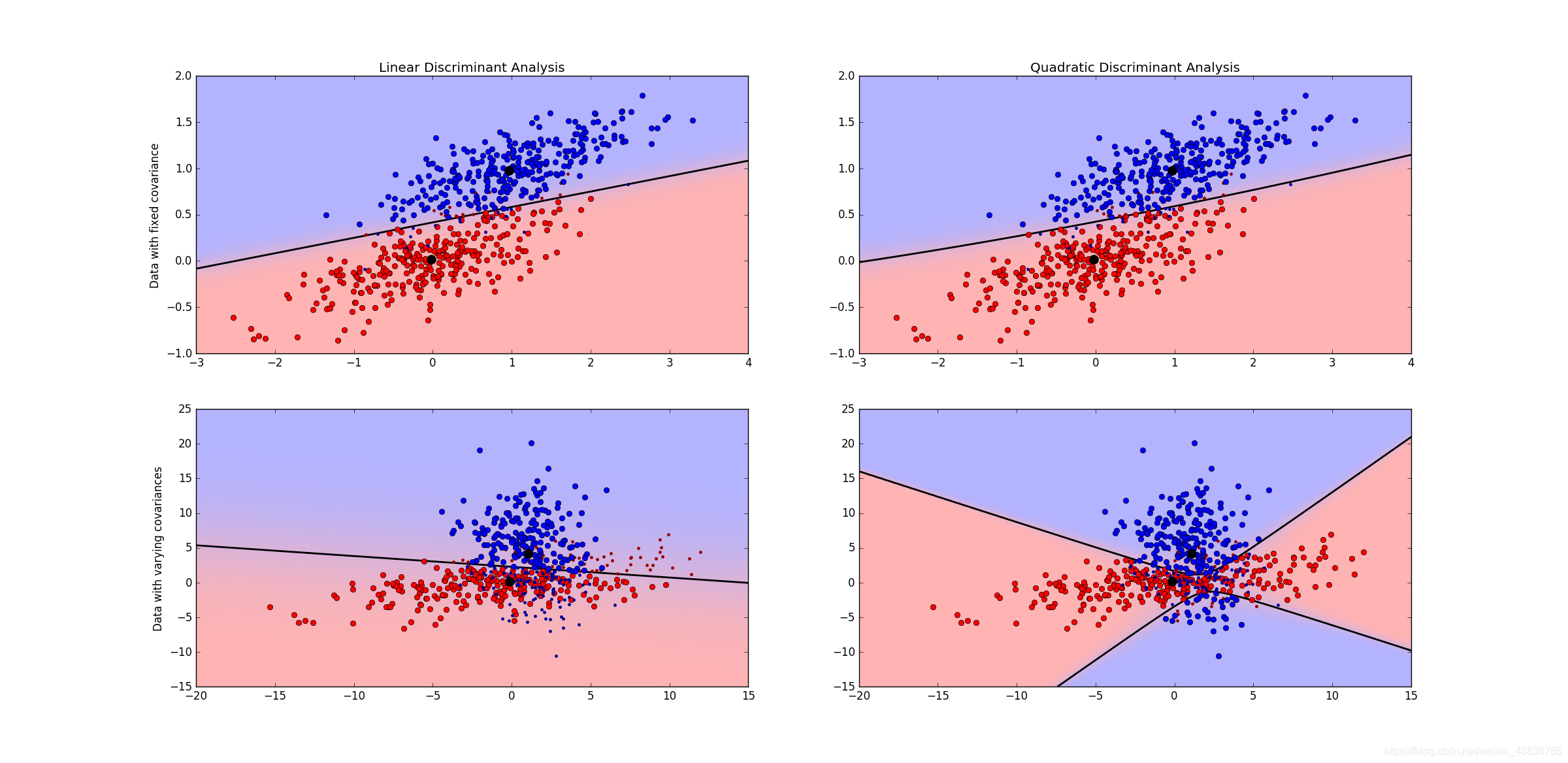
上面两幅图的数据是均值不同,方差相同的数据分布,LDA和QDA都得到一个线性的决策面。下面两幅图是均值和方差都不一样的数据分布,LDA得到一个线性决策面,但是QDA得到的决策面试一个双曲面,注意这里是一个双曲面,并不是两条直线。为了更好的看出其为双曲面,可以将代码中有两行等高线的代码注释去掉,就可以清晰的看出其决策面是双曲线了。
3.5 多分类学习
现实中常遇到多份类任务,有些二分类学习方法可直接推广到多分类,
但在更多情形下,我们是基于一些基本策略,利用二分类学习器来解决多分类问题。
多分类学习的基本思路是“拆解法”,既将多分类任务拆为若干个二分类任务求解。具体地说,先对问题进行拆分,然后为拆出的每一个二分类任务训练一个分类器;在测试时,对这些分类器的预测结果进行集成以获得最终的多分类结果。这里的关键是如何对多分类任务进行拆分,以及如何对多个分类器进行集成。
最经典的拆分策略有三种:
一对一(OvO)
一对多(OvR)
多对多(MvM)
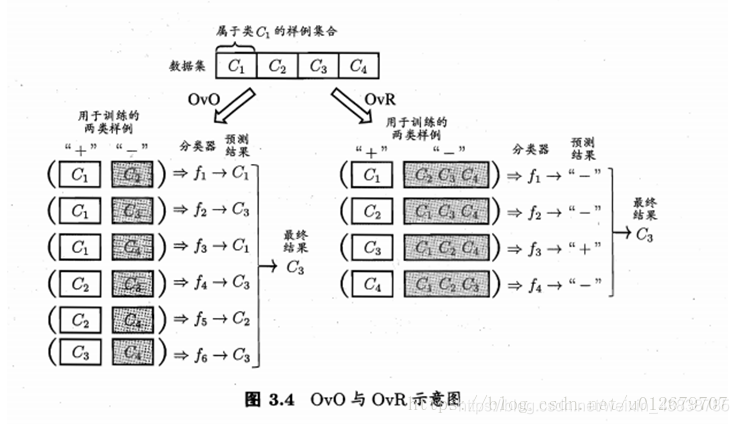
OvO和OvR有何优缺点?
容易看出,OvR只需训练N个分类器,而OvO需训练N(N - 1)/2个分类器, 因此,OvO的存储开销和测试时间开销通常比OvR更大。但在训练时,OvR的每个分类器均使用全部训练样例,而OvO的每个分类器仅用到两个类的样例,因此,在类别很多时,OvO的训练时间开销通常比OvR更小。至于预测性能,则取决于具体的数据分布,在多数情形下两者差不多。
综上:
OvO的优点是,在类别很多时,训练时间要比OvR少。缺点是,分类器个数多。
OvR的优点是,分类器个数少,存储开销和测试时间比OvO少。缺点是,类别很多时,训练时间长。
MvM
MvM是每次将若干个类作为正类,若干个其他类作为反类。显然,OvO和OvR是MvM的特例。MvM的正、反类构造必须有特殊的设计,不能随意选取。这里我们介绍一种最常用的MvM技术"纠错输出码" (Error CorrectingOutputCodes,简称 ECOC)
ECOC是将编码的思想引入类别拆分,并尽可能在解码过程中具有容错性。ECOC工作过程主要分为两步:
----编码:对N个类别做M次划分,每次划分将一部分类别划为正类,一部分划为反类,从而形成一个二分类训练集。这样一共产生M个训练集,可训练出M个分类器。
----解码:M 个分类器分别对测试样本进行预测,这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较,返回其中距离最小的类别作为最终预测结果。
3.6 类别不平衡问题
前面介绍的分类学习中都有一个共同的基本假设,既不同类别的训练样例数目相当,如果不同类别的训练样例数目稍有差别,通常影响不大,但若差别很大,则会对学习过程造成困扰。
解决方法有很多,读者可自行查找,不作重点,因为没人喜欢用这样的数据集,大家可自行查找学习。
就不详细介绍了
PS:大家可以看一下“稀疏表示”,近年来很受关注!
