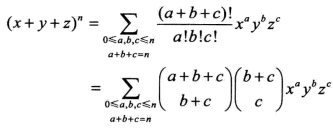又是一大堆公式来袭~~
二项级数的部分和另一种有意思的关系式子:
∑k⩽m(m+rk)xkym−k=∑k≤m(−rk)(−x)k(x+y)m−k,m是整数
当m小于0时,两边均为0;当m=0时,两边都是1。
令左边部分为Sm,右边部分为Tm
Sm=∑k≤m(m−1+rk)xkym−k+∑k⩽m(m−1+rk−1)xkym−k
其中,
∑k⩽m(m−1+rk)xkym−k=(m−1+rm)xm+∑k⩽m−1(m+1+rk)xkym−k=ySm−1+(m−1+rm)xm
∑k≤m(m−1+rk−1)xkym−k=x∑k≤m(m−1+rk−1)xk−1y(m−1)−(k−1)=xSm−1
因此,
Sm=(x+y)Sm−1+(−rm)(−x)m

因此,可证明Sm和Tm是相等的!
∑k⩽m(m+rk)(−1)k=(−rm),整数
m⩾0
相当于(5.16)
(rm)(mk)=(rk)(r−km−k),m,k是整数
(rm)(mk)=m!(r−m)!r!k!(m−k)!m!=k!(m−k)!(r−m)!r!=k!(r−k)!r!k!(r−k)!(r−k)!(m−k)!(r−m)!(r−k)!=(rk)(r−km−k)
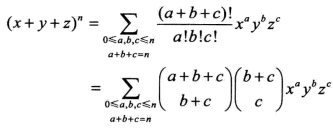
(a+b+ca,b,c)=a!b!c!(a+b+c)!
多项式系数:
(a1+a2+⋯+ama1,a2,⋯,am)=a1!a2!⋯am!(a1+a2+⋯+am)!
=(a1+a2+⋯+am!a2+⋯+am)⋅(am−1+amam)

例子:
∑k(rm+k)(sn−k)
令
k1=m+k
=
∑k1−m(rk1)(sn+m+k1)=
∑k1−m(rk1)(Sn−(k1−m))
令
K2=n−k
∑n−k2(rm+n−k2)(Sk2)
上述表中的式子根本记不住的,其实就是范德蒙德卷积:
∑k(rk)(sn−k)=(r+sn),n是整数