本章讲述的是二项式系数,包含了一大堆记不住的公式@<@
1.
(rk)={k(k−1)⋯(1)r(r−1)⋯(r−k+1)=k!rk,k⩾00,k<0
当k=0时,上述结果为1
r为上指标,k为下指标,表示从r个数里面取k个的排序
2.帕斯卡三角形(杨辉三角形)
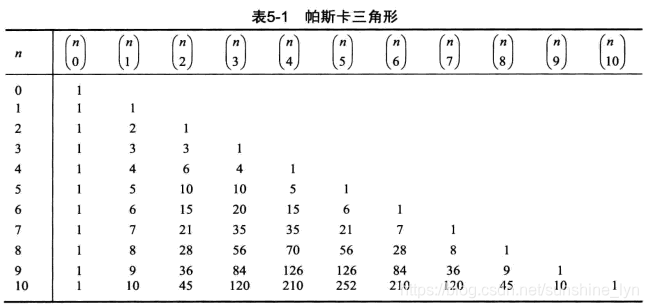
(r0)=1,(r1)=r,(r2)=2r(r−1)
☆ 考虑式子
(−1k)=?(−1−1−k)
(−1k)=k!(−1)(−2)⋯(−k)=(−1)k
(−1−1−k)=(−1)−1−k(由上式可以得出),它是1或者-1
因此上述等式总是相等是错误的!
3.吸收等式(5.5)
(rk)=kr(r−1k−1),
整数k̸=0
4.相伴恒等式(5.7)
(r−k)(rk)=r(r−1k)
(r−k)(rk)=(r−k)(rr−k),对称性=r(r−1r−k−1),吸收等式=r(r−1k),对称性
5.加法公式(杨辉三角的性质)(5.8)
(rk)=(r−1k)+(r−1k−1),k是整数
利用定义证明:
∑k⩽n(r+kk)=(r0)+(r+11)+⋯+(r+nn)
=(r+n+1n),n是整数
6.关于上指标求和
∑0⩽k⩽n(km)=(0m)+(1m)+⋯+(nm)
=(n+1m+1),整数
m,n⩾0
k≤n∑(m+kk)=−m≤k⩽n∑(m+kk)=−m≤k⩽n∑(m+km)=0⩽k⩽m+n∑(km)=(m+n+1m+1)=(m+n+1n)
7.上指标反转(5.14)
(rk)=(−1)k(k−r−1k),k是整数
8.
(−1)m(−n−1m)=(−1)n(−m−1n)
=(m+nn),整数
m,n⩾0
利用上指标公式,也可以推导出下列式子(帕斯卡三角形一行的部分交替求和):
∑k≤m(rk)(−1)k=(r0)−(r1)+⋯+(−1)m(rm)
=(−1)m(r−1m),m是整数
k⩽m∑(rk)(−1)k=k⩽m∑(k−r−1k)=(−r+mm)=(−1)m(r−1m)

