共轭梯度

共轭梯度法

问题

依旧是运用变分法求解线性方程组 $Ax = b$

与最速下降的区别

共轭梯度与最速下降的区别在于共轭梯度在下降方向的选取上，要求下一次下降的方向与上一次的方向关于系数矩阵A是共轭的关系。

为何要这样进行优化，是因为如果我们选择d为下降的初始方向，那么对于n维度正定实对称系数矩阵A来说，与d关于A共轭的方向最多只有n-1个，我们可以将之理解为另一种形式的正交。

由此，我们认为如果没有计算误差的理想情况下，运用共轭梯度法我们只用进行n次下降就能达到方程的解的位置

可视化

我们接着这个专栏进行下去，始终用的是MATLAB
对问题的描述：传送门： [link]（https://blog.csdn.net/weixin_29732003/article/details/103310961）

clear
clc
%% 参数
N = 3;%图像宽度
X0 = [-0.5;-0.5];%迭代初值
e0 = eps;%torlation
%方程
A = [3 1;1 5];
b = [1;1];
%% 表达式以及网格化表面图
figure(1)
vec = -N/2+0.5:0.01:N/2-0.5;
[xx, yy] = meshgrid(vec,vec);
T = [xx, yy];
Z = 0.5*(3*xx.^2+2*xx.*yy+5*yy.^2)-xx-yy;
s = surf(xx,yy,Z,'FaceAlpha',0.5,'EdgeColor','none');
colorbar
%% 等高线图
figure(2);
subplot(1,2,1);
contour(xx,yy,Z);  %绘制函数的等高线
subplot(1,2,2);
contourf(xx,yy,Z,16);  %绘制等高线指定条数16并填充颜色
%% 最速下降
figure(3)
surf(xx,yy,Z,'FaceAlpha',0.5,'EdgeColor','none')
hold on
%开始求解
X = X0;
r = A*X - b;
%开始迭代
while(abs(r)>e0)
    % alpha 是每次迭代的步长
    alpha = (r.*r)/(r'*A*r);
    Xp = X;
    X = X - alpha.*r;
    P1 = linspace(Xp(1),X(1));
    P2 = linspace(Xp(2),X(2));
    T = 0.5*(3*P1.^2+2*P1.*P2+5*P2.^2)-P1-P2;
    plot3(P1,P2,T,'Color','r','LineWidth',1)
    hold on
    r = A*X - b;
end
hold off
%% 最速下降等高线图
figure(4)
axis equal
contour(xx,yy,Z,20)
hold on
%开始求解
X = X0;
r = A*X - b;
k = 0;
%开始迭代
while(norm(r)>e0)
    % alpha 是每次迭代的步长
    alpha = (r.*r)/(r'*A*r);
    Xp = X;
    X = X - alpha.*r;
    P1 = linspace(Xp(1),X(1));
    P2 = linspace(Xp(2),X(2));
    plot(P1,P2,'Color','r','LineWidth',1)
    hold on
    Pu1 = [Xp(1),X(1)];
    Pu2 = [Xp(2),X(2)];
    [pt1, pt2] = meshgrid(Pu1,Pu2);
    Zu = 0.5*(3*pt1.^2+2*pt1.*pt2+5*pt2.^2)-pt1-pt2;
    contour(pt1-(X(1)-Xp(1))/2,pt2-(X(2)-Xp(2))/2,Zu,1)
    r = A*X - b;
    k = k+1;
end
%% 共轭梯度
figure(5)
surf(xx,yy,Z,'FaceAlpha',0.5,'EdgeColor','none')
hold on
X = X0;
% r 为剩余向量
r = b-A*X;
% d 为下降方向
% 第0 步的下降方向为负的梯度方向
d = r;
%更新第0步的步长
alpha = (r.*d)/(d'*A*d);
%完成第一次迭代
X = X + alpha.*d;
%计数器
kc = 1;
%以后的搜索方向都是共轭的方向
while(norm(r)>e0)
    %更新新的梯度方向
    r = b-A*X;
    %更新方向
    %更新上一次的方向在这一次方向的表达式上的系数
    beta = -(r'*A*d)/(d'*A*d);%这里的d是上一次的下降方向
    d = r + beta.*d;
    %方向上的更新完成
    %更新步长
    alpha = (r.*d)/(d'*A*d);
    Xp = X;
    X = X + alpha.*d;
    P1 = linspace(Xp(1),X(1));
    P2 = linspace(Xp(2),X(2));
    T = 0.5*(3*P1.^2+2*P1.*P2+5*P2.^2)-P1-P2;
    plot3(P1,P2,T,'Color','r','LineWidth',1)
    hold on
    kc = kc+1;
end
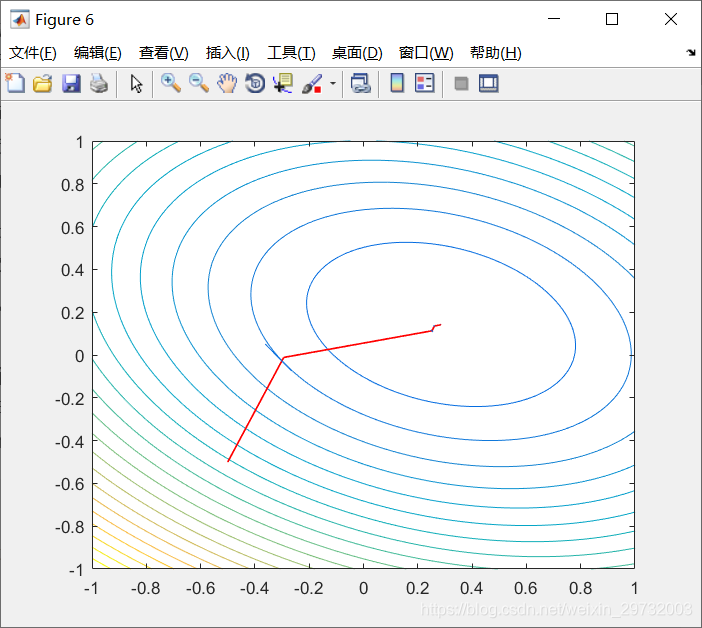
%% 共轭梯度等高线图
figure(6)
contour(xx,yy,Z,20)
hold on
X = X0;
% r 为剩余向量
r = b-A*X;
% d 为下降方向
% 第0 步的下降方向为负的梯度方向
d = r;
%更新第0步的步长
alpha = (r.*d)/(d'*A*d);
Xp = X;
%完成第一次迭代
X = X + alpha.*d;
P1 = linspace(Xp(1),X(1));
P2 = linspace(Xp(2),X(2));
plot(P1,P2,'Color','r','LineWidth',1)
hold on
%计数器
kc = 1;
%以后的搜索方向都是共轭的方向
while(norm(r)>e0)
    %更新新的梯度方向
    r = b-A*X;
    %更新方向
    %更新上一次的方向在这一次方向的表达式上的系数
    beta = -(r'*A*d)/(d'*A*d);%这里的d是上一次的下降方向
    d = r + beta.*d;
    %方向上的更新完成
    %更新步长
    alpha = (r.*d)/(d'*A*d);
    Xp = X;
    X = X + alpha.*d;
    P1 = linspace(Xp(1),X(1));
    P2 = linspace(Xp(2),X(2));
    plot(P1,P2,'Color','r','LineWidth',1)
    hold on
    Pu1 = [Xp(1),X(1)];
    Pu2 = [Xp(2),X(2)];
    [pt1, pt2] = meshgrid(Pu1,Pu2);
    Zu = 0.5*(3*pt1.^2+2*pt1.*pt2+5*pt2.^2)-pt1-pt2;
    contour(pt1-(X(1)-Xp(1))/2,pt2-(X(2)-Xp(2))/2,Zu,1)
    kc = kc+1;
end

图如下