《共轭梯度法》读书笔记（二）——共轭方向法

最速下降法的缺陷

上一节中已经提到了最速下降法容易走出“之”字形的路线，这些路线方向虽然都是梯度，但非常类似。如果每次的路线都是彼此正交的，那么即使没有选择局部变化率最大的梯度，也能够很快收敛到正解，如下图。

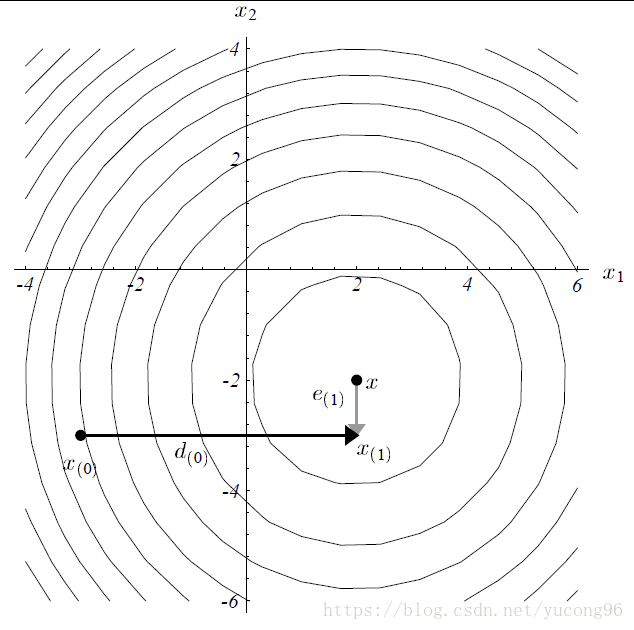
共轭方向法的intuition

这就引出了共轭方向法 (Conjugate Directions)。

一种理想但无法实现的共轭梯度法

我们选择一组正交的搜索方向，记为$d_j(j=1...n)$，每次迭代时，仅在一个$d_j$方向上迭代，即

$$x_{(i+1)} = x_{(i)} + \alpha d_i$$

我们希望一次迭代完后，以后的迭代再也不需要在$d_i$方向上修正了，因此，我们希望$d_i^T e_{(i+1)} = 0$，继续计算，得到

$$d_i^T (e_{(i)} + \alpha d_i) = 0 \\ \alpha = - \frac{d_i^T e_{(i)}}{d_i^T d_i}$$

然而，这种算法是不可能的，因为$e_{(i)}$是未知量（假如我们知道了$e_{(i)}$，那正解也就得到了），$\alpha$无法因此求出。

修正

与之前选择一组正交基相比，这里我们选择一组基于矩阵A的A正交基，记为$d_j(j=1...n)$，即$d_i^TAd_j=0 ( i \ne j)$。下图可以直观地看到A正交基的样子，虽然它们不正交，但如果A变换为单位阵，则它们就可以正交了（见下右图）。

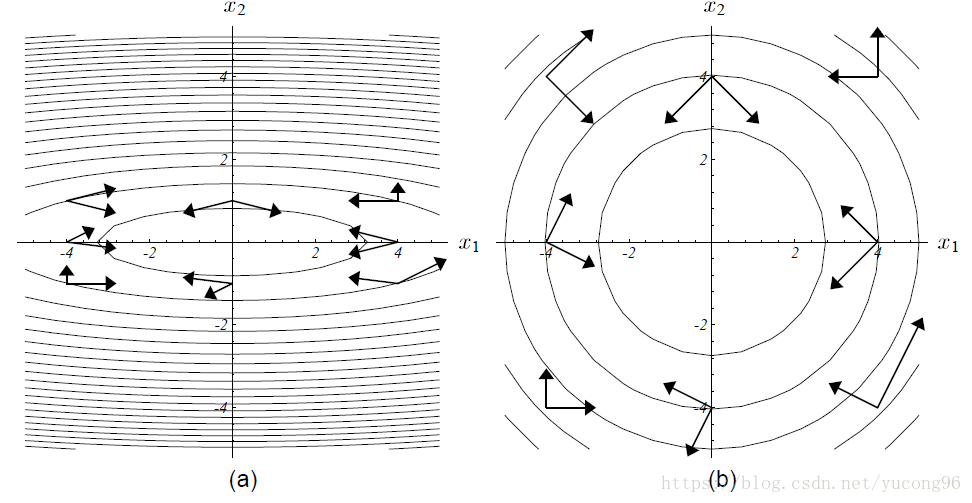
A正交基

类似的，我们求解$d_i^T A e_{(i+1)}= 0$，继续计算，得到

$$d_i^T A (e_{(i)} + \alpha d_i) = 0 \\ - d_i^T r_{(i)} + \alpha d_i^T A d_i = 0 \\ \alpha = \frac{d_i^T r_{(i)}}{d_i^T A d_i}$$

注意到，如果把$d_i$替换为$r_{(i)}$，那么$\alpha$的表达式将和最速下降法是一致的，这表明共轭方向法也是在$d_i$的方向上找到了一个最小值。这是符合我们预期的。
共轭方向法的收敛性证明比较简单，因为一共$n$个方向，每次都消除了一个方向上的误差，经过$n$轮迭代，就一定可以得到正解。
类似最速下降法，通过对残差的迭代，可以加速迭代过程，即

$$r_{(i+1)} = -Ae_{(i+1)} = -A(e_{(i)} + \alpha d_i) = r_{(i)} - \alpha A d_i$$

寻找一组A正交基

假设我们已经有了一组线性无关的向量，记为$u_1,...,u_n$，那么使用施密特正交化法 (Gram-Schmidt Conjugation)，就能得到一组正交基作为下降方向$d_1,...,d_n$。过程如下，首先$d_1=u_1$，然后对于$d_i$，有

$$d_i = u_i - \sum_{k=1}^{i-1} \beta_{ik} d_k$$

由于$d_i$和任一$d_j (j \ne i)$均正交，因此

$$d_i^T A d_j = u_i^T A d_j - \sum_{k=1}^{i-1} \beta_{ik} d_k^T A d_j \\ 0 = u_i^T A d_j - \beta_{ij} d_j^T A d_j \\ \beta = \frac{u_i^T A d_j}{d_j^T A d_j}$$

缺陷

虽然共轭梯度法只需要$n$步就能保证收敛，但单次迭代有时会非常耗时（主要是使用施密特正交化法），因此它并不太使用。一个例子是，假如我们取坐标轴作为一组正交基执行共轭方向法，那么每次消去一个方向上的误差和高斯消元法是完全一致的。

参考文献

• 《An Introduction to the Conjugate Gradient Method Without the Agonizing Pain》